次： 円周率を表す 上： 素数の分布 前： 素数分布の探求

素数定理

南海　　 定理8は定理7の(2)の別証明になっている．

拓生　

$$\dfrac{c_1}{\log x}<\dfrac{\pi(x)}{x}<\dfrac{c_2}{\log x}$$

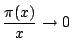ですから，$x\to \infty$のとき，はさみうちの原理によって $\dfrac{\pi(x)}{x}\to 0$である．

南海　　 チェビシェフはさらにこの$c_1,\ c_2$を調べ，

$$0．92\dfrac{x}{\log x}<\pi(x)<1.11\dfrac{x}{\log x}$$

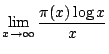まで示した．またもし $$\lim_{x \to \infty}\dfrac{\pi(x)\log x}{x}$$が収束するならば， それは1であることも示した．

チェビシェフのこの証明からさらの半世紀後，1896年になってフランスの数学者アダマール(J.Hadamard)と プーサン(C.de la Vallée Poussin)によってほとんど同時に独立に

$$\lim_{x \to \infty}\dfrac{\pi(x)\log x}{x}=1$$

が示されたのだ．これを素数定理という． 彼らの方法はリーマンの$\zeta$関数を用いるきわめて難しいものだった． 1949年になってセルバーグ(A.Selberg)が$\zeta$関数を用いない初等的な方法で示した．

素数については今日もまだ未解決な問題がたくさんある．この世界に素数があるということは なんと不思議なことなのだろう．

さて，青空学園では2005年〜2007年に数論の読者会をした．そこで，私が『解析的整数論』(末綱恕一，岩波書店)に載っている素数定理の証明を紹介した．読書会に使った『数論I』の定理7.3 までは用いる．その他は出来るかぎり完結的に整理した．といっても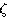， 関数を中心に複素関数論を使うので，理解は難しい．あくまで参考にするということで，それをここに紹介する．