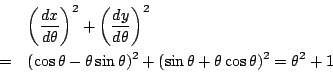次: 惑星は楕円軌道を描く
上: 懸垂線と双曲線
前: 双曲線関数の逆関数
耕一
これはまさに放物線の弧長の式です.
放物線
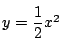 の
の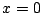 から
から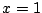 の部分の長さは,
の部分の長さは,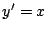 なので,
なので,
です.ところが上の不定積分があるので,
と求まります.
南海
渦巻き線
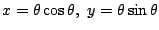 の
の
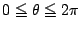 の
部分の長さを求めようとすると,次の計算が必要である.
の
部分の長さを求めようとすると,次の計算が必要である.
したがってこの長さは
となり,同じ不定積分が必要になる.これは2002年京大で出題された.
紹介しておこう.
放物線を頂点で軸と直交する直線に沿ってすべらないように転がすとき,焦点のえがく軌跡が懸垂線になる.これをあつかった入試問題を,
途中の小問をすべて省いて紹介する.これまで導いた式を使って解いてみよう.
演習追加 [98早稲田理工改題] 解答
Aozora Gakuen
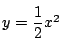 の
の![]() の
の
![]() の
部分の長さを求めようとすると,次の計算が必要である.
の
部分の長さを求めようとすると,次の計算が必要である.