史織
はい.区間 ![]() で連続で区間
で連続で区間 ![]() で微分可能な関数
で微分可能な関数 ![]() に対して
に対して
![]() の
の ![]() で
で
南海
これから分母を払って整理すると
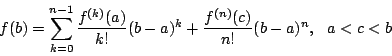
証明
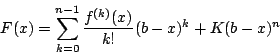
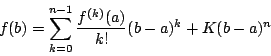
よって, ロルの定理により ![]() である
である ![]() が存在して,
が存在して,
![]() となる. ここで
となる. ここで
![\begin{displaymath}
F'(x)=
\sum^{n-1}_{k=0}
\left[\dfrac{f^{(k+1)}(x)}{k!}(b-x)^k-\dfrac{f^{(k)}(x)}{k!}k(b-x)^{k-1}\right]
-Kn(b-x)^{n-1}
\end{displaymath}](images/img158.png)
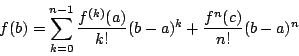
史織 平均値の定理の証明と似ています.
南海
そう.うまく関数 ![]() をとりロルの定理から
をとりロルの定理から ![]() の存在を示すのはまったく同じだ.
の存在を示すのはまったく同じだ.
この定理を![]() で用い,
で用い, ![]() を
を
![]() とあらわすと次のようになる.
とあらわすと次のようになる.
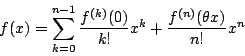
史織
ちょっと待ってください.
![]() のときは,
のときは, ![]() は何回微分しても
は何回微分しても ![]() だから
だから
南海 そうだね.これを題材にした問題は多い.この展開は後にも何度も出てくる
ところで実数 ![]() に対し,
に対し,
![]() で用いるとどうなるかな.
で用いるとどうなるかな.
史織
やってみます. ![]() に対して,
に対して,
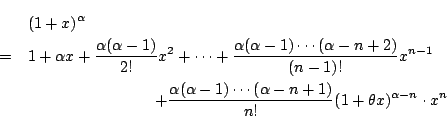
南海
さらに![]() が自然数
が自然数 ![]() の場合は?
の場合は?
史織
![]() が自然数
が自然数 ![]() の場合, 最終項は
の場合, 最終項は
南海 考えてみれば二項定理は多項式の展開法則だから一致するのは当然なのだが, なかなかうまくできている.
さて,本題.![]() が何度でも微分可能とする.
が何度でも微分可能とする.
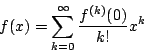
ここで厳密でない論証をしている.どのような ![]() で収束するのか,この展開に対して微分は
各項の微分でいいのか,等々.これは大学数学の課題だ.
で収束するのか,この展開に対して微分は
各項の微分でいいのか,等々.これは大学数学の課題だ.
先の ![]() から作った無限級数
から作った無限級数
同様にして
![]() の展開式を作ってみてほしい.
の展開式を作ってみてほしい.
史織 はい.
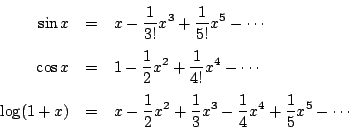
南海
![]() はもちろん
はもちろん ![]() でなければならないが,-1<x≦1の範囲の
でなければならないが,-1<x≦1の範囲の ![]() で収束する.収束範囲については『解析基礎』「級数展開」等を参照.
で収束する.収束範囲については『解析基礎』「級数展開」等を参照.
これは, 数学IIIC の関数の近似で学習した近似式を, 任意の精度で精密化したものである. 最近は近似式が必修でないので習っていないかも知れない.