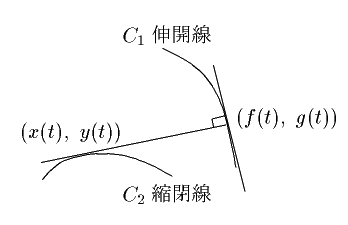
太郎 曲線に巻かれたひもを,まっすぐに伸ばしてゆくとき,その先端の描く曲線が,もとの曲線の伸開線というということを知りました.
図を見ると,伸ばしたひもの先端はその点での伸開線の接線と直交しています. またひもを伸ばした直線は,もとの曲線と接しています.

『数学対話』のなかの「包絡線」 を見ると,逆に,もとの曲線は伸開線の包絡線になっているのですね.
南海
その通りだ.それが縮閉線だ.
平面上の曲線![]() に対し,曲線上の点の法線を考え,
その点が動くとき,その法線の包絡線
に対し,曲線上の点の法線を考え,
その点が動くとき,その法線の包絡線![]() を縮閉線という.
を縮閉線という.
伸開線![]() に対して縮閉線
に対して縮閉線![]() は一意に定まるが,
逆に,同じ縮閉線を作る伸開線は無数にある.
は一意に定まるが,
逆に,同じ縮閉線を作る伸開線は無数にある.
太郎 そうか.ひもの長さを変えると伸開線は変わってくるが, しかし,法線の包絡線は同じですね.
南海 これらの曲線は,いわゆる微分幾何の最初にでてくるものだ. ここでは,高校範囲で考えるため,曲率や曲率半径といった概念なしに考えよう.
『解析基礎』の「微分と幾何」では,これらの定義までは述べた.がそこでは, 「伸開線,縮閉線の話題や,包絡線の一般論などさまざまに論ずべきことがあるが,ここは当初の目的である力学の数学的な基礎部分に絞ってここで終え」た.
そこで,ここでは,媒介変数で表されたいくつかの曲線に対し,その縮閉線を求めよう. つまりその曲線の法線の包絡線を求めよう. それはもとの曲線に対して一意に定まるので,考えやすい.
先の「包絡線」をふりかえる.そこに書かれていることを再構成しよう.
曲線![]() が媒介変数
が媒介変数![]() によって
によって![]() と表されるとする.
この
と表されるとする.
この![]() に対応する,包絡線上の点
に対応する,包絡線上の点![]() とする.
先の図にこれらの点も書き入れる.
とする.
先の図にこれらの点も書き入れる.
このときベクトル
![]() と,
接線方向
と,
接線方向
![]() は直交している.よって,
は直交している.よって,
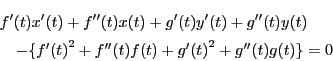
ここで,![]() に対応する法線と
に対応する法線と![]() に対する法線の交点を
に対する法線の交点を![]() とする.
とする.
![]() と比較して,
と比較して,
![]() のとき,
のとき,
![]() となることがわかる.
となることがわかる.
この方法で楕円の縮閉線を求める問題が 98年の慶応医学部 で出題されている.
この慶応の問題を一般化して,2次曲線の縮閉線を考えてゆこう.