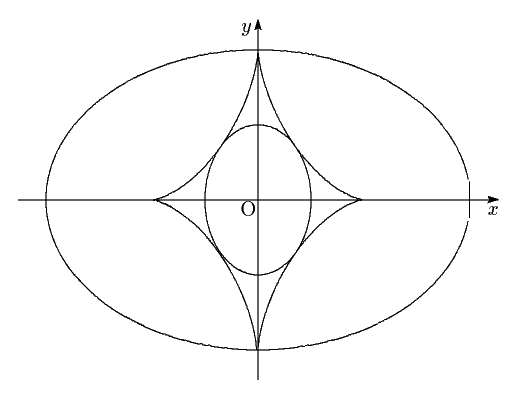
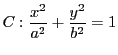 ������D
������D
![]() ��
��![]() ��
��![]() �̐��̒萔�Ƃ���
�̐��̒萔�Ƃ���![]() ���ʏ�ɑȉ~
���ʏ�ɑȉ~
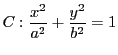 ������D
������D
�ȉ~�̔}��ϐ��\���ł�,�p���K�v�ł���D�����ŁC![]() �̑����
�̑����![]() ��p����D
����ɂ���ċȐ�
��p����D
����ɂ���ċȐ�![]() �́C
�́C
![]() �C
�C
![]() �̔}��ϐ��\�������D
�̔}��ϐ��\�������D
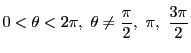 �̂Ƃ��C
�_
�̂Ƃ��C
�_
![]() �ł̖@���̕����������߂�D
�ł̖@���̕����������߂�D
�_
![]() ��
��![]() ��̓_
��̓_
![]() �ɑ��C
����
�ɑ��C
����![]() ���C�_
���C�_![]() �ł�
�ł�![]() �̖@���ł���Ƃ���D
�̖@���ł���Ƃ���D
�_![]() �ł�
�ł�![]() �̐ڐ���
�̐ڐ���
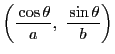 �ł���D
�ł���D
![]() �����̖@�������ƕ��s�ł���̂ŁC
�����̖@�������ƕ��s�ł���̂ŁC
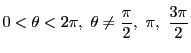 �Ȃ̂ŁC
�Ȃ̂ŁC
���̕�������߂�D
![]() ��̓_
��̓_
![]() �ł̖@�����C���߂����Ɛڂ���_��
�ł̖@�����C���߂����Ɛڂ���_��
![]() �Ƃ���D���̂Ƃ��C
�Ƃ���D���̂Ƃ��C
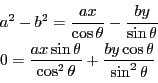
������������D
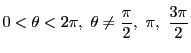 �Ƃ���D
���ʏ�̓_
�Ƃ���D
���ʏ�̓_
![]() ����
����![]() ��̓_
��̓_
![]() �ɏ��Ȃ��Ƃ�4�{�̈قȂ�@����������Ƃ���D
���̂悤�ȓ_
�ɏ��Ȃ��Ƃ�4�{�̈قȂ�@����������Ƃ���D
���̂悤�ȓ_![]() �̏W���́C�s����
�̏W���́C�s����![]() �ŕ\�����̈�ƂȂ�D
�ŕ\�����̈�ƂȂ�D
�ؖ�
![]() �Ƃ���D
���̂Ƃ��C�_
�Ƃ���D
���̂Ƃ��C�_
![]() ��ʂ�@���ƂȂ�
��ʂ�@���ƂȂ�![]() ��̓_��
��̓_��
![]() �Ƃ���ƁC
�Ƃ���ƁC
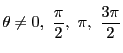 �ł���D
�ł���D
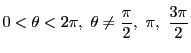 �ɑ��āC
�ɑ��āC
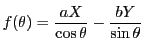 �Ƃ����D
�Ƃ����D
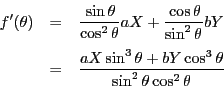
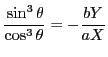 �ƂȂ�Ƃ��C�܂�C
�ƂȂ�Ƃ��C�܂�C
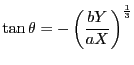 �̂Ƃ��ł���D
�̂Ƃ��ł���D
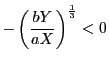 ���C������݂���
���C������݂���![]() �́C
�́C
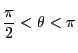 �C
�C
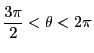 ��1������D
�����
��1������D
�����![]() �C
�C![]() �Ƃ���D
�Ƃ���D
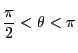 �̂Ƃ��C
�̂Ƃ��C![]() ��
��![]() ����������̂ŁC
����������̂ŁC
![]() ��
��![]() �Ő�����ɕ��ɕς��C
�Ő�����ɕ��ɕς��C![]() �ŋɑ�C
�ŋɑ�C
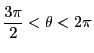 �̂Ƃ��C
�̂Ƃ��C![]() ��
��![]() ����������̂ŁC
����������̂ŁC
![]() ��
��![]() �ŕ����琳�ɕς��C����
�ŕ����琳�ɕς��C����![]() �ŋɏ��ł���D
�ŋɏ��ł���D
���������āC
![]() ���قȂ�4�̉������̂�
���قȂ�4�̉������̂�
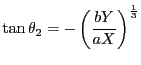 ���C
���C
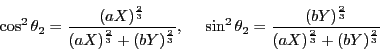
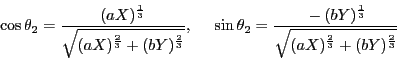
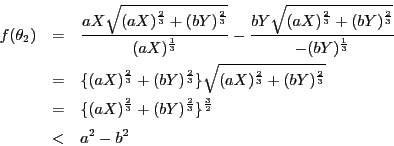
![]() �C
�C![]() �̂����ꂩ�����ł���Ƃ����C�}�`�̑Ώ̐��ƕs�����̑Ώ̐�����C
���l�̊W�����藧�D
�̂����ꂩ�����ł���Ƃ����C�}�`�̑Ώ̐��ƕs�����̑Ώ̐�����C
���l�̊W�����藧�D
![]() �C
�C![]() �̂Ƃ�
�̂Ƃ�
���s����![]() ��
��
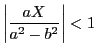 �̂Ƃ��ŁC
���̂Ƃ�����
�̂Ƃ��ŁC
���̂Ƃ�����
![]() �C
�C![]() �̂Ƃ������l�ł���D
�̂Ƃ������l�ł���D
![]() �Ȃ�@����
�Ȃ�@����![]() ����
����![]() ���ɂƂ�C�Ή�����_�͂S����D
���ɂƂ�C�Ή�����_�͂S����D![]() ��
��![]() ���݂����D
���݂����D
�ȏォ��C���ʏ�̓_![]() ���班�Ȃ��Ƃ�4�{�̈قȂ�@����������������C
���班�Ȃ��Ƃ�4�{�̈قȂ�@����������������C
![]() �ł��邱�Ƃ������ꂽ�D
�ł��邱�Ƃ������ꂽ�D
3�{��������������l�Ɏ������D
�֘A������肪2020�N���嗝��6�� �ł���D
6�Ԃł́C�ȉ~��
���̌`�Ɍ��肵���ő�l�Ȃ̂ŁC�����܂ŏ\�������ł����Ȃ��D
![]() �̂Ƃ��̐}�͎��̂悤�ɂȂ�D
�̂Ƃ��̐}�͎��̂悤�ɂȂ�D