

 次: 倍角公式から得られる代数方程式
上: ζを関・ベルヌーイ数で表す
前: ζを関・ベルヌーイ数で表す
次: 倍角公式から得られる代数方程式
上: ζを関・ベルヌーイ数で表す
前: ζを関・ベルヌーイ数で表す
定義 1 (関・ベルヌーイ数)
数列
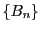
を次の漸化式で定義する.
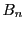
を
関・ベルヌーイ数という.
■
関・ベルヌーイ数は日本の関孝和と,
スイスのヤコブ・ベルヌーイが17世後半にそれぞれ独立に発見した.
数列の性質を調べる強力な手段が母関数の方法である.
一般に,数列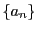 に対して,
形式的なべき級数
に対して,
形式的なべき級数
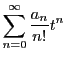 を指数的母関数という.
を指数的母関数という.
関・ベルヌーイ数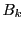 に対して,その指数的母関数を
に対して,その指数的母関数を
とおく.
命題 1
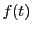
は等式
を満たす.ただし
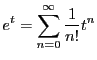
とする.
■
証明
ここで,
であるから,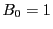 を必要なところに代入して
を必要なところに代入して
これから上記等式が成立する.
□
命題 2
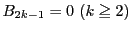
である.
■
証明
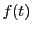 の一次の項は
の一次の項は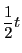 である.
である.
となる.ところが
となり,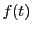 から項
から項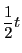 を除いた部分は偶関数である.
従って
を除いた部分は偶関数である.
従って
が示された.
□
定義 2 (ベルヌーイ多項式)
自然数
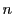
に対して,多項式
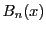
を
関・ベルヌーイ数
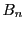
を用いて
で定める.
これを
ベルヌーイ多項式という.
■
定義から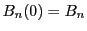 である.基本性質をあげる.2.はあとでは使わないが,
ベルヌーイ多項式の意味そのものなのであげておく.
である.基本性質をあげる.2.はあとでは使わないが,
ベルヌーイ多項式の意味そのものなのであげておく.
証明
1.
命題1と同様の計算を行う.
2.
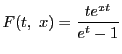 とおく.
二つの変形を行う.
とおく.
二つの変形を行う.
1.を用いて
両辺の級数展開での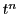 の係数を比較する.
の係数を比較する.
よって,
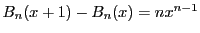 である.
である.
3.
同様に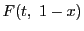 を考える.
を考える.
同様に両辺の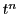 の係数比較から
の係数比較から
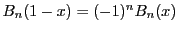 を得る.
□
を得る.
□


 次: 倍角公式から得られる代数方程式
上: ζを関・ベルヌーイ数で表す
前: ζを関・ベルヌーイ数で表す
Aozora
2018-05-14
次: 倍角公式から得られる代数方程式
上: ζを関・ベルヌーイ数で表す
前: ζを関・ベルヌーイ数で表す
Aozora
2018-05-14
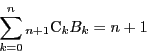
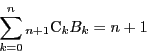
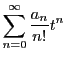 を指数的母関数という.
を指数的母関数という.
![]() に対して,その指数的母関数を
に対して,その指数的母関数を
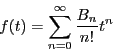
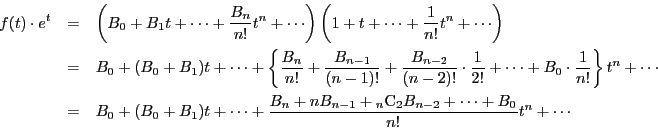
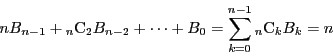

![]() の一次の項は
の一次の項は![]() である.
である.
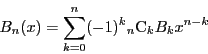
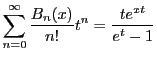 .
.
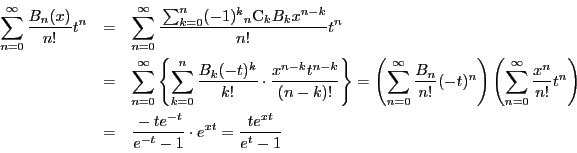
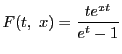 とおく.
二つの変形を行う.
とおく.
二つの変形を行う.
