

 次: 係数定理
上: ζを関・ベルヌーイ数で表す
前: 関・ベルヌーイ数とベルヌーイ多項式
次: 係数定理
上: ζを関・ベルヌーイ数で表す
前: 関・ベルヌーイ数とベルヌーイ多項式
ド・モアブルの定理
の右辺を二項定理で展開し,両辺の虚数部分をとる.
と展開されるので
である.全体を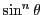 でくくる.
でくくる.
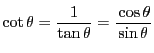 を用いて
を用いて
となる.これは正弦の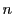 倍角の公式の
倍角の公式の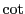 による表現である.
による表現である.
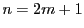 として終項まで書く.
として終項まで書く.
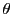 に
に
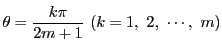 を代入する.
この
を代入する.
この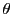 の値に対して
の値に対して
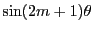 は0で,
は0で,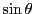 は0でない.
よってこれらの
は0でない.
よってこれらの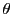 の値に関して
の値に関して
が成り立つ.
つまり
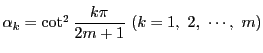 は、
は、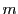 次方程式
次方程式
の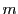 個の相異なる根である.
個の相異なる根である.
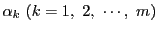 の
の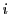 次の基本対称式を
次の基本対称式を
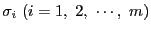 とする.
根と係数の関係式から
とする.
根と係数の関係式から
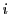 に対して
に対して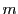 を十分大きくとると
を十分大きくとると
となり,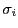 は
は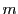 の
の 次多項式で,最高次の係数は
次多項式で,最高次の係数は
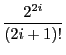 である.
である.
さらに,
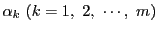 の
の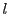 乗和を
乗和を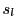 とする.
とする.
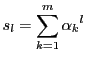 である.
である.
補題 1
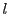
が与えられた自然数,それに対して
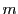
を
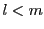
にとる.
が成り立つ.
■
証明
自然数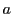 と
と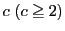 に対して
に対して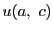 を,
を,
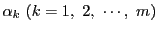 の異なる
の異なる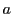 個の積で,
そのうち
個の積で,
そのうち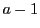 個は一乗,一つが
個は一乗,一つが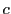 乗であるもの全体の和とする.例えば
乗であるもの全体の和とする.例えば
である.
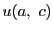 はそれ自身
はそれ自身
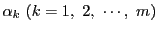 の対称式である.以下,和は異なる添え字にわたるものとする.
また,
の対称式である.以下,和は異なる添え字にわたるものとする.
また,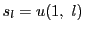 である.
である.
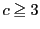 のとき
のとき
また
であるが,
の展開のなかで,異なる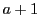 個の積になるものが,そのうちいずれを
個の積になるものが,そのうちいずれを
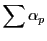 からとるかの場合の数,つまり
からとるかの場合の数,つまり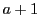 個ずつ現れる.
ゆえに
個ずつ現れる.
ゆえに
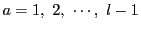 にわたって順次代入することにより
にわたって順次代入することにより
を得る.
□
本補題そのものは,
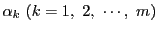 が根である必要はなく,一般の文字で成立する.
が根である必要はなく,一般の文字で成立する.
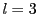 のときは
のときは
という等式である.


 次: 係数定理
上: ζを関・ベルヌーイ数で表す
前: 関・ベルヌーイ数とベルヌーイ多項式
Aozora
2018-05-14
次: 係数定理
上: ζを関・ベルヌーイ数で表す
前: 関・ベルヌーイ数とベルヌーイ多項式
Aozora
2018-05-14
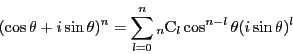
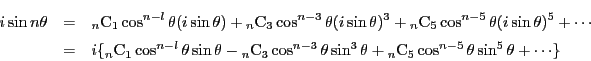
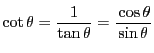 を用いて
を用いて
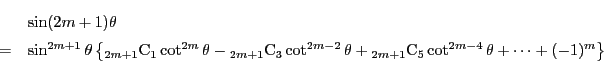
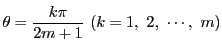 を代入する.
この
を代入する.
この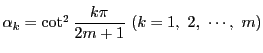 は、
は、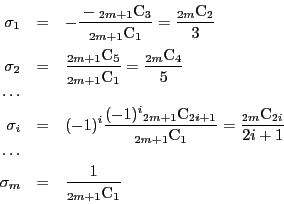
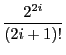 である.
である.
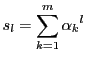 である.
である.
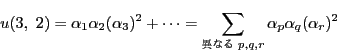
![]() のとき
のとき
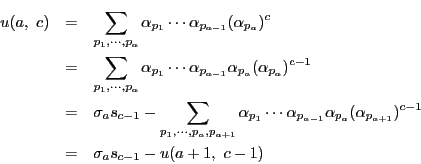
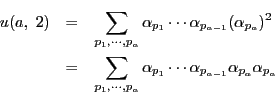
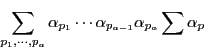
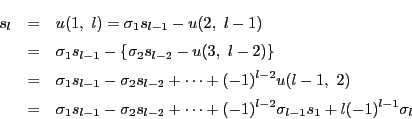
![]() が根である必要はなく,一般の文字で成立する.
が根である必要はなく,一般の文字で成立する.
![]() のときは
のときは