

 次: 定理の一般化
上: ムーアヘッドの不等式とその応用
前: 入試問題の一般化
次: 定理の一般化
上: ムーアヘッドの不等式とその応用
前: 入試問題の一般化
3個の文字の(1, 2, 3)の並び替えは6通り(それ自身を含む)ある.その一つ一つは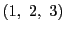 の置きかえであると考えることができる.例えば
の置きかえであると考えることができる.例えば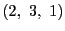 に対しては
に対しては
の置きかえ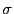 が対応している.一般に
が対応している.一般に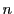 個の文字
個の文字
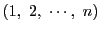 に対して
に対して
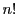 個の置きかえ
個の置きかえ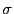 ができる.
ができる.
この記号を用いて表される次の定理をムーアヘッドの定理,その不等式をムーアヘッドの不等式という.
定理 2
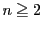
とする.
条件
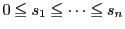 と
と
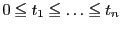 を満たす二つの実数列
を満たす二つの実数列
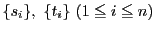 に関する
二つの条件(1)と(2)は,同値である.
に関する
二つの条件(1)と(2)は,同値である.
(1)
| |
|
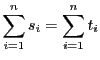 |
(2) |
| |
|
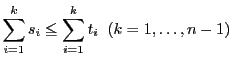 |
(3) |
を満たす.
(2)任意の非負実数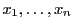 に対し,不等式
に対し,不等式
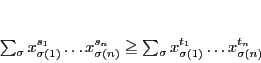 |
(4) |
が成立する.
ここに和は
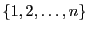
の置きかえ
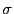
全体にわたる.
同値な条件(1),(2)のもとで,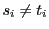 となる
となる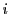 が存在すれば,
等号は
が存在すれば,
等号は
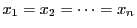 のときのみ成立する.
■
のときのみ成立する.
■
これをムーアヘッドの定理という.
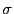 全体にわたる和なので
全体にわたる和なので
でもあることに注意しよう.
例 0.0.1
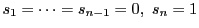
,
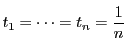
は条件を満たす.
よりこれは相乗平均と相加平均の関係を示す不等式である.
例 0.0.2
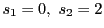
,
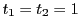
は条件を満たす.
これは次式を意味する.
例 0.0.3
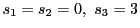
,
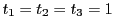
は条件を満たす.
さらに
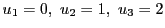
とすると,
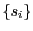
と
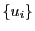
,
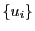
と
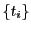
も条件を満たす.
これからムーアヘッドの不等式は次式を意味する.
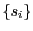 と
と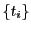 に対して
に対して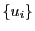 を作りあいだに入れることは,次の定理の証明の中で用いられる.
を作りあいだに入れることは,次の定理の証明の中で用いられる.
以上の例はいずれも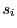 や
や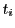 が有理数であるが,これが条件を満たす実数列で成りたつというのが,本定理である.
が有理数であるが,これが条件を満たす実数列で成りたつというのが,本定理である.
(1)ならば(2)が成り立つことを示す.
非負実数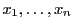 がすべて0なら明らかなので,0でないものがあるとする.
がすべて0なら明らかなので,0でないものがあるとする.
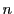 に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
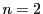 のとき.
のとき.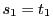 なら
なら
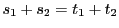 より
より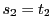 となって等号で成立.
となって等号で成立.
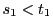 とする.このとき条件から
とする.このとき条件から
である.
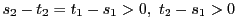 より
より
で等号は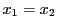 のときにかぎり成立する.よって
のときにかぎり成立する.よって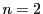 のとき命題は成立する.
のとき命題は成立する.
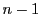 について命題が成立するとする.
について命題が成立するとする.
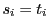 となる
となる があるとき.証明すべき等式は
があるとき.証明すべき等式は
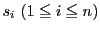 と
と
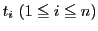 のそれぞれについて対称である.
したがって
のそれぞれについて対称である.
したがって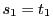 としてよい.このとき.
としてよい.このとき.
ここで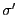 は,和の外にくくったのもが
は,和の外にくくったのもが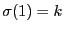 のときは,
のときは,
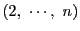 から,1から
から,1から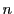 で
で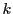 をのぞく
をのぞく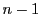 の数への置きかえを意味する.その
の数への置きかえを意味する.その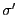 全体の和は,1から
全体の和は,1から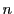 で
で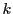 をのぞく
をのぞく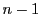 の数から,1から
の数から,1から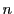 で
で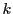 をのぞく
をのぞく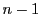 の数への置きかえにわたる和と等しい.
の数への置きかえにわたる和と等しい.
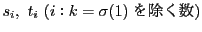 の
の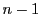 個ずつの数も同じ定理の条件をみたす.
よって数学的帰納法の仮定から
個ずつの数も同じ定理の条件をみたす.
よって数学的帰納法の仮定から
が成り立つ.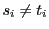 となる
となる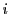 が1から
が1から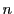 で
で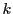 をのぞく
をのぞく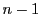 の数の中にあることと
の数の中にあることと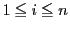 あることが同値であり,非負実数
あることが同値であり,非負実数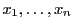 のなかに0でないものがあるので等号成立条件も成り立つ.
のなかに0でないものがあるので等号成立条件も成り立つ.
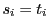 となる
となる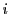 がないとき.
がないとき.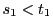 ,
,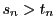 なので,
なので,
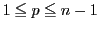 で
で
となる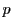 がある.ここで
がある.ここで
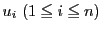 を次のように定義する.
を次のように定義する.
このようにすると
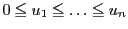 であり,さらに
であり,さらに
が成立する.
ところが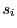 の列と
の列と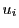 の列,
の列,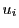 の列と
の列と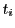 の列にはそれぞれ等しい項がある.
の列にはそれぞれ等しい項がある.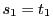 のときの証明と同様にべきの等しい項をくくることで数学的帰納法の仮定から
のときの証明と同様にべきの等しい項をくくることで数学的帰納法の仮定から
となる.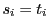 となる
となる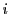 がないことと
がないことと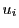 の定義から,べきの等しい項をくくった残余の項の添え数のあいだの和の等号は1文字を除いた他の
の定義から,べきの等しい項をくくった残余の項の添え数のあいだの和の等号は1文字を除いた他の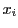 がすべて等しいときにかぎる.この結果,非負実数
がすべて等しいときにかぎる.この結果,非負実数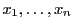 のなかに0でないものがあるので和全体の等号も
のなかに0でないものがあるので和全体の等号も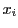 がすべて等しいときにかぎる.つまり,等号成立条件を含めて定理の命題が成立する.かくして
がすべて等しいときにかぎる.つまり,等号成立条件を含めて定理の命題が成立する.かくして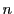 の場合も成立し,(1)ならば(2)が成立することが証明された.
の場合も成立し,(1)ならば(2)が成立することが証明された.
(2)ならば(1)が成り立つことを示す.
(2)の不等式(4)を
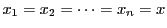 で用いる.この不等式は
で用いる.この不等式は
となる.これが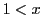 で成立し,かつ
で成立し,かつ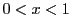 でも成立するので,
でも成立するので,
である.よって等式(2)が成立.
次に,
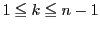 について,
(2)の不等式(4)を
について,
(2)の不等式(4)を
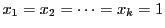 ,
,
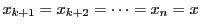 で用いる.この不等式の
両辺の最高次の項はそれぞれ
で用いる.この不等式の
両辺の最高次の項はそれぞれ
となる.
両辺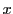 の多項式であるから,
の多項式であるから,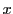 を十分大きくとると,
不等式(4)が成立するために,
を十分大きくとると,
不等式(4)が成立するために,
が必要である.等式(2)とあわせて,
不等式(3)が成立する.
これで(1)の成立が示された.
□
系 1
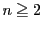
とする.
実数の列
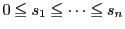
と
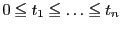
は次の二つの条件,
を満たす.このとき任意の非負実数
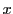
に対し,
不等式
が成立する.
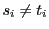
となる
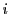
が存在すれば,等号は
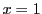
のときのみ成立する.
■
証明
定理2において,
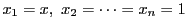 とおく.
和において,
とおく.
和において,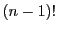 個ずつ同じ項が現れるので,
それを約すると,本不等式になる.
□
個ずつ同じ項が現れるので,
それを約すると,本不等式になる.
□
注意 0.0.1
定理
2の証明を,
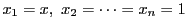
として追ってゆくと,
たいへん簡明な不等式であることがわかる.
適当な総和法を用いて,
数学的帰納法によらず直接に証明が出来そうであるが,
それはまだやっていない.


 次: 定理の一般化
上: ムーアヘッドの不等式とその応用
前: 入試問題の一般化
Aozora
次: 定理の一般化
上: ムーアヘッドの不等式とその応用
前: 入試問題の一般化
Aozora
2013-05-10
![]() と
と
![]() を満たす二つの実数列
を満たす二つの実数列
![]() に関する
二つの条件(1)と(2)は,同値である.
に関する
二つの条件(1)と(2)は,同値である.
![]() に対し,不等式
に対し,不等式
![]() となる
となる![]() が存在すれば,
等号は
が存在すれば,
等号は
![]() のときのみ成立する.
■
のときのみ成立する.
■
![]() 全体にわたる和なので
全体にわたる和なので
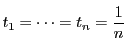 は条件を満たす.
は条件を満たす.
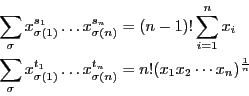
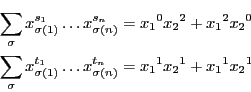
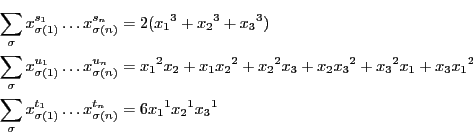
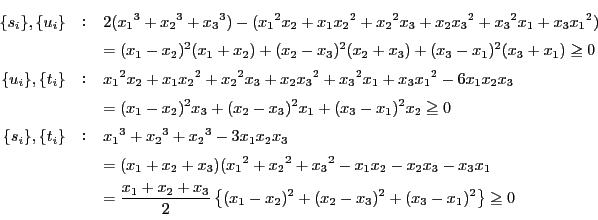
![]() や
や![]() が有理数であるが,これが条件を満たす実数列で成りたつというのが,本定理である.
が有理数であるが,これが条件を満たす実数列で成りたつというのが,本定理である.
![]() がすべて0なら明らかなので,0でないものがあるとする.
がすべて0なら明らかなので,0でないものがあるとする.
![]() に関する数学的帰納法で示す.
に関する数学的帰納法で示す.
![]() のとき.
のとき.![]() なら
なら
![]() より
より![]() となって等号で成立.
となって等号で成立.
![]() とする.このとき条件から
とする.このとき条件から
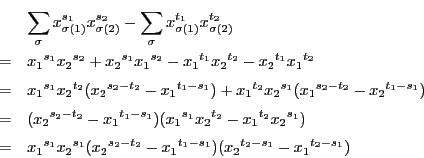
![]() について命題が成立するとする.
について命題が成立するとする.
![]() となる
となる![]() があるとき.証明すべき等式は
があるとき.証明すべき等式は
![]() と
と
![]() のそれぞれについて対称である.
したがって
のそれぞれについて対称である.
したがって![]() としてよい.このとき.
としてよい.このとき.
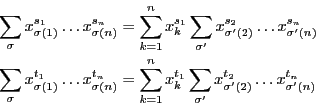
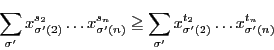
![]() となる
となる![]() がないとき.
がないとき.![]() ,
,![]() なので,
なので,
![]() で
で
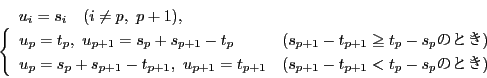
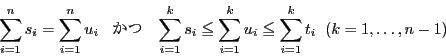
![]() で用いる.この不等式は
で用いる.この不等式は
![]() について,
(2)の不等式(4)を
について,
(2)の不等式(4)を
![]() ,
,
![]() で用いる.この不等式の
両辺の最高次の項はそれぞれ
で用いる.この不等式の
両辺の最高次の項はそれぞれ