
 上: ムーアヘッドの不等式とその応用
前: ムーアヘッドの不等式
上: ムーアヘッドの不等式とその応用
前: ムーアヘッドの不等式
定理1をさらに次のように一般化しよう.
定理 3
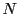
を自然数の定数とし,
数列
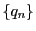
を次式で定義する.
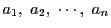
を
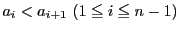
,
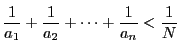
を満たす
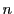
個の自然数とする.不等式
が成立し,等号は
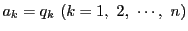
のとき,そしてそのときにかぎる.
■
注意 0.0.2
数列
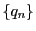
を
N-シルベスター数列といおう.
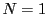 のときが,定理1である.
また本定理の数列
のときが,定理1である.
また本定理の数列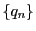 では,
では,
なので,命題
1は定理
3で
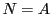
,
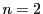
の場合である.
つまり,定理
3は命題
1の一般化でもある.
補題を一つ準備する.
補題 1
定理
3内で定義された数列
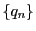
は,関係式
を満たす.
■
証明
数学的帰納法で示す.
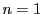 のときは
のときは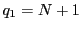 なので,
なので,
より成立.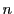 で成立とする.
で成立とする.
つまり,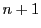 のときも成立する.
よって命題はすべての
のときも成立する.
よって命題はすべての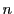 で成立する.
□
で成立する.
□
定理3の成立を,
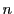 についての数学的帰納法で示す.
についての数学的帰納法で示す.
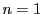 のときは
のときは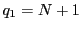 なので
なので
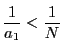 なら
なら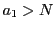 ,つまり
,つまり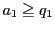 である.よって
である.よって
は成立し,等号成立は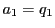 のときにかぎる.
のときにかぎる.
定理3の命題の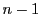 以下での成立を仮定する.
以下での成立を仮定する.
と表すとき,
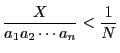 より
より
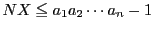 である.
よって
である.
よって
である.
補題1より
なので,
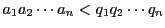 なら
なら
となり成立.
以下では
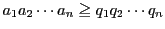 とする.
とする.
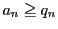 のとき.
帰納法の仮定により成立する
のとき.
帰納法の仮定により成立する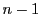 のときの不等式の両辺に,
のときの不等式の両辺に,
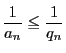 を加えると
を加えると
となり,等号成立条件も成立する.
よって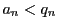 とする.
このとき不等式の成立と等号の不成立を示せばよい.
とする.
このとき不等式の成立と等号の不成立を示せばよい.
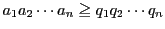 とあわせると,
番号
とあわせると,
番号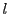 で
で
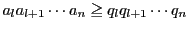 となる最大のものがある.
それを
となる最大のものがある.
それを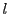 とする.
とする.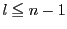 である.
である.
であるから
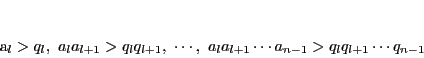 |
(5) |
である.有理数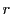 と整数
と整数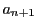 を
を
で定める.
である.ここで
とする.この実数の列は条件
を満たし,さらにその定義と不等式列(5)より
を満たす.(注:「<」を「≦」に訂正.) ただしk=1,…,n-l の範囲では等号不成立.つまり系1の条件を満たす.
で系1を用いる.この場合,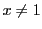 から,等号は成立しない.
から,等号は成立しない.
\begin{eqnarray*}
&&\sum_{i=1}^{n-l+2}e^{-s_i}=\sum_{i=1}^{n-l+1}e^{-\log(q_{l+i-1})}+e^{-\log r}\\
&>&
\sum_{i=1}^{n-l+2}e^{-t_i}=\sum_{i=1}^{n-l+2}e^{-\log(a_{l+i-1})}
\end{eqnarray*}
を得る.これから
を得る.ここで,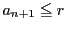 より
より
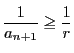 なので,
なので,
である.
帰納法の仮定から
は成立.両辺加えて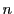 のときの成立が示され,等号成立条件も示されている.
□
のときの成立が示され,等号成立条件も示されている.
□
太郎
ムーアヘッドの不等式といっても,
系1の形で,つまり
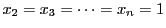 の場合に使うだけですね.
の場合に使うだけですね.
南海
そうなのだ.
ムーアヘッドの不等式の証明を
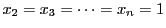 の場合に書き出してみると,
案外簡単な証明だ.先にも言ったが直接の証明もできそうだ.
の場合に書き出してみると,
案外簡単な証明だ.先にも言ったが直接の証明もできそうだ.
ただ,ムーアヘッドの不等式は,たいへん面白いし,
多くの具体的な不等式を生みだす.
置換群の記号が出てくるので,少しとっつきにくいが,ぜひ自分で後を追ってみてほしい.

 上: ムーアヘッドの不等式とその応用
前: ムーアヘッドの不等式
Aozora
上: ムーアヘッドの不等式とその応用
前: ムーアヘッドの不等式
Aozora
2013-05-10
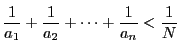 を満たす
を満たす![]() のときは
のときは![]() なので,
なので,
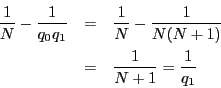
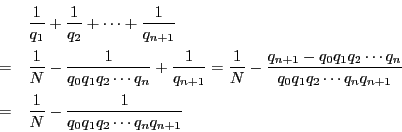
![]() のときは
のときは![]() なので
なので
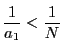 なら
なら![]() ,つまり
,つまり![]() である.よって
である.よって
![]() 以下での成立を仮定する.
以下での成立を仮定する.
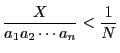 より
より
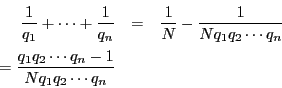
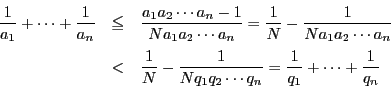
![]() とする.
とする.
![]() のとき.
帰納法の仮定により成立する
のとき.
帰納法の仮定により成立する![]() のときの不等式の両辺に,
のときの不等式の両辺に,
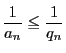 を加えると
を加えると
![]() とする.
このとき不等式の成立と等号の不成立を示せばよい.
とする.
このとき不等式の成立と等号の不成立を示せばよい.
![]() とあわせると,
番号
とあわせると,
番号![]() で
で
![]() となる最大のものがある.
それを
となる最大のものがある.
それを![]() とする.
とする.![]() である.
である.
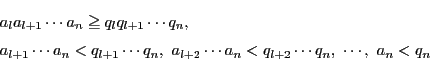
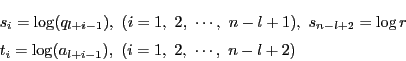
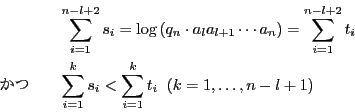
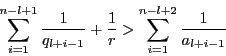
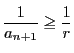 なので,
なので,
![]() の場合に使うだけですね.
の場合に使うだけですね.
![]() の場合に書き出してみると,
案外簡単な証明だ.先にも言ったが直接の証明もできそうだ.
の場合に書き出してみると,
案外簡単な証明だ.先にも言ったが直接の証明もできそうだ.