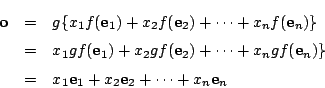次: 基底変換と行列の変換
上: 線型写像と行列
前: 線型写像の演算と行列の演算
南海
写像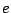 は,任意のベクトル
は,任意のベクトル
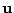 に対して
に対して
が成り立つとき,恒等写像という.
恒等写像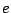 と任意の写像
と任意の写像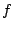 に対して
に対して
が成り立つ.
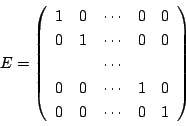
恒等写像を表現する行列は基底のとり方にかかわらず
である.これを単位行列という.
線型写像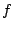 に対して
に対して
が成り立つ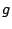 が存在するとき,
が存在するとき,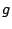 を
を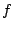 の逆写像という.
この
の逆写像という.
この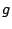 を
を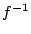 と書きあらわす.
と書きあらわす.
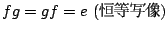 となる
となる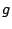 が存在するとき,
が存在するとき,
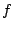 はベクトル空間
はベクトル空間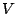 の一対一写像である.
なぜなら
の一対一写像である.
なぜなら
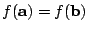 となれば
となれば
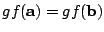 で
で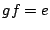 より
より
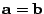 となり,
となり,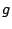 についても同様に示されるからである.
についても同様に示されるからである.
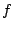 に対応する行列を
に対応する行列を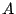 ,
,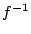 に対応する行列を
に対応する行列を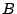 とすると,
とすると,
が成り立つ.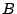 のことを行列
のことを行列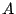 の逆行列という.
の逆行列という.
写像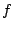 に逆写像が存在するための条件が次のように基底の概念を用いて言い表される.
に逆写像が存在するための条件が次のように基底の概念を用いて言い表される.
定理 3
ベクトル空間
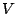
から
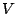
への写像
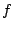
が逆写像
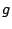
をもつための必要十分条件は,
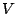
の一組の基底
に対して
もまた
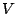
の基底となることである.
証明
が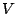 の基底であるとき.基底の定義から,
の基底であるとき.基底の定義から,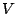 の任意のベクトルは
の任意のベクトルは
と表される.この基底で表されたベクトルを
に移す写像を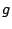 とする.これは明らかに線型写像である.
一方,
とする.これは明らかに線型写像である.
一方,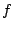 は
は
を
に移す写像である.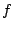 と
と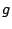 はこの二つのベクトルを相互に移す写像である.
よって
はこの二つのベクトルを相互に移す写像である.
よって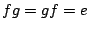 が成り立つ.
が成り立つ.
逆に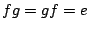 となる
となる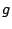 が存在するとする.このとき
が存在するとする.このとき
が一次独立でないとし,関係
が成り立つとする.このとき
これは
が基底であることと矛盾.ゆえに
は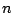 個の一次独立なベクトルである.つまり基底であることが示された.
□
個の一次独立なベクトルである.つまり基底であることが示された.
□
演習 6
解答
6
 座標の定まった平面ベクトル空間で,基底
座標の定まった平面ベクトル空間で,基底
をとる.線型写像
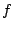
を
で定めるとき,逆写像
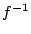
を求めよ.



次: 基底変換と行列の変換
上: 線型写像と行列
前: 線型写像の演算と行列の演算
Aozora Gakuen
![]() に対して
に対して
![]() となる
となる![]() が存在するとき,
が存在するとき,
![]() はベクトル空間
はベクトル空間![]() の一対一写像である.
なぜなら
の一対一写像である.
なぜなら
![]() となれば
となれば
![]() で
で![]() より
より
![]() となり,
となり,![]() についても同様に示されるからである.
についても同様に示されるからである.
![]() に対応する行列を
に対応する行列を![]() ,
,![]() に対応する行列を
に対応する行列を![]() とすると,
とすると,
![]() に逆写像が存在するための条件が次のように基底の概念を用いて言い表される.
に逆写像が存在するための条件が次のように基底の概念を用いて言い表される.
![]() となる
となる![]() が存在するとする.このとき
が存在するとする.このとき