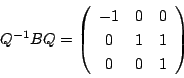-
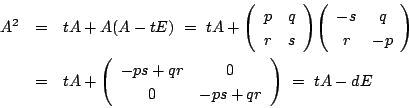
-
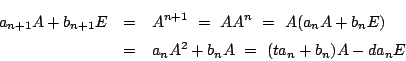
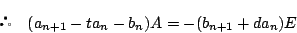
ここで,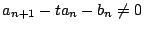 なら,
なら,
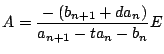 となるので仮定に反する. したがって
となるので仮定に反する. したがって
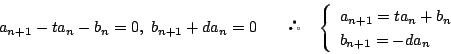
-
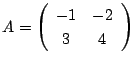 のとき,
のとき, 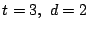 である. つまり
である. つまり
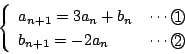
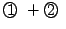 から
から
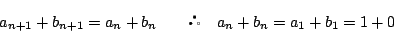
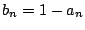 を1に代入する.
を1に代入する.
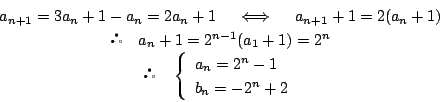
よって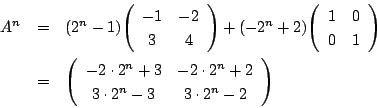
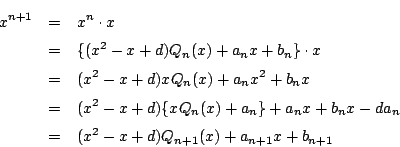
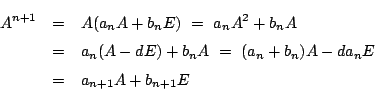
別解1
![]() のときは上と同様.
のときは上と同様.
![]() のとき,
のとき,
![]() . つまり,
. つまり, ![]() でなければならない.一方
でなければならない.一方 ![]() より,
より, ![]() なので成立.
なので成立.
![]() で成立するとする.
で成立するとする.
![]() より,
より,
![]() .よって
.よって
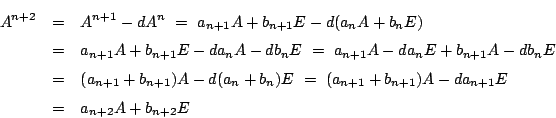
別解2
![]() なので行列
なので行列 ![]() の多項式の積は文字の場合の展開と同様にできる.
の多項式の積は文字の場合の展開と同様にできる.
よって,恒等式 ![]() に対して
に対して ![]() が成り立つ.
が成り立つ.
したがって,
![]() より
より
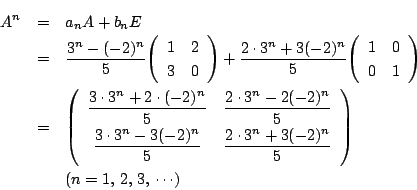
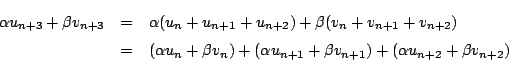
![]() については 数列
については 数列
![]() の条件から成立する.
の条件から成立する.
![]() で成立したとする.
で成立したとする.
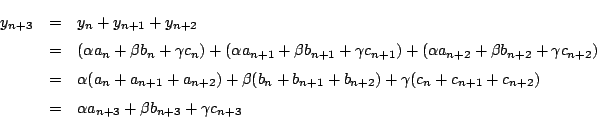
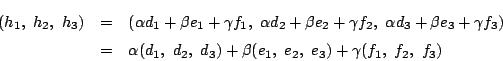
ゆえにどのように
![]() を選んでも 数列
を選んでも 数列 ![]() を
題意のように表すことはできない
を
題意のように表すことはできない
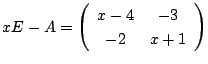 が逆行列をもたないので
が逆行列をもたないので
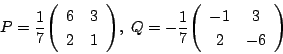
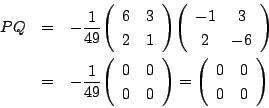
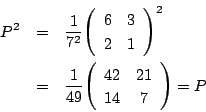
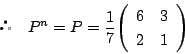
![]() のとき.
のとき.
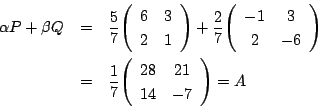
![]() のとき
のとき
![]() とする.(1)と同様に
とする.(1)と同様に![]() でもある.
でもある.
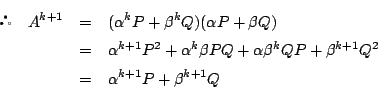
別解
※上の計算では単に計算するだけなので,もう少しなぜこのようになるのかわかるように証明しておく. 冒頭の部分は同じ.
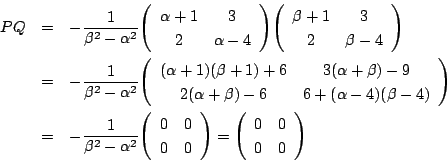
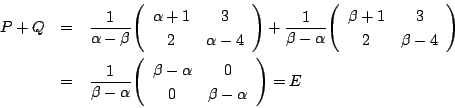
ゆえに本解と同様に![]() である.
である.
ここで
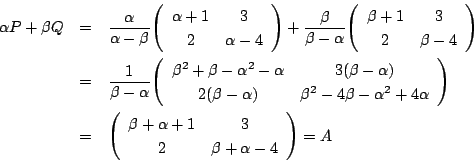
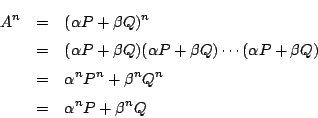

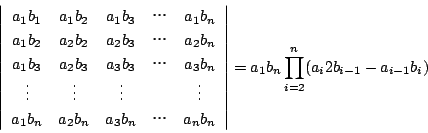
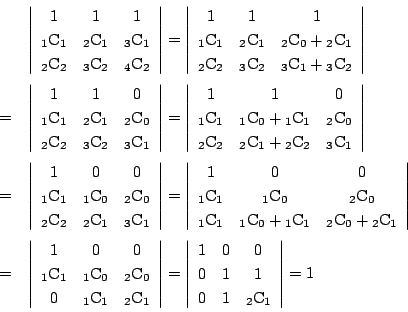
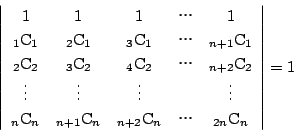
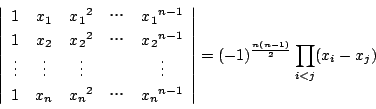
(1)
最小多項式は
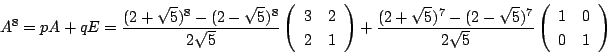
(2)
最小多項式は![]() .
.
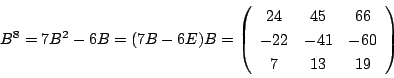
(1)
特性方程式は
![]() のとき,
のとき,
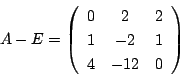
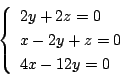
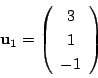
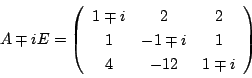
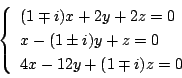
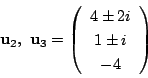
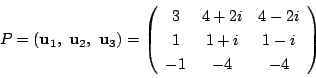
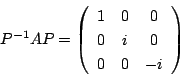
(2) 特性方程式を Asir で因数分解すると
[0] B-tE=newmat(3,3,[[-4-t,9,-4],[-9,18-t,-8],[-15,29,-13-t]]); [ -t-4 9 -4 ][ -9 -t+18 -8 ][ -15 29 -t-13 ] [1] fctr(det(B)); [[-1,1],[t-1,2],[t+1,]]特性方程式は
![]() のとき.
のとき.
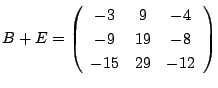 である.
対応する固有ベクトルを次のもにとる.
である.
対応する固有ベクトルを次のもにとる.
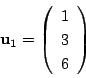
![]() のとき.
のとき.
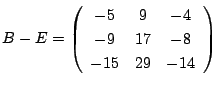 で,また Asir で計算すると,
で,また Asir で計算すると,
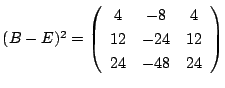 である.これから
である.これから
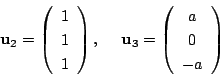
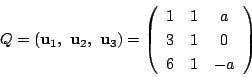
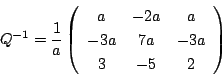
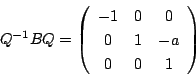
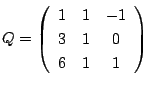 とするとき標準形は次のものになる.
とするとき標準形は次のものになる.