次: 直交変換と直交行列
上: 内積と直交変換
前: 内積の対角型行列表示
ベクトル空間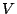 と内積
と内積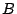 が与えられている.
定理によって,適当な基底をとると,内積が対称行列
が与えられている.
定理によって,適当な基底をとると,内積が対称行列
 で表された.
で表された.
この基底を
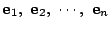 とする.
ベクトル
とする.
ベクトル
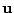 をこの基底で表して
をこの基底で表して
とすると,
となるのであった.
したがってとくに
となる.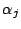 はすべて正なので,
はすべて正なので,
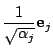 を
改めて基底
を
改めて基底
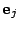 にとると,この基底に関して内積は
にとると,この基底に関して内積は
となる.この基底を内積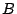 に関する正規直交基底という.
上の〔 〕内に書いたようにそれぞれの性質を正規性,直交性という.
に関する正規直交基底という.
上の〔 〕内に書いたようにそれぞれの性質を正規性,直交性という.
耕一
正規直交基底で
と表されるベクトルの内積は
となります.任意の正値をとる内積から出発して,結局普通の内積になりました.
南海
そういうことなのだ.
ベクトル空間に内積が与えられると,これから
でベクトルの大きさが定義される.
このように大きさが与えられたベクトル空間をユークリッド空間という.
耕一
ベクトルの大きさということは,2点を結ぶベクトルの大きさ,
つまり2点間の距離が定まると言うことですか.
南海
そう.
距離が与えられれば,二次形式から内積を作ったのと同じように内積が定まる.内積を与えることと,距離を与えることとは同値なのだ.
Aozora Gakuen
 で表された.
で表された.
![]() とする.
ベクトル
とする.
ベクトル
![]() をこの基底で表して
をこの基底で表して
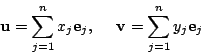
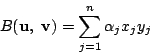
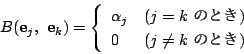
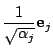 を
改めて基底
を
改めて基底