![]() の1次変換
の1次変換![]() が,任意のベクトルに関してその大きさを変えないとき,
が,任意のベクトルに関してその大きさを変えないとき,
![]() は正規直交変換と呼ばれる.略して直交変換ということも多い.
は正規直交変換と呼ばれる.略して直交変換ということも多い.
耕一
つまり,任意のベクトル
![]() に関して
に関して
![]() をこの基底で行列で表して得られる行列を
をこの基底で行列で表して得られる行列を![]() とします.
また
とします.
また
![]() の成分を
の成分を
![]() とすれば
とすれば
![]() が直交変換であるということは
が直交変換であるということは
南海 これをみたす行列を直交行列とよぼう. これから直ちに直交行列は次のような性質をもつことがわかる.
耕一
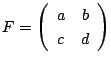 とおくと,
とおくと,
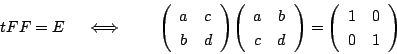
![]() とおくと,
とおくと,![]() から
から
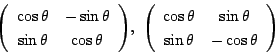
南海
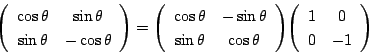
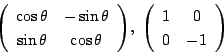
耕一
回転と![]() 軸での対称変換ですね.
軸での対称変換ですね.
南海
以上が線型代数の基本である.概念をつかむことを主にした.
計算問題は多くない.線型代数の参考書はたくさんあるので,
それらによって計算練習をつんでほしい.