次: 解ける根拠 上: 問題を解く 前: 数学の問題

問題の形式

2008年京大の例

数学の問題を形式から見てみよう．実際の入試問題ではどのようになっているのだろうか．京都大学は基本的に1題を小問に分けない形式で出題している．そのためどのような出題であるかを数えるのに適している．2009年はそれぞれ1問ずつ小問に分かれそれを含めて異なる問題が理系甲乙文系あわせて17題が出題された．そのうち「求めよ」が11題，「示せ」が6題である．何を，求めよあるいは示せといっているのか． 実は2008年も，問題総数，配分ともまったく同じであった． ちなみに2008年は次のような内容である．

$$\begin{array}{lll} 問題&種類&内容\\ 理系甲1... ...の個数\\ 文系5&求めよ&場合の数 \end{array}$$

入試問題の中には「図示せよ」などもあるがこれは領域を求めることであるから，基本的にいって入試問題は，なんらかの数学的結果を求めよというものと，示せ，つまり証明せよというものに大別されることがわかる．その過程にヒントを与えるために小問に分かれていることが多いのだが，最後は「求めよ」か「示せ」である．

「求めよ」というのはどういうことか．これはいいかえると「未知なるものを決定せよ」ということである．解を決定せよ，解の個数を決定せよ，体積を決定せよ，そして条件(単に条件といえば必要十分条件のことである)を決定せよ等である．このように入試問題の一つの形は決定問題であるといえる．

「示せ」といわれるもう一つの形はいうまでもなく証明問題である．だがこの二つの形式はその内容においては互いに入り組んでいる．決定問題が証明問題でもあり，証明問題が決定問題でもある．

決定問題は証明問題である

決定問題は結論だけ出せばよいのではなく，それ以外にあり得ないことの論証が必要である．

例題 2.1       ［08一橋］

$k$を正の整数とする．$5n^2-2kn+1<0$を満たす整数$n$が， ちょうど1個であるような$k$をすべて求めよ．

もしこの問題の「すべて求めよ」が単に「求めよ」であったなら，問題は変わるのだろうか．「求めよ」だけなら少なくとも一つ求めればいいのか．そんなことはない．「求めよ」だけであっても条件を満たすものすべてを決定しなければならないし，それですべてであること，その他にはないことの証明がなされていなければならない．だからまず必要条件で範囲を絞り，その範囲の一つ一つを調べて条件を満たすものを決定しなければならない．

未知なるものを求める決定問題は，正しい決定内容ととりうる値がそれだけであることの証明の両方が必要である．そのように解答をつくってみよう．

解答      $5n^2-2kn+1<0$を満たす整数が存在するために， 2次方程式$5x^2-2kx+1=0$が相異なる2実解をもつことが必要である． 判別式を$D$とする．

$$D/4=k^2-5>0$$

$k$が正整数なので$3\le k$．

この2次方程式の二つの解を $\alpha,\ \beta$とする． $\left\vert\beta-\alpha \right\vert>2$なら少なくとも2個存在するので，

$$\left\vert\beta-\alpha \right\vert\le2$$

が必要である．

$$(\beta-\alpha)^2=(\beta+\alpha)^2-4\alpha\beta =\left(\dfrac{2k}{5} \right)^2-\dfrac{4}{5}\le4$$

なので$k^2\le30$となる．2つの条件から$k=3,\ 4,\ 5$が必要である．

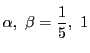$k=3$のとき． $\alpha,\ \beta=\dfrac{1}{5},\ 1$となり，条件を満たす$n$はない．

$k=4$のとき． $\alpha,\ \beta=\dfrac{4\pm\sqrt{11}}{5}$となり，

$$0<\dfrac{4-\sqrt{11}}{5}<1<\dfrac{4+\sqrt{11}}{5}<2$$

であるから，条件を満たす．

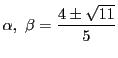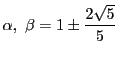$k=5$のとき． $\alpha,\ \beta=1\pm\dfrac{2\sqrt{5}}{5}$となり 同様に条件を満たす．

ゆえに条件を満たすのは$k=4,\ 5$である． □

証明問題は真偽決定問題である

逆に証明問題の内容は真か偽のいずれであるかを決定する問題と見ることができる．

例題 2.2       ［07京大文系］

$n$を1以上の整数とするとき，次の2つの命題はそれぞれ正しいか． 正しいときは証明し，正しくないときはその理由を述べよ．

命題$p$： ある$n$に対して，$\sqrt{n}$と$\sqrt{n+1}$は共に有理数である．
命題$q$： すべての$n$に対して， $\sqrt{n+1}-\sqrt{n}$は無理数である．

これは分類としては論証問題に入るのだろう．が，それぞれ根拠を示して真か偽かを決定せよといっている．つまり問題の形式は真偽の決定である．一般にある命題$A$とその否定$\overline{A}$について

命題$A$およびその否定$\overline{A}$のいずれか一方が真であり他方は偽である． それは確定する．

が成り立つ．命題とその否定のいずれかが成り立ち「いずれでもない」や第三の結論はない．このことを排中律というのだが，現代数学はこの排中律を公理として認めて建設されている．だから背理法が可能なのだ．いずれにしても真か偽以外はない．したがって真であることを示すか，反例をあげて偽であることを示すか，いずれかを行う．

解答      命題$p$は正しくない． それを示す．

$\sqrt{n}$と$\sqrt{n+1}$が共に有理数であるような 自然数$n$が存在したとする．

$$\sqrt{n}=\dfrac{p}{q}\ (p,\ q\ は互いに素な自然数)$$

とおく．これから

$$n=\dfrac{p^2}{q^2}$$

左辺は整数である．ところが $p^2$と$q^2$も互いに素である． これから$q^2=1$．つまり$q=1$となり$\sqrt{n}$は整数$p$である． 同様に$\sqrt{n+1}$も整数である．したがって 二つの自然数$p$と$r$を用いて

$$n=p^2,\ n+1=r^2$$

とおける．ところがこれから$n$を消去すると

$$1=r^2-p^2=(r+p)(r-p)$$

$r$と$p$は自然数なので，$r+p=r-p=1$であるが， このとき$r=1,\ p=0$となり，$n$が自然数であることに反する． よって$\sqrt{n}$と$\sqrt{n+1}$が共に有理数であるような 自然数$n$は存在しない．

命題$q$は正しい． それを示す．

ある$n$で $\sqrt{n+1}-\sqrt{n}$が有理数$\alpha$になったとする． 命題$p$は偽なので， $\sqrt{n+1},\ \sqrt{n}$のいずれもが有理数ということはない． $\sqrt{n}$が無理数のとき$\sqrt{n+1}$が有理数なら $\sqrt{n+1}-\alpha=\sqrt{n}$で左辺有理数なので$\sqrt{n}$が無理数であることに矛盾． 逆のときも同様に矛盾する． したがって $\sqrt{n+1},\ \sqrt{n}$はともに無理数である． $\sqrt{n}=\omega\ (無理数)$とおく． すると $\sqrt{n+1}=\alpha+\omega$となる．$\alpha\ne 0$である． このとき

$$n+1=\alpha^2+2\alpha\omega+\omega^2=\alpha^2+2\alpha\omega+n$$

これから

$$\omega=\dfrac{1-\alpha^2}{2\alpha}$$

左辺は無理数で右辺は有理数なので矛盾である． よって $\sqrt{n+1}-\sqrt{n}$が有理数となる$n$は存在しない． □

命題$q$が正しいことの証明は次のようにすることもできる．
別解     ある$n$で $\sqrt{n+1}-\sqrt{n}$が有理数$\alpha$になったとする． 明らかに$\alpha\ne 0$である．そこで

$$\dfrac{1}{\alpha}=\dfrac{1}{\sqrt{n+1}-\sqrt{n}}=\sqrt{n+1}+\sqrt{n}$$

これから

$$\sqrt{n+1}=\dfrac{1}{2}\left(\alpha+\dfrac{1}{\alpha} \righ... ... \sqrt{n}=\dfrac{1}{2}\left(-\alpha+\dfrac{1}{\alpha} \right)$$

となり， $\sqrt{n+1},\ \sqrt{n}$がともに有理数となる．これは 命題$p$が偽であることと矛盾する． □

多くの証明問題は「真であること(成立すること)を証明せよ」と「真」という結論を先に示し，そのうえで証明だけを問うものになることが多い．しかし本来はこの京大の問題のように，真か偽かわからないところから探求するのが問題である．この意味で，命題を証明する証明問題は，より一般的にいえば，命題が真か偽かのいずれであるかを決定する問題なのである．だからこの意味では証明問題も決定問題なのだ．

いずれにせよ数学の問題は，未知なるものの値を決定しその根拠を明示することを要求する．ここでいう「値」とは，単に数値という意味ではない．最大値や最小値のような値であることが多いのだが，実数の区間であったり，一定の不等式で定まる領域であったり，さらにまた命題の属性としての「真」か「偽」(それを真理値ということもある)であることもある．

問題には謙虚な姿勢で

ところで数学の問題というのは恣意的に作られたものなのだろうか．実はそうではない．どのように簡単な問題でも，数学の問題であるかぎりは数学的現象のある側面を切りとったものなのだ．数学的な現象を体系化してつかむ方法や形式は自由である．しかしつかまれる数学的事実，数学的現象そのものは，客観的に存在している．大きな木も，珍しく貴重な植物も，道端の雑草も同じ植物だ．植物としての神秘をもっている．これと同じように最先端の数学も入試数学も同じ数学なのだ．だから問題に対しては謙虚な姿勢で向かわなければならない．

次: 解ける根拠 上: 問題を解く 前: 数学の問題