

 次: 二論は同等
上: 実数の構成
前: 数列の方法
次: 二論は同等
上: 実数の構成
前: 数列の方法
有理数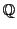 が二つの集合
が二つの集合 と
と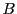 の和集合で,
の和集合で, の任意の要素
の任意の要素 と
と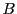 の任意の要素
の任意の要素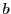 の間につねに
の間につねに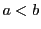 が成り立っているとき,これを
が成り立っているとき,これを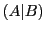 と書いて「切断」と呼ぶ.
と書いて「切断」と呼ぶ. を
を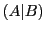 の下組,
の下組,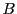 を上組という.
を上組という.
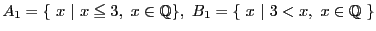 とする.この切断
とする.この切断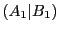 は有理数3を定める.
は有理数3を定める.
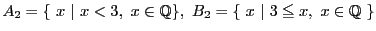 とする.としたときも切断
とする.としたときも切断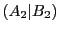 は有理数3を定める.
これは理解できる.
は有理数3を定める.
これは理解できる.
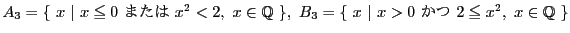 とすると,
とすると,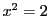 となる有理数は存在しないのだから,この境目になる有理数はない.実数ならいわゆる
となる有理数は存在しないのだから,この境目になる有理数はない.実数ならいわゆる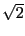 が対応するが,有理数のなかではこの切断の境目となる数は存在しない.しかし逆に見ると,有理数だけを用いて
が対応するが,有理数のなかではこの切断の境目となる数は存在しない.しかし逆に見ると,有理数だけを用いて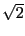 が指示できている.有理数を用いて実数を指示できる.それなら有理数から実数を構成する方法として,切断の集合
が指示できている.有理数を用いて実数を指示できる.それなら有理数から実数を構成する方法として,切断の集合
を考えればよいのではないか. から
から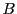 か,
か,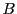 から
から かへ1つの要素を動かしてそれを
かへ1つの要素を動かしてそれを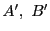 とするとき
とするとき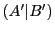 も切断になるなら
も切断になるなら
とする.上の例では
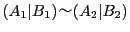 である.
である.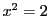 となる有理数はないのだから,
となる有理数はないのだから,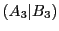 はと同値なものは他にない.
はと同値なものは他にない.
切断の集合の同値関係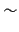 による商集合を
による商集合を
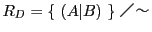 とおく.
とおく.
定理 14
集合
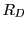
には四則演算,大小関係が定義でき,
実数の公理を満たす.
■
以下方針のみとし証明は一部を除き略する.
まず,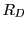 には有理数
には有理数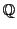 が自然に埋め込まれる.
また,
が自然に埋め込まれる.
また, の順序と整合する自然な順序が定義できる.
の順序と整合する自然な順序が定義できる.
つまり,切断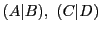 に対して異なる実数が定まるとする.
したがって
に対して異なる実数が定まるとする.
したがって と
と は一方の要素を動かして他方になるということも,
等しいこともない,とする.
は一方の要素を動かして他方になるということも,
等しいこともない,とする.
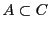 なら
なら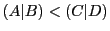 ,
,
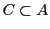 なら
なら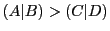 とすればよい.
これによって
とすればよい.
これによって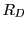 に順序が入る.
に順序が入る.
加法は次のように定めればよい.
 と
と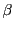 がそれぞれ切断
がそれぞれ切断
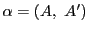 ,
,
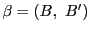 で定義されているとする.
で定義されているとする.
とし,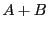 の補集合を
の補集合を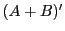 とするとき,
とするとき,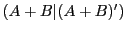 は切断であることが示される.
この切断で定まる
は切断であることが示される.
この切断で定まる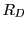 の要素を
の要素を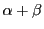 と定める.
これをもとに加法の逆元,0などを構成する.
この加法と順序は順序の公理を満たす.
と定める.
これをもとに加法の逆元,0などを構成する.
この加法と順序は順序の公理を満たす.
ここでは積を定義し,それが定義になっていることを示そう.
以下の定義は青空学園数学科の『解析概論』読書会における Kanneyさんの定義であり,
証明は南海によるものである.
定義 12 (切断の集合での積の定義)

の切断で0を含まない組を
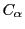
,
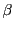
のそれを
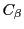
とし,
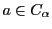
,
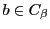
の積
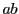
の集合を
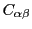
とする.
それはある切断の0を含まないほうの組である.この切断をもって積
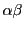
を定義する.
■
これで積が定義できていることを示す.
切断が有理数のときは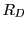 と
と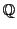 の切断を同一視し,
具体的に考えるときは境界は上の集合に入れることにする.
の切断を同一視し,
具体的に考えるときは境界は上の集合に入れることにする.
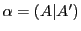 ,
,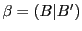 とする.
以下集合はすべて
とする.
以下集合はすべて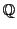 の部分集合である.
の部分集合である.
- 1)
-
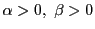 のとき.
のとき.
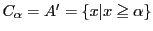 ,
,
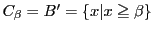 .
(順序は定義できているので有理数と無理数でも不等式は意味がある).
.
(順序は定義できているので有理数と無理数でも不等式は意味がある).
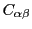 に対し,
に対し,
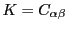 とおく.
とおく.
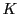 の補集合を
の補集合を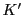 とする.
とする.
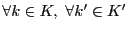 に対し
に対し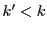 を示せばよい.
を示せばよい.
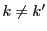 なので,
なので,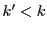 を否定して
を否定して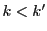 となったとする.
となったとする.
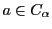 ,
,
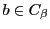 として
として 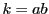 とする.
とする.
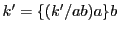 において,
において,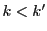 より
より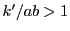 .
よって
.
よって
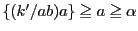 となる.
つまり
となる.
つまり
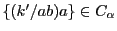 .
.
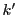 が
が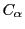 と
と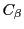 の要素の積で表せたので,
の要素の積で表せたので,
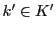 と矛盾.よって
と矛盾.よって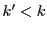 .つまり
.つまり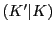 は切断である.
は切断である.
- 2)
-
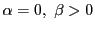 のとき.
のとき.
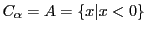 ,
,
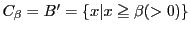 .
そこで
.
そこで
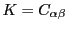 とおく.
とおく.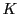 の補集合を
の補集合を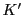 とする.
とする.
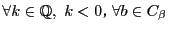 に対して
に対して
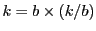 とすれば
とすれば
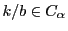 .
よって
.
よって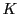 はすべての負の有理数を含む.
明らかに0と正の有理数は含まない.
よって
はすべての負の有理数を含む.
明らかに0と正の有理数は含まない.
よって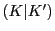 は切断であり0に一致する.
は切断であり0に一致する.
- 3)
-
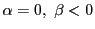 のとき.
のとき.
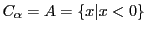 ,
,
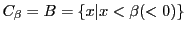 .
そこで
.
そこで
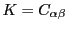 とおく.
とおく.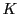 の補集合を
の補集合を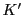 とする.
とする.
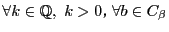 に対して
に対して
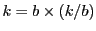 とすれば
とすれば
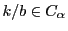 .
よって
.
よって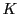 はすべての正の有理数を含む.
明らかに0と負の有理数は含まない.
よって
はすべての正の有理数を含む.
明らかに0と負の有理数は含まない.
よって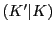 は切断であり0に一致する.
(こうして構成されたものは0が下に含まれる切断になる.
これと0のみを上に移した切断は同じものである).
は切断であり0に一致する.
(こうして構成されたものは0が下に含まれる切断になる.
これと0のみを上に移した切断は同じものである).
- 4)
-
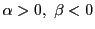 のとき.
のとき.
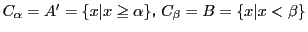 .
.
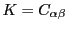 とおく.
とおく.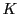 の補集合を
の補集合を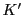 とする.
とする.
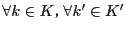 に対し
に対し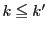 を示せばよい.
を示せばよい.
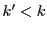 となったとする.
となったとする.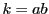 とおく.
とおく.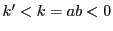 である.
である.
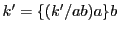 とすると
とすると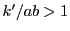 より
より
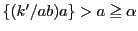 .
よって
.
よって
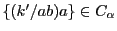 .
したがって
.
したがって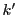 が
が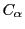 と
と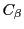 の要素の積で表せたので,
の要素の積で表せたので,
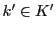 と矛盾.よって
と矛盾.よって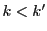 .つまり
.つまり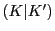 は切断である.
は切断である.
- 5)
-
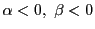 のとき.
のとき.
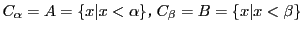 .
.
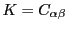 とおく.
とおく.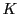 の補集合を
の補集合を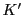 とする.
とする.
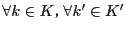 に対し
に対し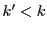 を示せばよい.
を示せばよい.
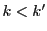 となったとする.
となったとする.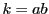 とおく.
とおく.
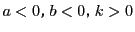 である.
である.
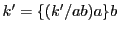 とすると
とすると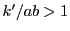 より
より
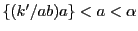 .
よって
.
よって
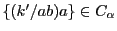 .
したがって
.
したがって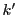 が
が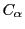 と
と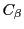 の要素の積で表せたので,
の要素の積で表せたので,
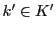 と矛盾.よって
と矛盾.よって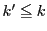 .つまり
.つまり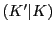 は切断である.
は切断である.
よって積が定義された.
□
この積に関して結合法則が成り立ち,和との間で分配法則が成り立つ.
定理 15
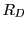
は連続のを満たす.
つまり

を
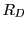
の空でない部分集合とする.
集合

が上に有界ならば

の上限
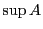
が存在する.
■
証明
 は上に有界なので
は上に有界なので
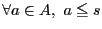 となる
となる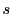 が存在する.
が存在する.
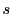 を定める切断を
を定める切断を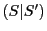 とする.
とする.
である.集合 に属する切断
に属する切断
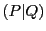 の下組の和集合
の下組の和集合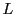 をとる.
をとる.
とおく.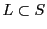 であり,
であり,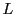 の補集合を
の補集合を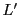 とすると
とすると
となる.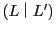 は切断である.この切断の定める実数を
は切断である.この切断の定める実数を とする.
とする.
なので, は
は の上界である.
一方,
の上界である.
一方,
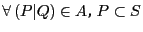 より
より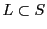 .つまり
.つまり
となる.つまり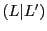 は
は の上界の最小値である.
の上界の最小値である.
□
このようにして,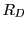 も実数の公理をすべて満たすことが示された.
も実数の公理をすべて満たすことが示された.
定理 16
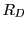
の順序で
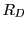
自身に切断が定義される.
この切断も同様に
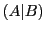
のように表す.
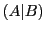
が
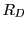
の切断であるとは
このとき,
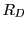
の切断では,

に最大値が存在するか
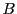
に最小値が存在するか,
いずれかが成り立つ.
■
証明
 は上に有界であるから上限
は上に有界であるから上限 が存在する.
が存在する. が
が に属せば
に属せば の最大値であり,
の最大値であり,
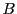 に属せば
に属せば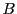 の最小値である.□
の最小値である.□
このようにして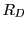 もまた実数の公理をすべて満たすことが示された.
もまた実数の公理をすべて満たすことが示された.


 次: 二論は同等
上: 実数の構成
前: 数列の方法
次: 二論は同等
上: 実数の構成
前: 数列の方法
2014-05-23
![]() とする.この切断
とする.この切断![]() は有理数3を定める.
は有理数3を定める.
![]() とする.としたときも切断
とする.としたときも切断![]() は有理数3を定める.
これは理解できる.
は有理数3を定める.
これは理解できる.
![]() とすると,
とすると,![]() となる有理数は存在しないのだから,この境目になる有理数はない.実数ならいわゆる
となる有理数は存在しないのだから,この境目になる有理数はない.実数ならいわゆる![]() が対応するが,有理数のなかではこの切断の境目となる数は存在しない.しかし逆に見ると,有理数だけを用いて
が対応するが,有理数のなかではこの切断の境目となる数は存在しない.しかし逆に見ると,有理数だけを用いて![]() が指示できている.有理数を用いて実数を指示できる.それなら有理数から実数を構成する方法として,切断の集合
が指示できている.有理数を用いて実数を指示できる.それなら有理数から実数を構成する方法として,切断の集合
![]() による商集合を
による商集合を
![]() とおく.
とおく.
![]() には有理数
には有理数![]() が自然に埋め込まれる.
また,
が自然に埋め込まれる.
また,![]() の順序と整合する自然な順序が定義できる.
の順序と整合する自然な順序が定義できる.
![]() に対して異なる実数が定まるとする.
したがって
に対して異なる実数が定まるとする.
したがって![]() と
と![]() は一方の要素を動かして他方になるということも,
等しいこともない,とする.
は一方の要素を動かして他方になるということも,
等しいこともない,とする.
![]() なら
なら![]() ,
,
![]() なら
なら![]() とすればよい.
これによって
とすればよい.
これによって![]() に順序が入る.
に順序が入る.
![]() と
と![]() がそれぞれ切断
がそれぞれ切断
![]() ,
,
![]() で定義されているとする.
で定義されているとする.
![]() と
と![]() の切断を同一視し,
具体的に考えるときは境界は上の集合に入れることにする.
の切断を同一視し,
具体的に考えるときは境界は上の集合に入れることにする.
![]() ,
,![]() とする.
以下集合はすべて
とする.
以下集合はすべて![]() の部分集合である.
の部分集合である.
![]() なので,
なので,![]() を否定して
を否定して![]() となったとする.
となったとする.
![]() ,
,
![]() として
として ![]() とする.
とする.
![]() において,
において,![]() より
より![]() .
よって
.
よって
![]() となる.
つまり
となる.
つまり
![]() .
.
![]() が
が![]() と
と![]() の要素の積で表せたので,
の要素の積で表せたので,
![]() と矛盾.よって
と矛盾.よって![]() .つまり
.つまり![]() は切断である.
は切断である.
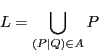
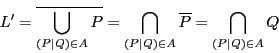
![]() も実数の公理をすべて満たすことが示された.
も実数の公理をすべて満たすことが示された.
![]() もまた実数の公理をすべて満たすことが示された.
もまた実数の公理をすべて満たすことが示された.