 は条件
は条件
が成り立つ.このとき数列
 は収束する.
■
は収束する.
■
カントールによって基本数列を用いる構成では,数の大小関係(順序)を一切使わず,二つの数の間の距離のみを用いている.つまり距離による完備化である.逆に順序は改めて定義しなければならなかった.そのうえで埋め込まれた有理数体の大小関係を用いてアルキメデスの原則が成り立つことを示し,それを用いて上限の存在を示した.
これに対して,デデキントの切断は,二つの有理数の間の距離(長さ)のような概念を一切使わず,ただ数の大小関係(順序)しか使わない.順序を用いた有理数の完備化である.したがってただちに上限の存在は示せた.つまりアルキメデスの原則は定義からの帰結である.
二つの理論は同等である.それを証明するために数列に関するいくつかの定理を示そう.
証明 実数の集合
 は単調増加なので
は単調増加なので
 は,
は,
 は収束する.
■
は収束する.
■
定理と系を一言でいえば,「単調有界数列は収束する」ということである.
 は
は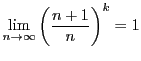 なので
なので
 は
は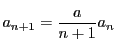 なので
なので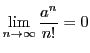 である.
である.
証明 条件(i)から数列
 は単調増加で数列
は単調増加で数列 は上に有界である.
したがって定理17から収束する.
は上に有界である.
したがって定理17から収束する.
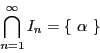
 が有界なので
が有界なので
区間
![]() に属する
に属する![]() が無数にあるとする.
この区間の中点を
が無数にあるとする.
この区間の中点を![]() とする.
2つの区間
とする.
2つの区間![]() ,
,![]() のいずれかには無数の
のいずれかには無数の![]() が属する.
つまり2つの集合
が属する.
つまり2つの集合
数列 の部分列
の部分列
![]() で
で
![]() に収束するものを次のように定める.
に収束するものを次のように定める.

 の部分列であり
の部分列であり
この定理にも歴史がある.
区間を順次二等分することで,区間縮小法を適用した.
この論法はワイエルシュトラスの逐次二等分法といわれている.
数列 の部分列の極限値を数列
の部分列の極限値を数列 の集積値という.
ボルツァノ―ワイエルストラスの定理は集積値という概念を用いると次のようにいえる.
の集積値という.
ボルツァノ―ワイエルストラスの定理は集積値という概念を用いると次のようにいえる.
有界数列には集積値が存在する.
 が上に有界で
単調増加なら
が上に有界で
単調増加なら
![]() がアルキメデスの原則を満たさないとする.
それは任意の自然数
がアルキメデスの原則を満たさないとする.
それは任意の自然数![]() に対して,
に対して,![]() となる正の実数
となる正の実数![]() と
と![]() が存在することを意味する.
である.いいかえると
が存在することを意味する.
である.いいかえると
区間に関する条件から数列 は単調増加,数列
は単調増加,数列![]() は単調減少である.
すべて区間
は単調減少である.
すべて区間![]() に含まれるので有界.3.によりそれぞれ収束する.
極限値を
に含まれるので有界.3.によりそれぞれ収束する.
極限値を![]() ,
,![]() とすると
とすると
こうして,有理数の切断による実数の理論と基本列によるそれとは同等である.同等であるとはつぎの四つの命題が成り立つことを意味する:
この記述は『数学原論』[25]によっている.このようにして定義される順序体は実数体と呼ばれ,これを![]() と書くのであった.
と書くのであった.
最後に,『数の概念』における実数体の定義を述べよう.ここにいたる著者高木貞治の思索の跡については『数とは何か そしてまた何であったか』[23]などを参照されたい.
連続体とはまた,実直線に他ならない.人間は長い歴史を経て,直線というものをこのようにつかんだといえる.
どのような公理を立てるのかがなぜそんなに問題になるのか.それは公理相互の関係を解明し,可能なかぎり一般的で前提の少ない公理系をうち立て,公理相互の関係を研究すること自体が,実数というものの本質を研究することである.
数学的現象は事実として存在する.それを公理系で捉えようとする.公理は絶対的真理ではなく,数学的な対象を捉えるための方法であり,公理相互の関係の中にその対象の本質的が顕れている.