

 次: 不動点定理
上: 次元の拡大
前: 次元の拡大
次: 不動点定理
上: 次元の拡大
前: 次元の拡大
ニュートンにあっては,引力の発見にみられるように,何より自然現象の深い洞察が土台である.万有引力の法則のような定性的な性質の発見は,ただちに位置,速度,加速度のような定量的な洞察を導く.自然の洞察が数学的飛躍を促し、それによって得られた数学的方法による自然の解析がニュートンによって遂行された.こうして、近代になって数学が爆発的に豊かになった.ニュートンの方法を今に再構成したい.
そのためには解析学の方法をもう少し拡げておかねばならない.これまで考えてきた関数の変数は一つであり,値域もまた実数一次元であった.しかしこの世界を見ればわかるように,平面上の位置によって定まる高さのように変数が二つということもあれば,時間という一つの変数に対し三次元空間の位置が定まるということもある.
このようにいくつかの変数の組を扱うためには,これまでの実数から飛躍して,実数 の
の 個の直積である
個の直積である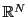 を考えなければならない.
を考えなければならない.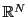 は加法や実数倍の演算が定義されベクトル空間となるが,さらに,ここに距離を入れ
は加法や実数倍の演算が定義されベクトル空間となるが,さらに,ここに距離を入れ 次元ユークリッド空間として
次元ユークリッド空間として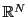 を考えなければならない.距離というもの,およびそれと一体である内積の一般的な定義については『線型代数の考え方』を見てほしい.ここでは実数
を考えなければならない.距離というもの,およびそれと一体である内積の一般的な定義については『線型代数の考え方』を見てほしい.ここでは実数 個の直積
個の直積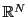 である
である 次元ベクトル空間に距離を次のように定義する.
次元ベクトル空間に距離を次のように定義する.
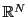 の二つの要素
の二つの要素
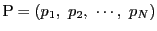 と
と
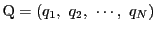 に対し,距離
に対し,距離
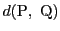 を
を
で定める.距離の定義されたベクトル空間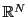 を
を 次元ユークリッド空間という.
次元ユークリッド空間という.
 次元ユークリッド空間
次元ユークリッド空間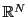 の要素を点という.
実数体
の要素を点という.
実数体 の要素が数直線上の点と同一視できるように,
の要素が数直線上の点と同一視できるように,
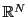 の要素は空間の点やさらに
の要素は空間の点やさらに 次元ベクトルと同一視できる.
次元ベクトルと同一視できる.
ベクトルの概念は元来,現象空間に現れる(速度,加速度,力のように)大きさ,方向,向きを持ち,有向線分によって表される量として導入された.これはまたいくつかの数の組としてもつかむことができた.数一つで表される量をスカラー量といい,複数の数の組で表される量をベクトル量という.
点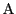 に対し,正の実数
に対し,正の実数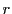 を用いて条件
を用いて条件
を満たす点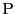 の集合を超球という.
の集合を超球という.
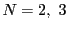 のときは,それぞれ円,球という.
のときは,それぞれ円,球という.
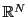 の点の集合
の点の集合 が有界であるとは,
が有界であるとは,
 のすべての要素を含む超球が存在することとする.
のすべての要素を含む超球が存在することとする.
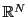 の部分集合
の部分集合 から
から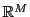 への写像
への写像 を関数という.
を関数という.
 は具体的には
は具体的には
のように表され,各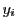 が
が
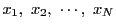 の関数となる.
簡単のために,
の関数となる.
簡単のために,
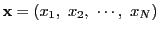 ,
,
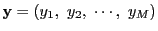 とベクトルの変数を用いて
とベクトルの変数を用いて
とも表す.
このような関数の解析をベクトル解析という.これは三次元ユークリッド空間 内の曲がった管や滑らかな物体
内の曲がった管や滑らかな物体 における流体や電磁場を微積分学を用いて解析する数学手法のことである.ベクトル解析は電磁場の理論を明確に述べるために開発され,物理学や工学等への応用が多い.ここでは後に必要なことにかぎって,その基本部分を構成しておきたい.
における流体や電磁場を微積分学を用いて解析する数学手法のことである.ベクトル解析は電磁場の理論を明確に述べるために開発され,物理学や工学等への応用が多い.ここでは後に必要なことにかぎって,その基本部分を構成しておきたい.
まず問題はこのような関数の連続性である.それを定義するためには,これまで実数の定義にもとづいて構成し証明してきた諸定義と諸定理を, 次元の場合に拡張しなければならない.しかしそれは,
次元の場合に拡張しなければならない.しかしそれは, の場合に絶対値をもとに行ってきた諸々のことを,距離
の場合に絶対値をもとに行ってきた諸々のことを,距離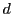 に置きかえて遂行すればよい.
に置きかえて遂行すればよい.
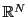 の点列
の点列
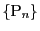 が点
が点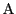 に収束するとは,
任意の正数
に収束するとは,
任意の正数 に対して
に対して
となる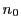 が存在することとし,これを
が存在することとし,これを
と書く.
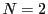 のとき成分で表し
のとき成分で表し
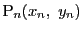 ,
,
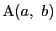 とすると,
とすると,
である.三角不等式から
であるから
である.一般の次元でも同様である.この同値性から,点列の収束に関する諸性質が,
実数列の収束に関する定理から導かれる.
定理 67 (基本列)
点列
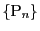
がある.その座標を
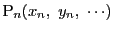
とする.
点列が収束するための必要十分条件は,
点列のそれぞれの座標成分で定まる

個の数列
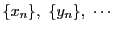
が
ともに基本数列であることである.
■
証明
点列の収束と,全成分の収束の同値性から明らか.
□
 の点の集合
の点の集合 が閉集合であるとは,
が閉集合であるとは,
が成り立つこととする.
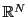 の点集合
の点集合 が開集合であるとは,
が開集合であるとは,
が成り立つこととする.
開集合 に対して,
に対して, を含むすべての閉集合の交わりを
を含むすべての閉集合の交わりを の閉包といい
の閉包といい
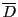 と表す.
と表す.
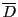 は
は を含む最小の閉集合である.
を含む最小の閉集合である.
本書で領域といえば,開集合のことをいうものとする.
以下は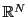 の部分集合
の部分集合 から
から への写像,つまり
実数値関数
への写像,つまり
実数値関数 を考える.
その定義域は
を考える.
その定義域は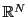 の点集合
の点集合 とする.
とする.
 が点
が点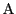 で連続であるとは,任意の正数
で連続であるとは,任意の正数 に対して,
正数
に対して,
正数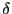 で,
で,
となるものが存在することである.
 が
が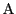 で連続であることは次の条件とも同値である.
で連続であることは次の条件とも同値である.
 内の
内の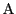 に収束する任意の点列
に収束する任意の点列
 に対して
に対して
が成り立つ.
注意 6.1
次元が2以上になると,
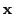
が
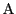
に近づくといっても近づき方は,
はるかに複雑になる.したがって連続性の定義は,「どのような近づき方をしても」関数値が一定の値に近づくということを要請している.
例えば,2変数関数
を考える.
 を
を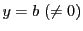 に固定しこの方向から原点に近づくと
に固定しこの方向から原点に近づくと
である.しかし
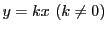
の方向から原点に近づくと
と定数になる.
また渦巻き状に近づくとどうなるか.
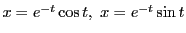
とおいて見る.
となり,収束しない.
このように は原点では連続でない.
変数が多くなると連続性でもこのように複雑になる.
は原点では連続でない.
変数が多くなると連続性でもこのように複雑になる.
定理 68 (最大値・最小値の定理)
実数値をとる関数

が

で連続で

が有界閉集合であるとする.
このとき

は

で最大値,最小値をとる.
■
証明
 が
が で有界でないとする.
で有界でないとする.
 の点列
の点列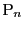 で
で
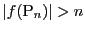 となるものが存在する.
となるものが存在する.
一方, が有界閉集合なので
が有界閉集合なので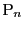 の部分列
の部分列
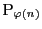 で
で
 の点
の点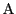 に収束するものが存在する.
に収束するものが存在する. が連続であるから
が連続であるから
と有限確定値に収束する.他方
であるから,矛盾である.よって は
は で有界であり,
で有界であり,
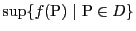 が存在する.この値を
が存在する.この値を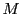 とする.
上限の定義から集合
とする.
上限の定義から集合
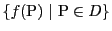 の要素を項とする数列
の要素を項とする数列
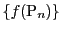 で
で
となるものが存在する.
数列
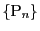 に対し,
ボルツァノ−ワイエルストラスの定理から収束部分列
に対し,
ボルツァノ−ワイエルストラスの定理から収束部分列
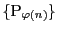 が存在する.
この極限値を
が存在する.
この極限値を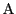 とする.
とする.
 が閉集合なので
が閉集合なので
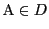 である.
である. が連続なので
が連続なので
となり, は
は で最大値
で最大値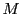 をもつ.
最小値についても同様である.
□
をもつ.
最小値についても同様である.
□
多変数の場合中間値の定理はどのようになるのだろうか.
一変数の場合の中間値の定理では区間![$I=[a,\ b]$](images/img1290.gif) で考えた.
複雑な閉区間は考えていない.
二変数となると定義領域
で考えた.
複雑な閉区間は考えていない.
二変数となると定義領域 についての考察がさらに難しくなる.
次のような形の定理は,一変数の場合から明らかであるが,
についての考察がさらに難しくなる.
次のような形の定理は,一変数の場合から明らかであるが,
 が複雑な場合は難しい.
が複雑な場合は難しい.
 変数でもまったく同様なので二変数の場合に述べる.
変数でもまったく同様なので二変数の場合に述べる.
証明
連続曲線 を,
区間
を,
区間![$[a,\ b]$](images/img797.gif) で定義された連続関数を用いて
で定義された連続関数を用いて
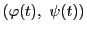 と成分で表す.
と成分で表す.
とする.本定理は一変数の連続関数
に関する中間値の定理(定理26)そのものである.
□
多次元空間の概念をさらに抽象し,
一般の距離空間と完備距離空間の概念を確立する.
定義 29 (距離の公理)
集合

の上に 二変数実数値の写像
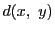
が定義されていて、

の任意の要素
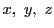
に対して,
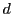
が
距離の公理とよばれる次の性質を全て満たすとする.
- (i)
- 非負性(半正定値性):
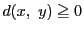 ,
,
- (ii)
- 同一性(非退化性):
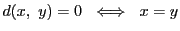 ,
,
- (iii)
- 対称性:
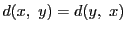 ,
,
- (iv)
- 三角不等式:
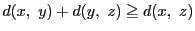
このとき
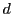
を集合

上の
距離あるいは
距離関数といい,
対
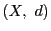
または
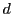
を区別しなくてよいときは単に

を
距離空間という.
■
距離空間の要素のことを点ということもある.
 の点列
の点列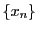 が点
が点 に収束するとは,
任意の正数
に収束するとは,
任意の正数 に対して,
に対して,
となる自然数 が存在することとする.
が存在することとする.
例 6.1
実数体
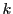
個の直積である
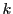
次元空間
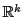
は次のように距離関数を定めるとき
距離空間となる.
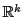
の二つの要素
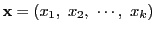
,
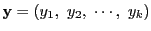
とする.
- (1)
-
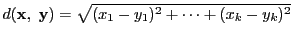
- (2)
-
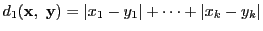
- (3)
-
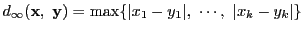
これらがいずれも距離の公理を満たすことを確認しておいてほしい.
不等式
が成立するので,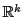 における点列の収束はどの距離をとっても同じことになり,
における点列の収束はどの距離をとっても同じことになり,
 個の座標ごとの収束と一致する.
個の座標ごとの収束と一致する.
定義 30 (基本列)
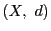
を距離空間とし,

の点列
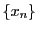
は,
任意の正数

に対して,
となる自然数

が存在するとき,
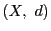
の
基本列,または
コーシー列という.
■
定義 31 (完備距離空間)
距離空間
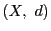
は,そのすべての基本列が

の点に収束するとき
完備
であるといい,
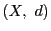
を
完備距離空間であるという.
■
定義 32 (連続写像)
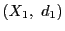
と
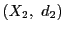
を距離空間とする.
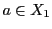
に対して
写像
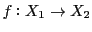
が次の条件:
を満たすとき,

は

で
連続であるという.
任意の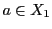 で連続なとき,
で連続なとき, は
は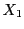 で連続であるという.
■
で連続であるという.
■
連続関数に関する定理25がそのまま距離空間の関数の連続性でも成り立つ.
 が
が で連続であれば
で連続であれば
 に収束する
に収束する の点列
の点列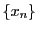 に対し
に対し
が成り立つ. の連続性から,任意の正数
の連続性から,任意の正数 に対して,
に対して,
となる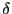 が存在する.この
が存在する.この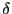 に対し
に対し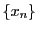 が
が に収束することから
に収束することから
となる が存在する.この
が存在する.この に対して
に対して
なので,所期の等式が得られる.
逆に,
 に収束する
に収束する の点列
の点列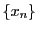 に対し
に対し
が成り立つなら, は連続である.
この証明も,連続関数に関する定理25の証明と同様になされる.
は連続である.
この証明も,連続関数に関する定理25の証明と同様になされる.
距離空間においても点列の収束性が定義されるので,
 の閉集合,開集合も定義される.
つまり
の閉集合,開集合も定義される.
つまり
 の点の集合
の点の集合 が閉集合であるとは,
が閉集合であるとは,
が成り立つこととする.
 の点集合
の点集合 が開集合であるとは,
が開集合であるとは,
が成り立つこととする.
開集合 に対して,
に対して, を含むすべての閉集合の交わりを
を含むすべての閉集合の交わりを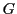 の閉包といい
の閉包といい
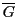 と表す.
と表す.
この証明は定義にもとずいて論理を展開するだけなので省略する.
完備距離空間の一例として連続関数空間を取りあげる.
これが完備であること,この根拠が第1章で展開した実数の完備性であることを確認しよう.
閉区間![$I=[a,\ b]$](images/img1290.gif) で定義された連続関数の集合を
で定義された連続関数の集合を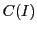 とする.
とする.
 の変数を
の変数を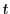 で表す.
で表す.
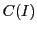 の要素は関数であるがこれを
の要素は関数であるがこれを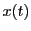 のように表す.
のように表す.
である.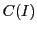 は次のような構造をもっている.
は次のような構造をもっている.
- 1.
- 定値関数は
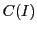 に属する.
実数
に属する.
実数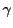 を
を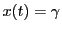 という定値関数と
同一視すれば
という定値関数と
同一視すれば
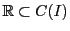 である.
である.
- 2.
-
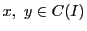 ,
,
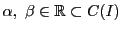 とする.このとき,
とする.このとき,
つまり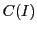 は
は 上の可換環である.
上の可換環である.
- 3.
-
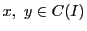 に対し,
に対し,
これらは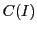 に属する.
に属する.
- 4.
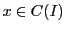 のとき
のとき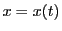 は
は で一様連続であり(定理28),
で一様連続であり(定理28),
 で最大値,最小値ををとる(定理27).
で最大値,最小値ををとる(定理27).
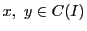 に対し
に対し
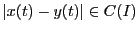 であり,
区間
であり,
区間 における最大値が存在する.
そこで,
における最大値が存在する.
そこで,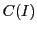 に実数値関数
に実数値関数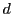 を次のように定義する.
を次のように定義する.
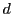 は
は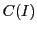 における距離関数である.実際
における距離関数である.実際
- (i)
-
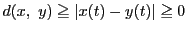 ,
,
- (ii)
- もし
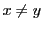 なら
なら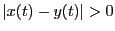 となる
となる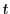 が存在する.
が存在する.
よって
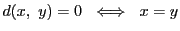 ,
,
- (iii)
-
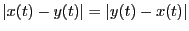 より
より
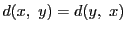 ,
,
- (iv)
-
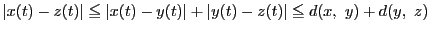 .
.
よって
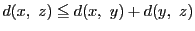 .
.
定理 71
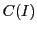
は距離
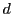
に関して完備である.
■
証明
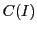 の基本列
の基本列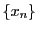 をとる.
つまり任意の正数
をとる.
つまり任意の正数 に対して
に対して
となる が存在するとする.
ところがこのとき任意の
が存在するとする.
ところがこのとき任意の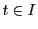 に対して
に対して
が成立するので,関数列として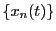 はコーシー関数列(定義17)である.したがって定理30によって
関数列
はコーシー関数列(定義17)である.したがって定理30によって
関数列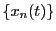 は定義域を
は定義域を とするある連続関数
とするある連続関数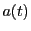 に一様収束する.
に一様収束する.
すなわち任意の正数 に対し
に対し
となる が存在する.よって
が存在する.よって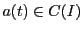 で
で
が成立する.つまり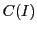 の点列
の点列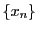 は
は に収束する.
つまり
に収束する.
つまり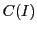 は完備である.
□
は完備である.
□


 次: 不動点定理
上: 次元の拡大
前: 次元の拡大
次: 不動点定理
上: 次元の拡大
前: 次元の拡大
2014-05-23
![]() の
の![]() 個の直積である
個の直積である![]() を考えなければならない.
を考えなければならない.![]() は加法や実数倍の演算が定義されベクトル空間となるが,さらに,ここに距離を入れ
は加法や実数倍の演算が定義されベクトル空間となるが,さらに,ここに距離を入れ![]() 次元ユークリッド空間として
次元ユークリッド空間として![]() を考えなければならない.距離というもの,およびそれと一体である内積の一般的な定義については『線型代数の考え方』を見てほしい.ここでは実数
を考えなければならない.距離というもの,およびそれと一体である内積の一般的な定義については『線型代数の考え方』を見てほしい.ここでは実数![]() 個の直積
個の直積![]() である
である![]() 次元ベクトル空間に距離を次のように定義する.
次元ベクトル空間に距離を次のように定義する.
![]() の二つの要素
の二つの要素
![]() と
と
![]() に対し,距離
に対し,距離
![]() を
を
![]() に対し,正の実数
に対し,正の実数![]() を用いて条件
を用いて条件
![]() の点の集合
の点の集合![]() が有界であるとは,
が有界であるとは,
![]() のすべての要素を含む超球が存在することとする.
のすべての要素を含む超球が存在することとする.
![]() 内の曲がった管や滑らかな物体
内の曲がった管や滑らかな物体![]() における流体や電磁場を微積分学を用いて解析する数学手法のことである.ベクトル解析は電磁場の理論を明確に述べるために開発され,物理学や工学等への応用が多い.ここでは後に必要なことにかぎって,その基本部分を構成しておきたい.
における流体や電磁場を微積分学を用いて解析する数学手法のことである.ベクトル解析は電磁場の理論を明確に述べるために開発され,物理学や工学等への応用が多い.ここでは後に必要なことにかぎって,その基本部分を構成しておきたい.
![]() 次元の場合に拡張しなければならない.しかしそれは,
次元の場合に拡張しなければならない.しかしそれは,![]() の場合に絶対値をもとに行ってきた諸々のことを,距離
の場合に絶対値をもとに行ってきた諸々のことを,距離![]() に置きかえて遂行すればよい.
に置きかえて遂行すればよい.
![]() のとき成分で表し
のとき成分で表し
![]() ,
,
![]() とすると,
とすると,
![]() 座標の集合は有界なので収束部分列がある.
その収束部分列を
座標の集合は有界なので収束部分列がある.
その収束部分列を![]() 座標とする部分点列の
座標とする部分点列の![]() 座標の集合も有界なので収束部分列をもつ.
同様の操作を順次行うと
座標の集合も有界なので収束部分列をもつ.
同様の操作を順次行うと![]() 座標の収束部分列が得られる.
この部分列に対応する部分点列において,
その
座標の収束部分列が得られる.
この部分列に対応する部分点列において,
その
![]() 座標はそれぞれ途中で構成した部分列の
部分列だから同じ値に収束し,その結果部分点列も収束する.
□
座標はそれぞれ途中で構成した部分列の
部分列だから同じ値に収束し,その結果部分点列も収束する.
□
![]() の点の集合
の点の集合![]() が閉集合であるとは,
が閉集合であるとは,
![]() に対して,
に対して,![]() を含むすべての閉集合の交わりを
を含むすべての閉集合の交わりを![]() の閉包といい
の閉包といい
![]() と表す.
と表す.
![]() が
が![]() で連続であることは次の条件とも同値である.
で連続であることは次の条件とも同値である.
![]() 内の
内の![]() に収束する任意の点列
に収束する任意の点列
![]() に対して
に対して
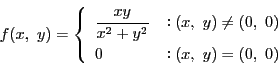
![]() を
を![]() に固定しこの方向から原点に近づくと
に固定しこの方向から原点に近づくと
![]() は原点では連続でない.
変数が多くなると連続性でもこのように複雑になる.
は原点では連続でない.
変数が多くなると連続性でもこのように複雑になる.
![]() が有界閉集合なので
が有界閉集合なので![]() の部分列
の部分列
![]() で
で
![]() の点
の点![]() に収束するものが存在する.
に収束するものが存在する.![]() が連続であるから
が連続であるから
![]() で考えた.
複雑な閉区間は考えていない.
二変数となると定義領域
で考えた.
複雑な閉区間は考えていない.
二変数となると定義領域![]() についての考察がさらに難しくなる.
次のような形の定理は,一変数の場合から明らかであるが,
についての考察がさらに難しくなる.
次のような形の定理は,一変数の場合から明らかであるが,
![]() が複雑な場合は難しい.
が複雑な場合は難しい.
![]() 変数でもまったく同様なので二変数の場合に述べる.
変数でもまったく同様なので二変数の場合に述べる.
![]() が
が
![]() 内を通る連続曲線
内を通る連続曲線![]() (定義35参照)で結ばれているとする.
(定義35参照)で結ばれているとする.
![]() である
である![]() に対して,
に対して,
![]() の間の曲線上の点
の間の曲線上の点![]() で
で
![]() となるものが存在する.
■
となるものが存在する.
■
![]() の点列
の点列![]() が点
が点![]() に収束するとは,
任意の正数
に収束するとは,
任意の正数![]() に対して,
に対して,
![]() で連続なとき,
で連続なとき,![]() は
は![]() で連続であるという.
■
で連続であるという.
■
![]() が
が![]() で連続であれば
で連続であれば
![]() に収束する
に収束する![]() の点列
の点列![]() に対し
に対し
![]() に収束する
に収束する![]() の点列
の点列![]() に対し
に対し
![]() の閉集合,開集合も定義される.
つまり
の閉集合,開集合も定義される.
つまり
![]() の点の集合
の点の集合![]() が閉集合であるとは,
が閉集合であるとは,
![]() に対して,
に対して,![]() を含むすべての閉集合の交わりを
を含むすべての閉集合の交わりを![]() の閉包といい
の閉包といい
![]() と表す.
と表す.
![]() で定義された連続関数の集合を
で定義された連続関数の集合を![]() とする.
とする.
![]() の変数を
の変数を![]() で表す.
で表す.
![]() の要素は関数であるがこれを
の要素は関数であるがこれを![]() のように表す.
のように表す.
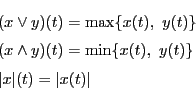
![]() に対し
に対し
![]() であり,
区間
であり,
区間![]() における最大値が存在する.
そこで,
における最大値が存在する.
そこで,![]() に実数値関数
に実数値関数![]() を次のように定義する.
を次のように定義する.
![]() は
は![]() における距離関数である.実際
における距離関数である.実際
![]() ,
,
![]() .
.
![]() に対し
に対し