![]()
中心を z とする.
![]()

図1のように
とする.
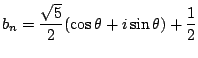 とおく.
とおく.
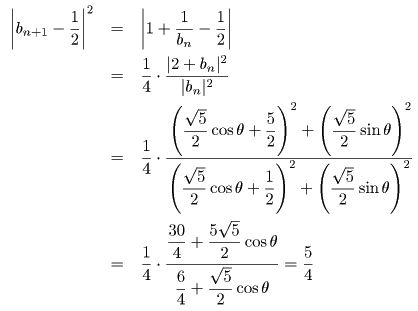
帰納法によりすべての
![]() が円 C 上にあることが示された.
が円 C 上にあることが示された.
[(2)の別解]
1次分数変換であるから,次のようにもできる.

東大理系前期4 問題 解説 2001年入試に戻る
![]()
中心を z とする.
![]()

図1のように
とする.
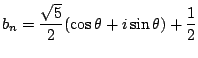 とおく.
とおく.
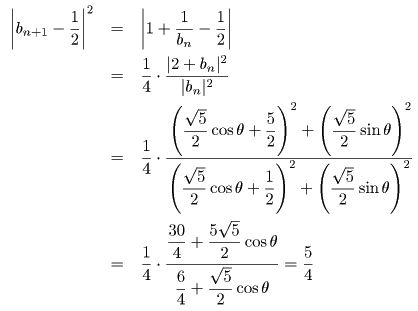
帰納法によりすべての
![]() が円 C 上にあることが示された.
が円 C 上にあることが示された.
[(2)の別解]
1次分数変換であるから,次のようにもできる.
