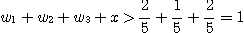東大理系前期5　問題　解説　2001年入試に戻る

　x リットルの水の入ったビーカーを A とする．

(1) 背理法で示す． 最後まで A の水量が x のままであったとする． 最後にビーカーが2つになる直前を考える． そのときの他の水量を $y,\ z\ (y\le z)$ とする． $x<\dfrac{1}{3}$ で x+y+z=1 であるから， x<z である．ゆえにありうる量の関係は
\begin{displaymath}x<y<z,\ x=y<z,\ x<y=z,\ y<x<z,\ y=x<z \end{displaymath}

しかしいずれの場合も A の水量は変化する．つまり 最後まで A の水量が x のままであることはない．


(2) 背理法で示す． 途中で A が空になるか，水量が増えたとする．

(a) A が空になる場合．その直前に少なくとも3つのビーカーがあり， A の水量が最小であった．つまり他の水量を 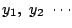$y_1,\ y_2\ \cdots$ とすると
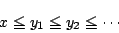
\begin{displaymath}x\le y_1\le y_2\le \cdots \end{displaymath}
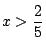である． $x>\dfrac{2}{5}$ よりこの場合
\begin{displaymath}x+y_1+y_2+\cdots>\dfrac{6}{5} \end{displaymath}
となり水量の総和が1と矛盾．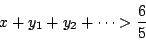

(b) 途中で増える場合．その直前に少なくとも3つのビーカーがあり， A の水量が2番目に小さかった．同様の理由で A 以上の水量の ビーカーが1つある． 最初 A の水量が最大であったので，この操作のどこかで A の水量が 最大でなくなっている． その直前の水量を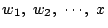 $w_1,\ w_2,\ \cdots,\ x$ とすれば
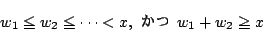
\begin{displaymath}w_1\le w_2\le \cdots <x,\ かつ\ w_1+w_2\ge x \end{displaymath}
この時点でビーカーは4つ以上ある （3つなら A の水量は変化しない）．

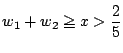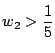$w_1+w_2\ge x>\dfrac{2}{5}$なので $w_2>\dfrac{1}{5}$ である．したがって  

\begin{displaymath}w_3\ge w_2 \end{displaymath}
より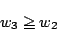

となり水量の総和が1と矛盾． したがって A の水量は最後まで x のままである．