2.

次: 3. 上: 2. 解答前: 1.

2.

別解2

(1) $\bigtriangle上 {\rm ABC}$ の各頂角を $\alpha,\ \beta,\ \gamma$ と置く．また $\bigtriangle上 {\rm ABC}$ を $\mathrm{A}(1,\ 0)$ として座標平面上において一般性を失わない．このとき鋭角三角形でも鈍角三角形でも $\mathrm{B}(\cos 2\gamma,\ \sin 2\gamma)$ , $\mathrm{C}(\cos 2(\gamma+\alpha),\ \sin 2(\gamma+\alpha))$ となる．

$\begin{eqnarray*}\mathrm{AB}^2+\mathrm{BC}^2+\mathrm{CA}^2&=& (\cos 2\gamma -1... ...+\alpha)\}\\ &=&8-8\cos(\gamma+\alpha)\cos\gamma \cos\alpha \end{eqnarray*}$
ゆえに AB²+BC²+CA²>8 は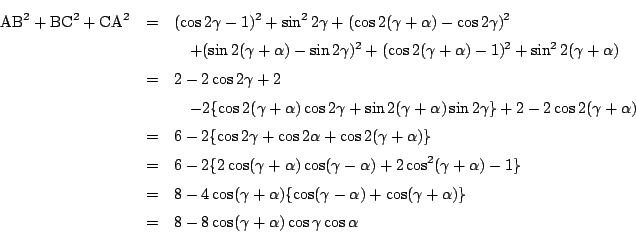 $\cos(\gamma+\alpha)\cos\gamma \cos\alpha<0$ を意味する．三角形の内角なので $\alpha,\ \gamma$ がともに $\alpha,\ \gamma\ge\dfrac{\pi}{2}$ となることは起こらない． $\alpha\ge\dfrac{\pi}{2}$ または $\gamma\ge\dfrac{\pi}{2}$ なら $\pi>\gamma+\alpha\ge\dfrac{\pi}{2}$ となり $\cos(\gamma+\alpha)\cos\gamma \cos\alpha\ge 0$ ．ゆえに $\cos(\gamma+\alpha)\cos\gamma \cos\alpha<0$ となるのは

$\begin{displaymath}0<\alpha,\ \gamma<\dfrac{\pi}{2},\ \dfrac{\pi}{2}<\gamma+\alpha<\pi \end{displaymath}$

$\beta=\pi-(\gamma+\alpha)$ なので，3つの頂角はいずれも鋭角である．
(2) (1)から $\bigtriangle上 {\rm ABC}$ が鋭角三角形のときに示せば十分である．与不等式を示すためには， $-1 \le 8\cos(\gamma+\alpha)\cos\gamma \cos\alpha$ が成り立つことを示せばよい． $\gamma$ を固定して

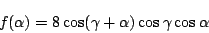
$\begin{displaymath}f(\alpha)=8\cos(\gamma+\alpha)\cos\gamma \cos\alpha \end{displaymath}$

と置く．このとき

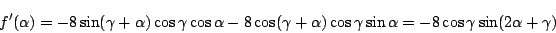
$\begin{displaymath}f'(\alpha)=-8\sin(\gamma+\alpha)\cos\gamma \cos\alpha -8\co... ...ha)\cos\gamma \sin\alpha =-8\cos\gamma\sin(2\alpha+\gamma) \end{displaymath}$

$\bigtriangle上 {\rm ABC}$ が鋭角三角形なので $\cos\gamma>0$ である． $0<2\alpha+\gamma<2\pi$ なので $2\alpha+\gamma=\pi$ のとき $f(\alpha)$ は極小かつ最小になる． $\alpha=\dfrac{\pi-\gamma}{2}$ より

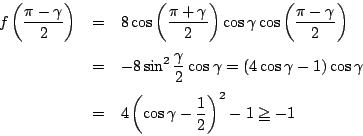
$\begin{eqnarray*}f \left(\dfrac{\pi-\gamma}{2}\right) &=&8\cos\left(\dfrac{\pi... ...gamma\\ &=&4 \left(\cos\gamma-\dfrac{1}{2} \right)^2-1\ge-1 \end{eqnarray*}$
等号成立は $\cos\gamma=\dfrac{1}{2}$ つまり $\gamma=\dfrac{\pi}{3}$ ．このとき $\alpha=\beta=\dfrac{\pi}{3}$ ．よって等号が成立するのは $\bigtriangle上 {\rm ABC}$ が正三角形のとき．

注意　本命題は四面体の場合にも次の形で成り立つ．
半径1の球面上に相異なる4点 A，B，C，D がある． \[ \mathrm{AB}^2+\mathrm{AC}^2+\mathrm{AD}^2+\mathrm{BC}^2+\mathrm{BD}^2+\mathrm{CD}^2\leqq 16 　…③ \] が成立する．

証明　記号は同様とする． \begin{eqnarray*} &&\mathrm{AB}^2+\mathrm{AC}^2+\mathrm{AD}^2+\mathrm{BC}^2+\mathrm{BD}^2+\mathrm{CD}^2\\ &=&3\left(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2+|\overrightarrow{c}|^2+|\overrightarrow{d}|^2 \right) -2( \overrightarrow{a}\cdot\overrightarrow{b}+ \overrightarrow{a}\cdot\overrightarrow{c}+ \overrightarrow{a}\cdot\overrightarrow{d}+ \overrightarrow{b}\cdot\overrightarrow{c}+ \overrightarrow{b}\cdot\overrightarrow{d}+ \overrightarrow{c}\cdot\overrightarrow{d})\\ &=&12-\left(\left|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\right|^2-4 \right)\\ &=&16-\left|\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\right|^2 \end{eqnarray*} これより， $ ③ $ が成立し，等号成立は， \[ \overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{0} \] のとき．四面体において，重心と外心が一致するのは，等面四面体のときである．『数学対話』－「特別な四面体」－「等面四面体」
http://aozoragakuen.sakura.ne.jp/taiwa/taiwaNch03/simentai/node8.html
を参考のこと．

AozoraGakuen
2002-03-01