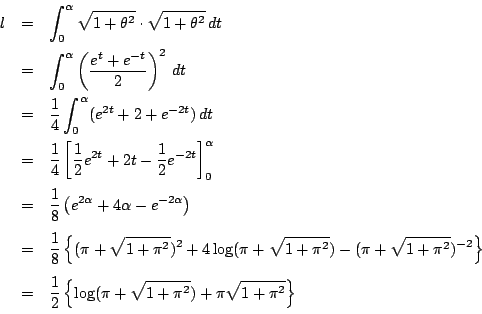次: 5.
上: 2. 解答
前: 3.
次: 5.
上: 2. 解答
前: 3.
-
- (1)
- (2)
曲線を,極座標の極を原点,始線を x 軸の正の部分にあわせて
xy 座標平面におく.このとき極座標で
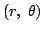 と表される点は
xy 座標では
と表される点は
xy 座標では
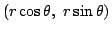 となる.
曲線の方程式は
となる.
曲線の方程式は 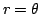 なので,この曲線はxy 座標では媒介変数
なので,この曲線はxy 座標では媒介変数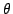 によって
によって
と表される.
ここで
したがって求める長さを l とすると
(1)より
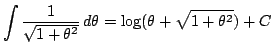 なので
なので
別解
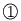 の計算は
の計算は
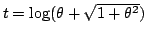 と変数変換してもよい.
このとき
と変数変換してもよい.
このとき
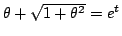 なので,
なので,
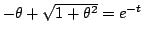 となる.
となる.
また(1)から
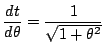 ,つまり
,つまり
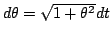 .
積分域は
.
積分域は
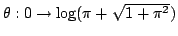 となるので
となるので
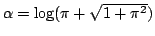 とおく.
とおく.
AozoraGakuen
2002-03-01
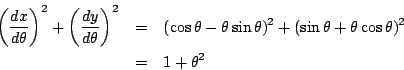
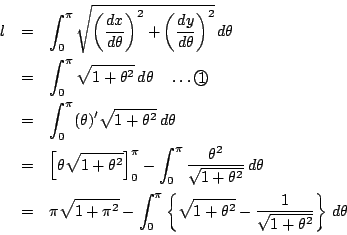
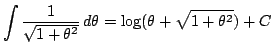 なので
なので
![\begin{eqnarray*}l&=&\pi\sqrt{1+\pi^2}-l+ \left[\log(\theta+\sqrt{1+\theta^2}) \...
...]_0^{\pi}\\
&=&\pi\sqrt{1+\pi^2}-l+\log(\pi+\sqrt{1+\pi^2})
\end{eqnarray*}](images/img81.gif)
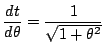 ,つまり
,つまり
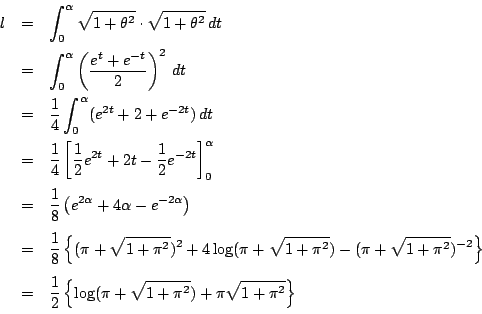
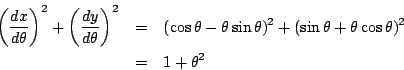
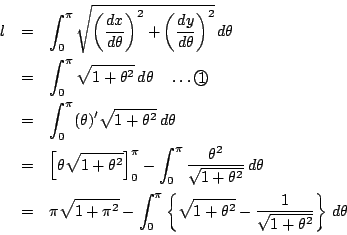
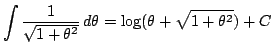 なので
なので
![\begin{eqnarray*}l&=&\pi\sqrt{1+\pi^2}-l+ \left[\log(\theta+\sqrt{1+\theta^2}) \...
...]_0^{\pi}\\
&=&\pi\sqrt{1+\pi^2}-l+\log(\pi+\sqrt{1+\pi^2})
\end{eqnarray*}](images/img81.gif)
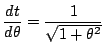 ,つまり
,つまり