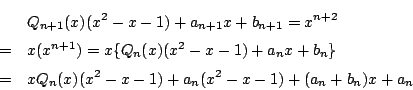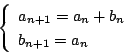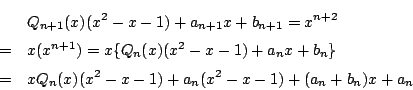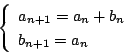(1)
xn+1 を x2-x-1 で割った商を Qn(x) とすると,各 n に対して
xn+1=Qn(x)(x2-x-1)+anx+bn
となる.したがって
割り算の一意性より,
an+1x+bn+1=(an+bn)x+an
これは恒等式であるから係数を比較して,
が成立する.
(2)
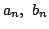 が共に互いに素な正の整数であることを数学的帰納法で示す.
が共に互いに素な正の整数であることを数学的帰納法で示す.
x2=x2-x-1+(x+1)
より
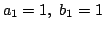 .ゆえに n=1 のとき,成立する.
n のとき成立するとする.
(1)より
.ゆえに n=1 のとき,成立する.
n のとき成立するとする.
(1)より
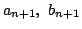 は正の整数である.
は正の整数である.
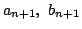 の最大公約数を d とし,
の最大公約数を d とし,
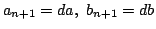 とおく.
(1)より
とおく.
(1)より
なので, d は 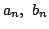 の公約数である.
帰納法の仮定から
の公約数である.
帰納法の仮定から 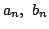 は互いに素なので, d=1 .つまり
は互いに素なので, d=1 .つまり
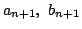 も互いに素である.
したがって n+1 のときにも成立する.
ゆえに,一般に自然数 n に対して題意が成立することが示された.
も互いに素である.
したがって n+1 のときにも成立する.
ゆえに,一般に自然数 n に対して題意が成立することが示された.