次: 4.
上: 2. 解答
前: 2.
次: 4.
上: 2. 解答
前: 2.
xyz空間の平面 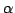 とその上にない点
とその上にない点
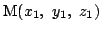 との距離を求める.
平面
との距離を求める.
平面 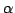 と直交するベクトル
と直交するベクトル
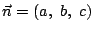 をとる.
また
をとる.
また 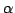 上の点
上の点
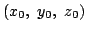 をとる.このとき
をとる.このとき 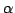 は
は
a(x-x0)+b(y-y0)+c(z-z0)=0
を満たす点
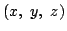 の集合である.
d=-(ax0+by0+cz0) とおき
の集合である.
d=-(ax0+by0+cz0) とおき 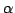 を
を
ax+by+cz+d=0
と表す.
点
M から平面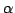 への垂線の足を
への垂線の足を
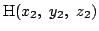 とする.
とする.
とかける.
この
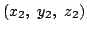 は
は 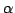 上の点なので
上の点なので
ax2+by2+cz2+d=0
つまり
t(a2+b2+c2)+ax1+by1+cz1+d=0
ゆえに
さて球面 S は
x2+y2+z2=1
と表される.点
Pの座標を
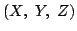 とする.
OP を直径とする球面は
とする.
OP を直径とする球面は
つまり
x2-Xx+y2-Yy+z2-Zz=0
と表される.ゆえに S との交わりの平面 L は両式を満たす点の集合なので
L:Xx+Yy+Zz-1=0
ゆえに
したがって条件
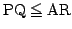 は
は
と同値である.
点
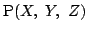 は S の外部にあるので
X2+Y2+Z2-1>0
したがってこの不等式は
は S の外部にあるので
X2+Y2+Z2-1>0
したがってこの不等式は
つまりS の外部で,かつ
である.ところがSと球体 の表面球とは半径の差が
中心間の距離に等しいので
の表面球とは半径の差が
中心間の距離に等しいので が S に内接し, S の外部で
が S に内接し, S の外部で を満たす点は
接点
を満たす点は
接点
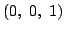 以外にない.
したがって V は
以外にない.
したがって V は を満たし,かつ S の外部となる点の集合である.
その体積は
を満たし,かつ S の外部となる点の集合である.
その体積は
AozoraGakuen
2002-03-01