これをいいかえれば,1点を共有するか平行であるかを区別しなくてよい一般的な立場や方法があるということである.それはまた,円や楕円など個別の円錐曲線をそれがおかれた平面の変換で互いにうつすことができ,直線が束をなすという性質,あるいは点が共線であるという性質が,その変換で変わらない.そのような平面とその変換があるということでもある.
これらを実際に構築する方法は,これまでの考察でも垣間見えてきているわけであるが,今後の課題である.ただこのような立場,あるいはこのような幾何ができたならば,平行な場合を区別しなくてよいし,円の場合に証明すればよいことになる.
そこでまず,円の場合のパスカルの定理である命題1 について, その証明をいろいろと考えていこう.そしてそこで使われる方法を吟味し, 証明の根拠としてどのような理論が準備されればならないのかを考えよう.
その手持ちの方法を,日本の高校数学の方法とすることは自然である.ところが,日本の高校数学で使えることが国家の方針によってよく変更される.例えば,複素平面は2010年現在は教育課程に入っていない.しかし10年前にはあり,2012年入学年から復活する.逆にそのとき,二次行列や平面の一次変換はなくなる.しかしこのように教育課程が定まらないことはたいへん大きな問題であり,不幸なことである.
15歳から18歳の時代に学んでおくべきことはそんなに変化するものではない.それをこの間青空学園では一貫して訴えてきた.そこでこの節で使う方法を,これまで日本の高校数学に現れた次のものを大きくは越えない次のものとする. この範囲のうちで『円錐曲線試論』に現れた諸命題の証明を試みよう.
円周上に6点A,B,C,D,E,F がこの順にある.命題1は
![]() 等のあらゆる型に対し,つねにパスカル線が定まることを主張している.このうちの一つの場合
等のあらゆる型に対し,つねにパスカル線が定まることを主張している.このうちの一つの場合
![]() について,円周角の相等と三角形の相似を用いて命題1を示そう.
について,円周角の相等と三角形の相似を用いて命題1を示そう.
命題1に,点の順も条件としてつけ加えた次の命題で示す.
 証明
3点A,D,P を通る円を
証明
3点A,D,P を通る円を
この結果,
![]() と
と
![]() は相似であり,点Rが相似の中心である.
よって他の頂点P,Qと相似の中心Rは共線である.
□
は相似であり,点Rが相似の中心である.
よって他の頂点P,Qと相似の中心Rは共線である.
□
 長さの比を用いる証明
長さの比を用いる証明
平面上に直線![]() がある.
がある.![]() 上には1の大きさと正の方向が定まっているものとする.2点
上には1の大きさと正の方向が定まっているものとする.2点
![]() がある.このとき,点Aから点Bへ向かう方向が,定まっている正の方向のとき「AB」でAとBの距離を正の値にとった数を表す.点Aから点Bへ向かう方向が,定まっている正の方向と逆のとき「AB」でAとBの距離を負の値にとった数を表す.符号をつけた線分を有向線分という.その値を「有向線分の長さ」という.混乱しないときは「有向線分」で長さも表すことがある.
がある.このとき,点Aから点Bへ向かう方向が,定まっている正の方向のとき「AB」でAとBの距離を正の値にとった数を表す.点Aから点Bへ向かう方向が,定まっている正の方向と逆のとき「AB」でAとBの距離を負の値にとった数を表す.符号をつけた線分を有向線分という.その値を「有向線分の長さ」という.混乱しないときは「有向線分」で長さも表すことがある.
![]() 上の3点
上の3点
![]() がどの順で並んでいても
がどの順で並んでいても
今後用いるのは
![]() のような比である.この比の値は
のような比である.この比の値は![]() の正の方向をいずれにとるかに関係なく一意に定まる.比の値が正ということは同方向,負ということは逆方向であることを意味する.以下直線上の線分の長さの比をこの意味で用いる.
の正の方向をいずれにとるかに関係なく一意に定まる.比の値が正ということは同方向,負ということは逆方向であることを意味する.以下直線上の線分の長さの比をこの意味で用いる.
 (1)
(1)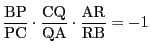 となる.
となる.
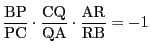 なら
3点
なら
3点
(1)をメネラウスの定理といい,(2)をメネラウスの定理の逆という.あわせて,条件
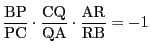 と,3点が1直線上にあるという条件が,同値であるということである.
と,3点が1直線上にあるという条件が,同値であるということである.
 (1)
(1)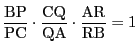 が成立する.
が成立する.
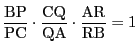 なら
3直線
なら
3直線
(1)をチェバの定理といい,(2)をチェバの定理の逆という.あわせて,条件
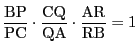 と3直線が1点で交わることが同値であるということである.
と3直線が1点で交わることが同値であるということである.
メネラウスの定理の証明
 (1)
点
(1)
点![]() から
から![]() に平行な
直線
に平行な
直線![]() を引く.
を引く.
(2)
直線![]() と直線
と直線![]() の交点を
の交点を
![]() とする.
このとき
とする.
このとき
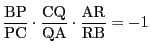 なので
なので
チェバの定理の証明
(1)
![]() を直線
を直線![]() が切っていると見れば,メネラウスの定理から
が切っていると見れば,メネラウスの定理から
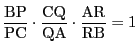 なので
なので
証明
直線![]() と
と![]() の交点を
の交点を![]() ,
直線
,
直線![]() と
と![]() の交点を
の交点を![]() ,
直線
,
直線![]() と
と![]() の交点を
の交点を![]() とする.
とする.
![]() と直線
と直線![]() にメネラウスの定理を用いて
にメネラウスの定理を用いて
 これら3式をかけあわせ,方べきの定理
これら3式をかけあわせ,方べきの定理
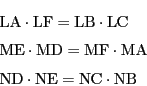
さらに次のような問題も指摘できる. パスカルは円を底面とする円錐を切断することで,円の場合にパスカル線の存在を示せば,円錐曲線の場合も証明されていることを指摘した.
この方法で底面上の線分は円錐を切断する平面上の線分に対応するが,その長さは変化するし,同じ直線上の線分の比も変化する.一方,メネラウスの定理やチェバの定理では,線分の長さおよびその比が重要であった.
長さや比を用いて円の場合に証明する.それを長さや比を保たない変換で円錐曲線に一般化するのだから,円の場合の証明がそのまま円錐曲線の場合の根拠となるのか,吟味も必要になる.この証明方法では,このような問題が生じる.