をこれら4点の複比といい,
複比は点がどのように並んでいるかに関係なく定義される.
逆にいいかえると,
直線上にある4点
![]() に関して,
点そのものは動かさず,点名
に関して,
点そのものは動かさず,点名
![]() の24通りの順列に対応して,その順列を「あ,い,う,え」とすると,
複比
の24通りの順列に対応して,その順列を「あ,い,う,え」とすると,
複比
![]() が定まり,合計24個の複比が定義される.
が定まり,合計24個の複比が定義される.

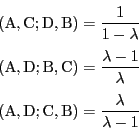
複比は6個の値のどれかで一致すれば,おなじ並べ替えを行った他の値でも一致することがわかる.またこれら6個の値のなかに同じものが現れるのは実数の範囲では
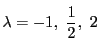 のときである.現在はユークリッド平面で考えている.複素解析など複素数平面で考えるとさらに
のときである.現在はユークリッド平面で考えている.複素解析など複素数平面で考えるとさらに
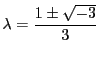 ,つまり1の6乗根が現れる.
,つまり1の6乗根が現れる.
![]() のときは
のときは
![]() が
が![]() となる.
となる.
![]() のとき4点A,B,C,Dは調和列点をなすという.
またこのとき,
のとき4点A,B,C,Dは調和列点をなすという.
またこのとき,
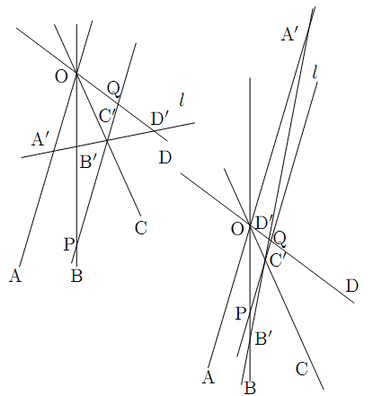
証明 $ l $ を動かすが,$ l $ の平行移動によって 複比
 点
点![]() をとおり直線
をとおり直線![]() に平行な直線を引き,
に平行な直線を引き,
![]() ,
,![]() との交点をP,Qとする.
との交点をP,Qとする.
複比は点![]() と直線で決まるので,
これを
と直線で決まるので,
これを
![]() と記す.点
と記す.点![]() を記さず
を記さず
![]() と記すときは4点は同一の直線上にあるときである.また,上記図の右の場合のように,直線
と記すときは4点は同一の直線上にあるときである.また,上記図の右の場合のように,直線![]() の交点は点
の交点は点![]() に関して同じ側にある必要はない.
に関して同じ側にある必要はない.
証明 点PとQが4点の優弧,劣弧に関して同じ側にあれば 円周角の相等により
点PとQが4点のうちの2点に関して優弧,劣弧の異なる側にある場合は, 点Qに関する角を補角にとることによって, 補題4から二つの複比の相等が結論される. □
証明
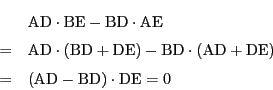
証明 2直線
 証明
新たに,直線APと直線DRの交点をL,直線QBと直線FAの交点をUとする.
補題5によって
証明
新たに,直線APと直線DRの交点をL,直線QBと直線FAの交点をUとする.
補題5によって
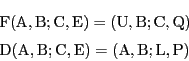
改めてパスカルの補題Iを命題として掲げる.
命題 3
M,S,Qで定まる平面上で,点Mから2直線MK,MVを,また点Sから2直線SK,SVを引く.点Kを直線MK,SKの交点,点Vを直線MV,SVの交点,点Aを直線MK,SVの交点,点![]() を直線MV,SKの交点とする.
を直線MV,SKの交点とする.
 4点A,K,
4点A,K,![]() ,Vのうちの2点でMやSとあわせた3点が同一直線上にないもの,例えばK,Vをとり,その2点を通る円を描き,それが直線MV,MK,SV,SKを切る点をO,P,Q,Nとすれば,直線MS,NO,PQは,同じ束をなす.
■
,Vのうちの2点でMやSとあわせた3点が同一直線上にないもの,例えばK,Vをとり,その2点を通る円を描き,それが直線MV,MK,SV,SKを切る点をO,P,Q,Nとすれば,直線MS,NO,PQは,同じ束をなす.
■
証明
直線PQと直線KNの交点をL,
直線AMと直線NOの交点をTとする.
補題5によって
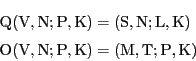
補題7によって3直線MS,TN(![]() ON),PL(
ON),PL(![]() PQ)は束をなす.
□
PQ)は束をなす.
□
円周上の6点A,B,C,D,E,Fに対して,型に対して,5点
をとる.複比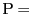
,
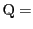
,
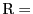
,
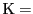
,
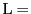
をとる.直線上の点
をとれば
直線上の点
をとれば
よって
これから,
,
は束をなし, この結果,3点
は共線である.
この論の展開は,6点A,B,C,D,E,Fの並び方には関係なく成立する.つまりこれで円周上の6点に関するパスカルの命題1が,交点
![]() が存在する場合に,一般的に証明された.
が存在する場合に,一般的に証明された.
しかし,ユークリッド幾何と複比の方法は,パスカルの円錐曲線論のなかでの方法としては,統一性がない.パスカルは直線の集合が平面上の1点を共有する場合と平行な場合を区別しない.それに対して補題4の証明では平行線の性質を用いた.また補題5の証明では円周角の定理と図形の移動を用いている.すべてユークリッド幾何の範囲であり,パスカルの方法との統一性はない.
これをどのように解決するか.われわれはあと一息で射影幾何というところまできている.新しい幾何を見出さなければならない.新しい対象と,それとの統一性をもった論証の方法を組み立てなければならない.そのためには,複比とそれが線束を切る直線![]() のとり方によらないことについての掘りさげた考察が必要である.こうしてパスカルの定理を証明する統一性が浮かんでくる.これを掘りさげ,新しい幾何を見出していこう.
その前に,パスカルの定理のさらにいくつかの証明を考える.
のとり方によらないことについての掘りさげた考察が必要である.こうしてパスカルの定理を証明する統一性が浮かんでくる.これを掘りさげ,新しい幾何を見出していこう.
その前に,パスカルの定理のさらにいくつかの証明を考える.