パスカルの方法で構成したモデルはあくまでユークリッド座標空間,正確にはアフィン空間を根拠としている.ユークリッド平面の直線を類別して射影平面の点を得た.これはユークリッド座標空間を基礎にしている.射影空間をそれ自身として定義することはできないのか.
公理をてこに論を展開すること自体が,現象としての数学をとらえることの深まりそのものとなる.公理は仮説である.物理学も仮説を設定する.しかし仮説の検証方法は,数学と物理学とでは異なる.物理学は実験で検証される.数学では,矛盾なく数学的現象をとらえることができるかどうかで検証され,それ自体がまた数学的現象の構造を深く識ることになる.
確実なことを改めて取りあげ,そこから厳密な論証で射影幾何を再構成し,そのなかで複比をもういちど定義しなおし,そのうえでパスカルの定理の証明を試みるのでなければならない.そのときに複比の本質をとらえ直さなければならない.複比は本当に長さの比なのか.あるいはそれは外見であってその本質は長さという概念によらないものであるのか.
点と呼ばれるものの集合と直線と呼ばれるものの集合があり,それらのあいだにどのような関係が成り立っていれば射影幾何が定義されるのか.公理を立てる方法というのは,空間的で幾何的な直観を論理的に分析し,その内容を公理に定式化し,そこから論を展開しつつ,また公理そのものの分析を行うという,数学の方法である.
その場合,どのような公理系を設定するのかが重要な問題になる.関連するすべての命題の真偽を決定できるという公理の完全性,公理系のいくつかの公理から同じ公理系の他の公理が導かれることはないという公理の独立性,公理からある命題とその命題の否定が同時に導けることはないという公理の無矛盾性,公理系の設定ではこれらをめざすべきである.
われわれはパスカルの思想やその試論の証明をふりかえり,それを公理的方法でとらえ,そこから射影幾何を定式化することを試みよう.このような研究は十九世紀末から二十世紀初頭にかけてドイツやフランスを中心に行われ,そのからくりはほぼ解明され,まとめられてきた.これらを参考に,定義と公理を定め,基本的な証明を再構成するという方向で考えていきたい.そこで,先に定義した
![]() はいったんおき,改めてそれらの公理的定義を構成してゆこう.
はいったんおき,改めてそれらの公理的定義を構成してゆこう.
したがって,「関係」とは何かということをふくめて,公理の構造をより明確にするために,次のように言葉を定めることもできる.
二つの集合と
,および
と
の関係
が与えられている.集合の組
において,
が
となるとき,
が
の上にあるといい,
は
を通るという.
いかに於いては,関係![]() を省略し,集合の組を
を省略し,集合の組を![]() のように書くことが多い.
のように書くことが多い.
以上の準備によって次の公理系を述べることができる. 次の公理系がもっとも簡明でしかも論を述べるのに十分なものである, つまり,完全であり,独立であり,さらに,無矛盾であることも,体論などより基本的な体系の無矛盾性に還元して示されることが知られている. これらについては例えば『射影幾何学』[35]などを参照のこと.
定義 6
射影幾何の公理をみたす集合![]() と
と![]() の組
の組![]() を射影幾何,
を射影幾何,
![]() を射影空間という.
■
を射影空間という.
■

射影空間の点と直線を,ユークリッド平面の点や直線で考えるが,これはあくまで象徴的な記号として用いるのであって,ユークリッド平面におかれた図形の点や直線ではない.だから,いわゆる無限遠点もこの平面のなかに書いて考えることができる.そのことをふまえたうえでは,公理II)を図示することができる.
これに対して集合としての共通部分![]() を
を![]() の交わりという.
■
の交わりという.
■
証明
3点が共線で![]() 上にあれば
上にあれば
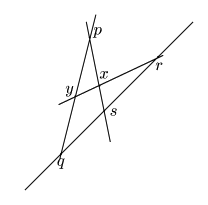 次に3点が共線でないとする.
任意の
次に3点が共線でないとする.
任意の
![]() をとる.点
をとる.点![]() が存在して
が存在して![]() .
もし
.
もし![]() または
または![]() なら
なら
![]() .
.
![]() かつ
かつ![]() とする.
公理II)を
とする.
公理II)を
で用いる.2直線![]() ,
,![]() は交わる.交点を
は交わる.交点を![]() とする.
とする.
![]() ,
,![]() より
より
![]() .つまり
.つまり
逆の包含関係も同様に成り立ち等号が成立する. □
命題 17
![]() と
と![]() が射影空間
が射影空間![]() の部分空間であるとき,
結び
の部分空間であるとき,
結び![]() は
は![]() と
と![]() を含む最小の部分空間である.
■
を含む最小の部分空間である.
■
![]() と
と![]() を含む部分空間は
を含む部分空間は![]() の直線をすべて含み,その結果
の直線をすべて含み,その結果![]() を含む.
つまり,
を含む.
つまり,![]() は
は![]() と
と![]() を含む最小の部分空間である.
□
を含む最小の部分空間である.
□
このことから![]() を
を![]() の張る空間ともいう.
の張る空間ともいう.
![]() 個の点
個の点
![]() があれば,
があれば,![]() の交換律と結合律によって,
部分空間
の交換律と結合律によって,
部分空間
 証明
証明
後に用語を定義するが,![]() は射影平面といわれる.この命題によって射影平面上の2直線は交わることが示された.これは,公理系からの結論なのである.
は射影平面といわれる.この命題によって射影平面上の2直線は交わることが示された.これは,公理系からの結論なのである.
証明
証明
逆に射影空間では
![]() が成立することを示す.
が成立することを示す.
![]() の直線
の直線![]() をとる.
をとる.
![]() は
は![]() の直線なので,
の直線なので,
![]() となる
となる![]() が存在する.
が存在する.
![]() で
で![]() は
は![]() の直線でもあるので,
の直線でもあるので,![]() 上の点は
上の点は![]() に含まれる.
つまり
に含まれる.
つまり![]() でもある.
よって
でもある.
よって![]() は
は
![]() の直線である.
の直線である.
よって命題が示された. □
命題20の結論部分に関して次のことが成り立つ.
 命題 21
二つの条件
命題 21
二つの条件
証明 それぞれ対偶を示す.
条件Qが成り立たないとする.つまりQの条件を満たす![]() が存在するとする.このとき
が存在するとする.このとき
条件Pが成り立たないとする.
![]() であるから,
であるから,
![]() は成立している,
よって
は成立している,
よって
![]() である.
である.
![]() ,
,
![]() とおく.
とおく.
射影幾何の公理という極めて単純な公理から, 部分空間の列に関するこのような命題が示された.
「束論」という分野がある. 命題21は束論の命題であり, 束論の表現を用いると「射影空間とその部分空間はモジュラー束をなす」ということになる. これについては『束論』[35],および『射影幾何学』[35]を参照されたい.
 命題 22
射影空間の二つの部分空間
命題 22
射影空間の二つの部分空間![]() と
と![]() がある.部分空間の二つの集合
がある.部分空間の二つの集合
証明
![]() ,
,![]() は明らかである.
は明らかである.
![]() ,
,![]() の可換性と命題20より,
の可換性と命題20より,
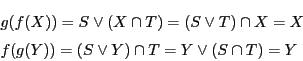
この対応は単に一対一対応であるばかりではなく,包含関係を保持する.
つまり,
![]() なら
なら
![]() .
.![]() も同様.したがって部分空間の集合を包含関係の構造をもつものと考えれば,この構造に関する同型写像になっている.
も同様.したがって部分空間の集合を包含関係の構造をもつものと考えれば,この構造に関する同型写像になっている.
またこれによって,![]() が
が![]() の上に素なら,
の上に素なら,![]() は
は![]() の上に素であり,その逆も成り立つ.
の上に素であり,その逆も成り立つ.
 例 3.1.2
次小節で射影空間の次元などを定義する.
それを前提にする.
例 3.1.2
次小節で射影空間の次元などを定義する.
それを前提にする.![]() ,
,![]() を直線とし,
を直線とし,
![]() とする.このとき
とする.このとき![]() は3次元射影空間である.
は3次元射影空間である.
![]() となる
となる![]() とは
とは![]() を含む平面(2次元射影空間)である.
この
を含む平面(2次元射影空間)である.
この![]() に対する
に対する![]() は
は![]() と
と![]() の交点である.
の交点である.
![]() となる
となる![]() とは
とは![]() 上の点である.
上の点である.
![]() は
は![]() と
と![]() を含む平面である.これが一対一対応の意味である.
を含む平面である.これが一対一対応の意味である.
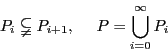
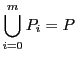 となる.
■
となる.
■
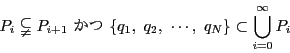
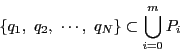
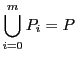 となる.
□
となる.
□
このように有限次元射影空間では,
![]() からはじまり
からはじまり![]() に至る部分空間の列は有限列になる.部分空間の列が有限であっても,その長さに最大値が存在するとはかぎらない.しかし射影幾何の公理のもとでは,公理IV)からこのような列の長さに最大値が存在することが帰結する.それを見てゆこう.
に至る部分空間の列は有限列になる.部分空間の列が有限であっても,その長さに最大値が存在するとはかぎらない.しかし射影幾何の公理のもとでは,公理IV)からこのような列の長さに最大値が存在することが帰結する.それを見てゆこう.
証明

![]() ならこれを
ならこれを![]() と見ることで,帰納法の仮定から成立.
と見ることで,帰納法の仮定から成立.
![]() とする.部分空間の列
とする.部分空間の列![]() を考える.
を考える.
![]() なので
なので
![]() は
は
![]() か
か![]() に一致.部分空間の列
に一致.部分空間の列![]() は順次上に素とはかぎらないが,さらに細分することを考えれば,
は順次上に素とはかぎらないが,さらに細分することを考えれば,![]() にはじまり
にはじまり![]() に終わる
に終わる![]() の列が
の列が![]() の系列と
の系列と
![]() の系列を必要ならさらに細分したものと二つできる.
の系列を必要ならさらに細分したものと二つできる.![]() は二つの長さのうち大きくない方であるので帰納法の仮定から,この二列の長さは等しい.
一方,これはまた
は二つの長さのうち大きくない方であるので帰納法の仮定から,この二列の長さは等しい.
一方,これはまた![]() にはじまり
にはじまり![]() に終わる二つの列でもあり,
に終わる二つの列でもあり,
![]() からなる列の長さは
からなる列の長さは![]() なのでやはり帰納法の仮定から
なのでやはり帰納法の仮定から![]() である.
よって
である.
よって![]() が成立し,この結果,命題が証明された.
□
が成立し,この結果,命題が証明された.
□
最大となるのは,![]() が1点からなる部分空間で,
が1点からなる部分空間で,![]() が
が![]() の上に素なときである.このとき,命題24よりその長さは部分空間列のとり方によらず一定である.
の上に素なときである.このとき,命題24よりその長さは部分空間列のとり方によらず一定である.
![]() のときこれを明記して
のときこれを明記して![]() とも記す.
明らかに各部分空間も有限次元である.
とも記す.
明らかに各部分空間も有限次元である.![]() 次部分空間を
次部分空間を![]() のように記す.
1点よりなる部分空間の次元は0,つまり
のように記す.
1点よりなる部分空間の次元は0,つまり![]() である.
直線の集合
である.
直線の集合![]() の要素はこれを部分射影空間とみると1次元であり,つまり
の要素はこれを部分射影空間とみると1次元であり,つまり![]() である.
これを射影直線という.また
である.
これを射影直線という.また![]() を射影平面という.
さらに,射影空間としての空集合は
を射影平面という.
さらに,射影空間としての空集合は
![]() とする.
その理由は次の次元定理が例外なく成立するようにするためであるが,
とする.
その理由は次の次元定理が例外なく成立するようにするためであるが,![]() の一つ前という点からいっても自然である.また
の一つ前という点からいっても自然である.また![]() 次元射影空間において
次元射影空間において![]() を超平面という.
を超平面という.
同じ![]() 次元射影空間で別のものを区別するときは,
次元射影空間で別のものを区別するときは,
![]() と
と![]() のように文字をかえることにする.
次元が関わらない命題では部分空間を
のように文字をかえることにする.
次元が関わらない命題では部分空間を![]() や
や![]() のように表す.
のように表す.
証明 それぞれの部分の順次上に素な部分空間の列を繋ぐことで,
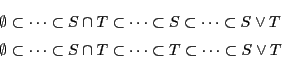
この結果
![]() なら
なら
また
![]() なら,
なら,
証明
証明
とすれば,射影幾何の公理から逆に図形とは何かを定義し直さなければならない.
すでにパスカルの思想にならって, ユークリッド空間の直線束の概念から射影空間を構成した. そして,そこで得られた性質を公理として定式化した. そのうえで,逆にその公理から図形と束を定義し直したのである.
公理I)について.
![]() をとる.命題27より
をとる.命題27より
![]() なので,
なので,
![]() となり,
となり,![]() をとおる
をとおる![]() の要素が存在した.
の要素が存在した.
公理II)について.
![]() での意味において共線でない
での意味において共線でない
![]() ,
および異なる
,
および異なる
![]() をとる.
をとる.
![]() において,
において,
![]() ,
,
![]() とする.
とする.
![]() とする.
とする.
![]() なので,
なので,
![]() .ゆえに
.ゆえに
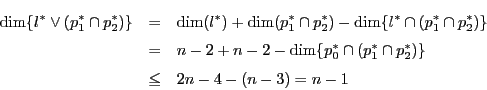
公理III)について.
![]() をとる.
をとる.![]() は
は![]() においては
においては![]() なので,
なので,
![]() に含まれない点
に含まれない点![]() ,
,![]() に含まれない点
に含まれない点![]() をとることができる.
射影幾何の公理1のIII)によって,
直線
をとることができる.
射影幾何の公理1のIII)によって,
直線![]() 上に第3の点
上に第3の点![]() が存在する.
が存在する.
![]() において
において
![]() とおくと,
とおくと,
![]() は
は![]() を含む超平面である.
これは
を含む超平面である.
これは![]() において
において![]() で,
で,
![]() での点
での点![]() が
が![]() での直線
での直線![]() 上にあることを意味している.
上にあることを意味している.
公理IV)について.
![]() の
の![]() 個の独立な点
個の独立な点
![]() をとる.
をとる.
さらにこれから![]() も
も![]() 次元であることがわかる.
□
次元であることがわかる.
□