

 次: 射影写像
上: 射影幾何の公理
前: 公理系を立てる
次: 射影写像
上: 射影幾何の公理
前: 公理系を立てる
このような公理系は,それを満たすものを構成しうることが重要である.それを与えるのがパスカルの思想を具体化した同次座標の方法である.
その端緒はすでに「パスカルの方法」のなかの「切断の方法」で述べた.
そこでは実数体の上に構成したのであるが,
以下はそれを必ずしも可換でない一般の体でそれを行おう.
ここで確認のため体の定義を掲げる.
ここで,体の定義を確認し,いくつかの重要なことを証明しておこう.
実数体の定義は『解析基礎』を,複素数体の定義は『数学対話』の「複素数の構成」を,
また有限体は『数論初歩』を参考にしてほしい.
集合 を考え,
を考え, や
や で
で の要素を表す.
集合
の要素を表す.
集合 が次の条件を満たすとき,体という.
が次の条件を満たすとき,体という.
- 2つの演算,加法
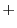 と乗法
と乗法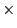 が定義されている.
つまり,
が定義されている.
つまり, の要素
の要素 や
や に対して,
要素
に対して,
要素
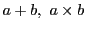 がそれぞれ確定する.
がそれぞれ確定する.
- 2つの演算は結合法則を満たす.
- 加法は可換である.
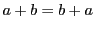 が成り立つ.
が成り立つ.
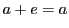 ,
,
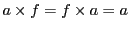 となる要素
となる要素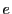 と
と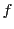 が存在する.
が存在する.
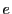 を加法の単位元といい,通常0と書く.
を加法の単位元といい,通常0と書く.
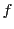 を乗法の単位元といい,通常1と書く.
を乗法の単位元といい,通常1と書く.
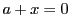 となる
となる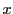 が存在する.
これを
が存在する.
これを の加法の逆元といい,
の加法の逆元といい,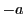 と書く.
と書く.
- 0でない要素
 に対して
に対して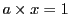 となる
となる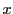 が存在する.
これを
が存在する.
これを の乗法の逆元といい,
の乗法の逆元といい,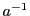 と書く.
と書く.
- 加法と乗法について分配法則が成り立つ.
乗法についても可換性
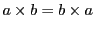 が成り立つものを可換体と呼ぶ.
が成り立つものを可換体と呼ぶ.
二つの体の間の一対一対応写像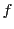 が演算を保存するとき,これを体の同型写像という.演算を保持するとは,
が演算を保存するとき,これを体の同型写像という.演算を保持するとは,
となることである.同型写像の集合は,写像の合成を演算として群をなす.
これを体 の同型群といい
の同型群といい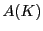 と表す.
と表す.
後に必要となる体論の命題をここに述べる.
 を体とし,
を体とし, を
を の0でない要素とする.
の0でない要素とする. から
から への写像で
への写像で
で定義されるものは, から
から への同型写像である.
これを
への同型写像である.
これを の内部自己同型という.
内部自己の集合は,写像の合成を演算として群をなす.
これを体
の内部自己同型という.
内部自己の集合は,写像の合成を演算として群をなす.
これを体 の内部自己同型群といい
の内部自己同型群といい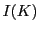 と表す.
と表す.
 が可換体なら内部自己同型は恒等写像のみである.
実数体や複素数体はもとより可換体であり,
内部自己同型群
が可換体なら内部自己同型は恒等写像のみである.
実数体や複素数体はもとより可換体であり,
内部自己同型群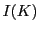 は恒等写像のみの群である.
は恒等写像のみの群である.
実数体や複素数体では,内部自己同型ではない他の同型に関して次の命題が成立する.
その証明は有理数体が実数体の中で稠密に存在するという,
実数の連続性に関わることを根拠にしている.
実数体の構成と連続性に関することは『解析基礎』にある.それを前提にする.
命題 29
実数体
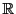
の同型写像群
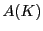
は恒等写像のみの群である.■
証明
恒等写像でない同型 が存在すると仮定する.
恒等写像ではないので
が存在すると仮定する.
恒等写像ではないので
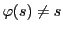 となる
となる
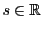 が存在する.
が存在する.
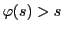 なら
なら
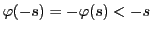 なので,
必要なら
なので,
必要なら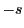 をとることによって
をとることによって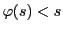 とできる.有理数体
とできる.有理数体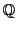 は実数体
は実数体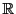 の中で稠密である.ゆえに
の中で稠密である.ゆえに
となる有理数 が存在する.
が存在する.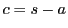 とおく.
とおく.
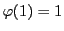 なので,
なので,
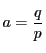 と整数
と整数 と
と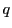 で表す.
正整数
で表す.
正整数 に関しては,
に関しては,
 が体の同型であることから
が体の同型であることから
となり,
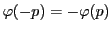 より負の整数も
より負の整数も で動かない.
これから
で動かない.
これから
となり, は
は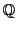 の要素を動かさない.よって
の要素を動かさない.よって
一方,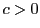 なので
なので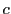 はある0でない実数
はある0でない実数 を用いて
を用いて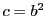 と表される.
よって
と表される.
よって
これは矛盾である.
□
体の超越拡大に関する準備を必要とするので,次の命題の証明は略する.
命題 30
複素数体
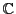
の同型群
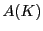
は無限群である.
そのうち複素数体の実数から導かれる位相に関して連続となるものは
複素共役写像
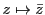
のみである.
■
以下 を体とする.
体上の線形空間とその基底については,代数学の基本書を参考にしてもらいたい.
を体とする.
体上の線形空間とその基底については,代数学の基本書を参考にしてもらいたい.
定義 16

を体,

を自然数とし,

個の

の要素の順序づけられた組
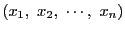
を考える.これを
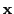
のようにも表す.
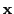
の集合を
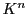
と書く.
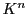
に加法と

の要素
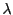
の

倍を次のように定める.
-
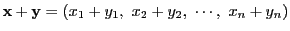
-
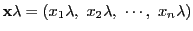
このように定めると
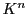
は加法群であり,かつ

の右からの作用をもつ.
つまり

右加群である.
これを

上の

次元右線形空間といい,
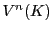
のように記す.
あるいは簡単のために
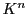
とすることもある.
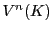 の部分集合
の部分集合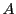 で,
で,
 の右からの積で閉じており,それ自身同様に
の右からの積で閉じており,それ自身同様に 右加群であり,
かつ
右加群であり,
かつ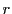 個よりなる基底が存在するものを
個よりなる基底が存在するものを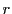 次元部分空間という.
■
次元部分空間という.
■
体 上の
上の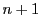 次元右線形空間の要素を
次元右線形空間の要素を
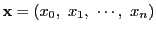 のように添え数を0からはじめるものとする.
のように添え数を0からはじめるものとする.
命題 31
体

上の
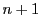
次元右線形空間
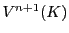
がある.
この1次元部分空間の集合を

,2次元部分空間の集合を
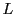
とし,
ある2次元部分空間がある1次元部分空間を含むことを「通る」とすれば,
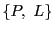
は射影幾何の公理I)〜IV)を満たす.
■
証明
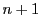 次元線形空間
次元線形空間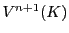 の
の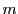 次元部分空間を
次元部分空間を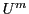 のように表す.
のように表す.
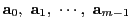 が
が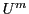 の基底であることを
の基底であることを
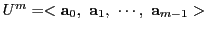 と表す.
と表す.
公理I)について.
 の異なる二つの1次元部分空間を
の異なる二つの1次元部分空間を
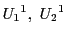 とし,
その基底をそれぞれ
とし,
その基底をそれぞれ
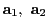 ,つまり
,つまり
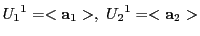 とする.
このとき,
とする.
このとき,
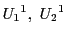 を含む2次元部分空間
を含む2次元部分空間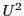 が
が
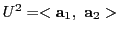 で定まり,この他にない.よって公理I)が成りたつ.
で定まり,この他にない.よって公理I)が成りたつ.
公理II)について.
異なる1次元部分空間
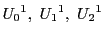 が同一の2次元部分空間上にあり,
それらとは異なる
が同一の2次元部分空間上にあり,
それらとは異なる
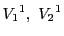 について,
異なる1次元部分空間
について,
異なる1次元部分空間
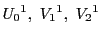 が同一の2次元部分空間上にあるとする.
が同一の2次元部分空間上にあるとする.
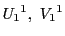 を含む2次元部分空間を
を含む2次元部分空間を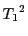 ,
,
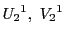 を含む2次元部分空間を
を含む2次元部分空間を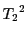 とする.
このとき,
とする.
このとき,
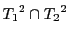 の次元が1以上であることを示せばよい.
の次元が1以上であることを示せばよい.
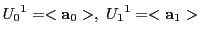 とすると,
とすると,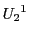 が
が
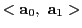 上にあるので,
上にあるので,
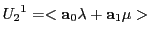 となる
となる
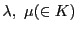 がある.
同様に
がある.
同様に
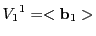 とする.
とする.
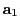 と
と
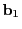 は一次独立である.
は一次独立である.
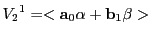 となる
となる
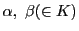 がある.
がある.
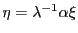 にとると
にとると
となる.これは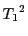 にも含まれる.つまり
にも含まれる.つまり
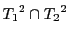 には
には
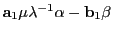 を基底とする1次元部分空間が含まれている.
を基底とする1次元部分空間が含まれている.
公理III)について.
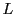 の要素
の要素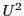 をとる.
をとる.
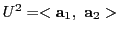 とする.
このとき,
とする.
このとき,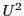 上には,
上には,
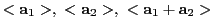 の少なくとも3つの1次元部分空間が含まれている.
の少なくとも3つの1次元部分空間が含まれている.
公理I)〜III)をもとに の部分空間が定義される.
明らかに射影空間
の部分空間が定義される.
明らかに射影空間 の部分空間は,
の部分空間は,
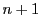 次元線形空間
次元線形空間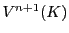 の部分空間と対応する.
の部分空間と対応する.
公理IV)について.
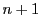 次元線形空間
次元線形空間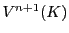 の基底を
の基底を
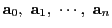 とする.
このとき
とする.
このとき の要素
の要素
を含む部分空間が と一致する.よって公理IV)が成立する.
□
と一致する.よって公理IV)が成立する.
□
とする.これは,順次上に素な部分空間の列であり, は
は 次元射影空間である.
次元射影空間である.
このようにして構成された の点とは,
の点とは,
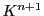 の1次元部分空間,つまり原点を通る直線である.
それは方向ベクトルと一対一に対応し,
の1次元部分空間,つまり原点を通る直線である.
それは方向ベクトルと一対一に対応し,
 はこのような方向ベクトルの集合と同一視される.
はこのような方向ベクトルの集合と同一視される.
上記モデルにおいて
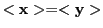 であることは
であることは
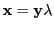 となる0でない
となる0でない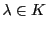 が存在することと同値である.
が存在することと同値である.
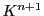 から
から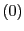 を除いた
を除いた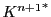 における関係
における関係
は同値関係である.
この同値関係による商集合を とする.
つまり
とする.
つまり
とする.そして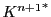 の要素
の要素
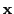 が代表する
が代表する
 の要素を
の要素を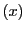 と表し,これを同次座標という.
と表し,これを同次座標という.
同次座標を用いて命題31を書き直せば次のようになる.
命題 32

の要素
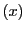
と
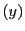
に対して,
とし,
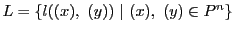
とする.
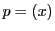
と点,
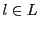
を直線と呼び,
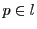
のとき
直線

は点

を通るとすれば,
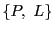
は射影幾何の公理I)〜IV)を満たす.
■
こうして一つのモデルを構成することが出来た.
このモデルの同次座標による表現を射影幾何の解析的表示という.
また,『射影幾何学』[35]の31頁にあるように,
モデルの存在が,数体の無矛盾性を根拠として,
公理系I)〜IV)が互いに矛盾しないことを示している.


 次: 射影写像
上: 射影幾何の公理
前: 公理系を立てる
2014-01-03
次: 射影写像
上: 射影幾何の公理
前: 公理系を立てる
2014-01-03
![]() を考え,
を考え,![]() や
や![]() で
で![]() の要素を表す.
集合
の要素を表す.
集合![]() が次の条件を満たすとき,体という.
が次の条件を満たすとき,体という.
![]() が成り立つものを可換体と呼ぶ.
が成り立つものを可換体と呼ぶ.
![]() を体とし,
を体とし,![]() を
を![]() の0でない要素とする.
の0でない要素とする.![]() から
から![]() への写像で
への写像で
![]() が可換体なら内部自己同型は恒等写像のみである.
実数体や複素数体はもとより可換体であり,
内部自己同型群
が可換体なら内部自己同型は恒等写像のみである.
実数体や複素数体はもとより可換体であり,
内部自己同型群![]() は恒等写像のみの群である.
は恒等写像のみの群である.
![]() なので,
なので,
![]() と整数
と整数![]() と
と![]() で表す.
正整数
で表す.
正整数![]() に関しては,
に関しては,
![]() が体の同型であることから
が体の同型であることから
![]() なので
なので![]() はある0でない実数
はある0でない実数![]() を用いて
を用いて![]() と表される.
よって
と表される.
よって
![]() の部分集合
の部分集合![]() で,
で,
![]() の右からの積で閉じており,それ自身同様に
の右からの積で閉じており,それ自身同様に![]() 右加群であり,
かつ
右加群であり,
かつ![]() 個よりなる基底が存在するものを
個よりなる基底が存在するものを![]() 次元部分空間という.
■
次元部分空間という.
■
![]() 上の
上の![]() 次元右線形空間の要素を
次元右線形空間の要素を
![]() のように添え数を0からはじめるものとする.
のように添え数を0からはじめるものとする.
![]() の異なる二つの1次元部分空間を
の異なる二つの1次元部分空間を
![]() とし,
その基底をそれぞれ
とし,
その基底をそれぞれ
![]() ,つまり
,つまり
![]() とする.
このとき,
とする.
このとき,
![]() を含む2次元部分空間
を含む2次元部分空間![]() が
が
![]() で定まり,この他にない.よって公理I)が成りたつ.
で定まり,この他にない.よって公理I)が成りたつ.
![]() が同一の2次元部分空間上にあり,
それらとは異なる
が同一の2次元部分空間上にあり,
それらとは異なる
![]() について,
異なる1次元部分空間
について,
異なる1次元部分空間
![]() が同一の2次元部分空間上にあるとする.
が同一の2次元部分空間上にあるとする.
![]() を含む2次元部分空間を
を含む2次元部分空間を![]() ,
,
![]() を含む2次元部分空間を
を含む2次元部分空間を![]() とする.
このとき,
とする.
このとき,
![]() の次元が1以上であることを示せばよい.
の次元が1以上であることを示せばよい.
![]() とすると,
とすると,![]() が
が
![]() 上にあるので,
上にあるので,
![]() となる
となる
![]() がある.
同様に
がある.
同様に
![]() とする.
とする.
![]() と
と
![]() は一次独立である.
は一次独立である.
![]() となる
となる
![]() がある.
がある.
![]() の要素
の要素![]() をとる.
をとる.
![]() とする.
このとき,
とする.
このとき,![]() 上には,
上には,
![]() の少なくとも3つの1次元部分空間が含まれている.
の少なくとも3つの1次元部分空間が含まれている.
![]() の部分空間が定義される.
明らかに射影空間
の部分空間が定義される.
明らかに射影空間![]() の部分空間は,
の部分空間は,
![]() 次元線形空間
次元線形空間![]() の部分空間と対応する.
の部分空間と対応する.
![]() 次元線形空間
次元線形空間![]() の基底を
の基底を
![]() とする.
このとき
とする.
このとき![]() の要素
の要素