

 次: 諸定義とその関係
上: 二次曲面の定義
前: 二次曲面の定義
次: 諸定義とその関係
上: 二次曲面の定義
前: 二次曲面の定義
われわれは射影幾何の公理からはじめて,直線体と係数体を定義し,
それによる座標の導入と射影写像の座標表現まですすんだ.
また古典的な複比を射影幾何の公理系のもとで再定義した.
これらをもとに二次曲面を定義する.これは基本的に線型代数の範疇である.
その後,古典的で幾何的な二次曲面の定義をおこなう.
2次元射影空間(射影平面ともいう)の場合にそれらの定義の同等性を確認し,
その下で射影平面上の二次曲面としての円錐曲線の古典的な諸性質を証明する.
前章最終節の複比を考える段階で直線体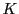 は可換であるとした.以下においても係数体
は可換であるとした.以下においても係数体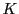 は可換体であるとする.
は可換体であるとする.
射影幾何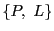 の双対射影幾何を
の双対射影幾何を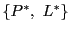 とする.
とする.
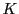 が可換であるので,
命題56によってその双対空間
が可換であるので,
命題56によってその双対空間 の係数体は
の係数体は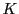 と同型である.
と同型である.
 のモデルを
のモデルを の同次座標から構成しよう.
の同次座標から構成しよう.
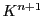 から
から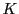 への線型写像
への線型写像 をとる.
線型写像とは次の条件を満たす写像である.
をとる.
線型写像とは次の条件を満たす写像である.
二つの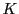 への線型写像
への線型写像
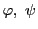 に対して
その一次結合
に対して
その一次結合
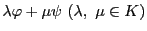 を
を
によって定める.
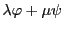 がまた
がまた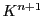 から
から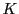 への線形写像であることはただちに確認できる.
これによって
への線形写像であることはただちに確認できる.
これによって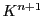 から
から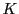 への線型写像の集合はそれ自身
への線型写像の集合はそれ自身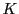 上のベクトル空間となる.
上のベクトル空間となる.
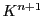 から
から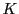 への線型写像の集合を
への線型写像の集合を
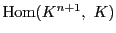 と表す.
と表す.
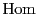 は一般に準同型写像(homomorphism)を意味する.
ベクトル空間
は一般に準同型写像(homomorphism)を意味する.
ベクトル空間
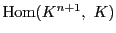 を
を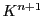 の双対ベクトル空間という.
の双対ベクトル空間という.
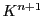 の基底
の基底
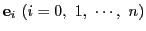 に対し
に対し
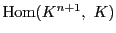 の要素
の要素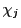 を,線型写像でありかつ
を,線型写像でありかつ
となるものとして定める.
これら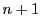 個の
個の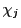 は
ベクトル空間
は
ベクトル空間
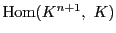 の基底となり,
この結果
の基底となり,
この結果
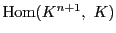 のベクトル空間としての次元が
のベクトル空間としての次元が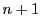 であることもわかる.この基底を標準基底という.
であることもわかる.この基底を標準基底という.
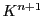 の要素
の要素
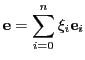 と
と
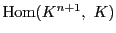 の要素
の要素
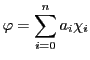 に対して
に対して
となる.
ベクトル空間
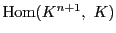 から0ベクトルを除き,
その集合の定数倍という同値関係での商集合
から0ベクトルを除き,
その集合の定数倍という同値関係での商集合
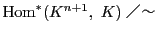 はやはり射影空間である.
はやはり射影空間である.
命題 74
射影空間
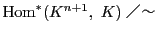
と
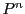
の双対射影空間

は射影幾何として同型である.
■
証明
0でない
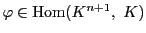 に対して
に対して
と定めると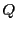 はそれ自身ベクトル空間
はそれ自身ベクトル空間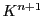 の部分ベクトル空間である.
の部分ベクトル空間である.
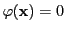 であれば
であれば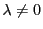 に対して
に対して
となるので,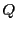 は
は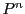 の超平面を定める.超平面は双対射影空間
の超平面を定める.超平面は双対射影空間 の点
の点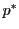 を定める.
を定める.
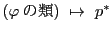 によって
によって
の写像が定まる.
逆に, の超平面
の超平面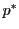 は命題55によって
は命題55によって
と表せる.ただし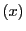 は
は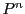 の同次座標,
の同次座標,
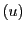 は
は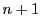 組の
組の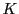 の要素である.
の要素である.
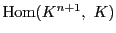 の要素
の要素 を
を
で定めると,これによって
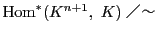 における
における
 の類が一意に定まる.
つまり
の類が一意に定まる.
つまり
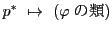 によって
によって
の写像が定まる.
これが互いに逆の対応であり,射影空間の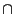 と
と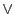 を保つことは,
線型代数の基礎のうえに示される.
その確認は略する.
この結果,射影幾何の同型が確定した.
□
を保つことは,
線型代数の基礎のうえに示される.
その確認は略する.
この結果,射影幾何の同型が確定した.
□
今後この同型によって
 と
と
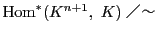 を同一視する.
を同一視する.
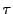 を
を から
から への共線写像とする.
このとき次のようにして
への共線写像とする.
このとき次のようにして から
から への共線写像が定まる.
これを
への共線写像が定まる.
これを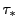 で表す.
で表す.
 の点
の点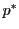 は
は の超平面である.
共線写像は超平面を超平面にうつす.
よって
の超平面である.
共線写像は超平面を超平面にうつす.
よって の超平面
の超平面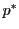 に対し
に対し
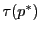 は
は の超平面である,
の超平面である,
 の超平面は
の超平面は の点
の点 を定める.
これを
を定める.
これを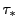 による
による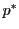 の像とする.
つまり
の像とする.
つまり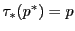 によって
によって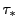 を定める.
を定める.
これが共線写像であることは定義から明らかである.
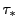 を,
を,
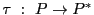 が誘導する
が誘導する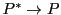 の共線写像,という.
射影空間
の共線写像,という.
射影空間 からその双対空間
からその双対空間 への射影写像
への射影写像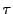 を
射影相反変換という.
係数体が実数体であれば共線写像は射影写像であるので射影相反変換と相反変換に違いはない.
恒等写像ではない自己同型をもつ体,例えば複素数体ではこれは同じではない.
を
射影相反変換という.
係数体が実数体であれば共線写像は射影写像であるので射影相反変換と相反変換に違いはない.
恒等写像ではない自己同型をもつ体,例えば複素数体ではこれは同じではない.
 や
や の座標ベクトルは縦ベクトルとする.
これに注意して,
の座標ベクトルは縦ベクトルとする.
これに注意して,
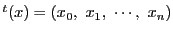 とする.
また
とする.
また の座標系として同型な
の座標系として同型な
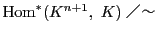 の座標系
の座標系
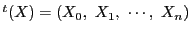 を用いる.
を用いる.
このとき,射影相反変換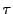 はそれぞれの座標系の成分を用いて
はそれぞれの座標系の成分を用いて
と表現される.この行列を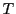 とする.これは
簡略して
とする.これは
簡略して
と表すことができる.
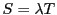 となる
となる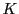 の数
の数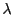 が存在するとき,
が存在するとき,
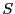 と
と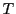 は同じ変換を表す.
は同じ変換を表す.
以下,変換に対応する行列は,
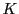 上の
上の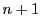 次行列で逆行列をもつものを
次行列で逆行列をもつものを
で類別したものであり,その類の代表を表している、とする.
また座標系もそれぞれ類を表していることに注意しよう.
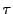 の誘導する
の誘導する
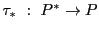 の射影相反写像を具体的に書き表そう.
今
の射影相反写像を具体的に書き表そう.
今 の点
の点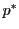 をとる.この超平面座標を
をとる.この超平面座標を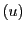 とする.
また上記同型によって点
とする.
また上記同型によって点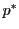 が対応する
が対応する
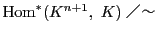 の座標を
の座標を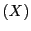 とする.
とする.
 と
と
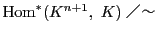 の同型によって,
の同型によって,
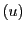 と
と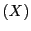 とを同一視する.
とを同一視する.
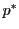 は
は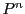 の超平面
の超平面
となる.
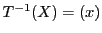 なので,
なので,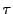 によってこの超平面は
によってこの超平面は
にうつる.これは の超平面であり,
の超平面であり, の点を定める.
の点を定める.
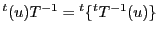 なので,
これは
なので,
これは
と書ける.よって定められる の点は
の点は
である.つまり の点
の点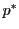 である超平面,
それを超平面座標で表すと
である超平面,
それを超平面座標で表すと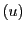 であるが,この点は
であるが,この点は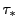 によって
によって
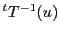 にうつる.
にうつる.
 から
から への射影相反変換
への射影相反変換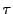 と,
それが誘導する
と,
それが誘導する から
から への射影相反変換
への射影相反変換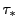 を合成した
を合成した
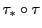 は
は の射影変換になる.
これが恒等写像であるとき
の射影変換になる.
これが恒等写像であるとき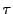 を対合的射影相反変換という.
を対合的射影相反変換という.
と
を合成すれば
これが恒等写像ということは単位行列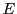 と同じ類に属するということであり,
と同じ類に属するということであり,
となる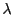 が存在する.これは成分で書けば
が存在する.これは成分で書けば
なので,
がすべての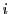 と
と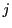 で成り立つ.これから
で成り立つ.これから
である.成分には0でないものがあるので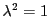 つまり
つまり
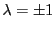 である.
である.
定義 28
対合的射影相反変換のうち,
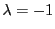
,つまり
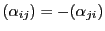
であるものを
零系という.
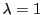
,つまり
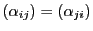
であるものを
極系という.
■


 次: 諸定義とその関係
上: 二次曲面の定義
前: 二次曲面の定義
2014-01-03
次: 諸定義とその関係
上: 二次曲面の定義
前: 二次曲面の定義
2014-01-03
![]() は可換であるとした.以下においても係数体
は可換であるとした.以下においても係数体![]() は可換体であるとする.
は可換体であるとする.
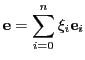 と
と
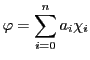 に対して
に対して
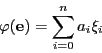
![]() の超平面
の超平面![]() は命題55によって
は命題55によって
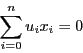
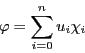
![]() と
と![]() を保つことは,
線型代数の基礎のうえに示される.
その確認は略する.
この結果,射影幾何の同型が確定した.
□
を保つことは,
線型代数の基礎のうえに示される.
その確認は略する.
この結果,射影幾何の同型が確定した.
□
![]() と
と
![]() を同一視する.
を同一視する.
の点
は
の超平面である. 共線写像は超平面を超平面にうつす. よって
の超平面
に対し
は
の超平面である,
の超平面は
の点
を定める. これを
による
の像とする. つまり
によって
を定める.
![]() や
や![]() の座標ベクトルは縦ベクトルとする.
これに注意して,
の座標ベクトルは縦ベクトルとする.
これに注意して,
![]() とする.
また
とする.
また![]() の座標系として同型な
の座標系として同型な
![]() の座標系
の座標系
![]() を用いる.
を用いる.
![]() はそれぞれの座標系の成分を用いて
はそれぞれの座標系の成分を用いて
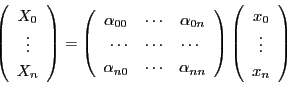
![]() となる
となる![]() の数
の数![]() が存在するとき,
が存在するとき,
![]() と
と![]() は同じ変換を表す.
は同じ変換を表す.
![]() 上の
上の![]() 次行列で逆行列をもつものを
次行列で逆行列をもつものを
![]() の誘導する
の誘導する
![]() の射影相反写像を具体的に書き表そう.
今
の射影相反写像を具体的に書き表そう.
今![]() の点
の点![]() をとる.この超平面座標を
をとる.この超平面座標を![]() とする.
また上記同型によって点
とする.
また上記同型によって点![]() が対応する
が対応する
![]() の座標を
の座標を![]() とする.
とする.
![]() と
と
![]() の同型によって,
の同型によって,
![]() と
と![]() とを同一視する.
とを同一視する.
![]() は
は![]() の超平面
の超平面