![]() 次元射影空間
次元射影空間![]() の直線
の直線![]() とその上の枠
とその上の枠
![]() がある.
このとき
がある.
このとき![]() の直線体
の直線体
![]() が定まる.
これは直線
が定まる.
これは直線![]() の点から
の点から![]() を除いた点の集合に体の構造を入れたものである.
この体は命題45により,
枠
を除いた点の集合に体の構造を入れたものである.
この体は命題45により,
枠
![]() のとり方によらず同型である.
つまりひとつの抽象体としての係数体
のとり方によらず同型である.
つまりひとつの抽象体としての係数体![]() が定まる.
が定まる.
![]() を同型写像
を同型写像
![]() とする.
とする.
![]() は集合としては
直線
は集合としては
直線![]() の点から
の点から![]() を除いたものである.
よって
を除いたものである.
よって![]() は
は
![]() の点
の点![]() を除いた点集合と
を除いた点集合と![]() の一対一対応を定める.
この対応も同じ
の一対一対応を定める.
この対応も同じ![]() で表す.
で表す.
![]() を直線
を直線![]() の座標系,
の座標系,
![]() でない
でない![]() の要素
の要素![]() に対応する
に対応する![]() の要素
の要素![]() を
点
を
点![]() のこの枠に対する非同次座標という.
のこの枠に対する非同次座標という.
それに対して
![]() となる
となる
![]() の要素の組
の要素の組![]() を
を![]() の同次座標という.
の同次座標という.
![]() がともに0でないとき直線
がともに0でないとき直線![]() 上の点
上の点![]() が
が![]() に,
点
に,
点![]() が
が![]() に対応するとすれば,
に対応するとすれば,
![]() と
と![]() は体
は体
![]() の要素として,
の要素として,
![]() を満たす.
一方,ただちに確認できるように,
命題46の写像
を満たす.
一方,ただちに確認できるように,
命題46の写像![]() で
で![]() には
には![]() が,
が,
![]() には
には![]() が対応する.
よって
が対応する.
よって![]() の点
の点![]() に対しては同次座標
に対しては同次座標![]() を対応させると定めることは自然であり,
これによって
を対応させると定めることは自然であり,
これによって![]() 上のすべての点に対して,その同次座標が定まる.
2つの組
上のすべての点に対して,その同次座標が定まる.
2つの組
![]() が同じ点の同次座標であるための必要十分条件は,
が同じ点の同次座標であるための必要十分条件は,
![]() ,
,
![]() となる0でない
となる0でない![]() の要素
の要素![]() が存在することである.
が存在することである.
体![]() の要素を成分とする2次元ベクトル空間を
の要素を成分とする2次元ベクトル空間を![]() とする.
とする.
![]() から
から![]() を除いた集合を
を除いた集合を![]() と表す.
と表す.
![]() の要素の間に同値関係〜を
の要素の間に同値関係〜を
一次変換を非同次座標で表す.![]() のとき
のとき
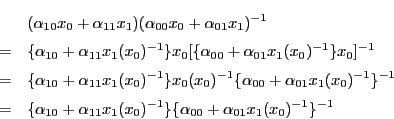
逆に非同次座標で![]() を除く
を除く![]() の点
の点![]() に対する
に対する![]() に対し
に対し
![]() が可換体の場合は,いわゆる一次分数変換である.
が可換体の場合は,いわゆる一次分数変換である.
証明 一対一の一次変換
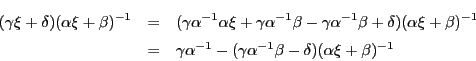
逆に![]() から
から![]() への射影写像
への射影写像![]() をとる.
をとる.
![]() の
の
![]() は
同次座標で
は
同次座標で
![]() で表される.
で表される.
![]() によるこれらの像を
によるこれらの像を
![]() ,
,
![]() ,
,
![]() とする.
とする.
![]() 上の相異なる3点である.
これに対して,一次変換
上の相異なる3点である.
これに対して,一次変換
さらに
![]() または
または![]() のとき.
のとき.
![]() なら,
なら,![]() ,
,![]() は異なる点なので
は異なる点なので
![]() ということはない.よって
ということはない.よって
![]() となるように
となるように![]() と
と![]() をとることができ,
このとき
をとることができ,
このとき![]() が存在する.
が存在する.![]() のときも同様である.
のときも同様である.
次に![]() かつ
かつ![]() のとき.
この条件は
のとき.
この条件は
![]() と
と![]() はともに同じ3点を同じ3点に移す射影変換である,
定理6と注意3.2.5から非同次座標で表せば
はともに同じ3点を同じ3点に移す射影変換である,
定理6と注意3.2.5から非同次座標で表せば![]() の内部自己同型
の内部自己同型
![]() しか違わない.これ自身一次変換であるのでこれを
しか違わない.これ自身一次変換であるのでこれを![]() に結合してもやはり
に結合してもやはり
![]() は一次変換である.□
は一次変換である.□
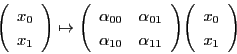
![]() と
と
![]() に対応する射影変換が
等しいことはある
に対応する射影変換が
等しいことはある![]() の要素
の要素![]() があって
があって
一般の枠では,
直線![]() 上の直線体を定めるのに
上の直線体を定めるのに![]() のいずれを原点,示点にとる
こともできる.それでこのように枠の点を原点,示点の区別のない形でとる.
のいずれを原点,示点にとる
こともできる.それでこのように枠の点を原点,示点の区別のない形でとる.
辺![]() 上には枠
上には枠
![]() ,
,
![]() が定まり,
直線体
が定まり,
直線体![]() や
や![]() が定まる.
が定まる.
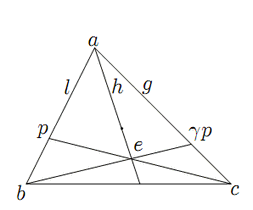 枠
枠1点![]() に対して
に対して![]() を通る2辺
を通る2辺![]() ,
,![]() の間の射影写像
の間の射影写像
![]() を
を
定義から逆写像![]() も折返しである.
これらは配景写像の合成で射影写像であり,
折返しおよびそれらの合成写像も枠から枠への射影写像である.
も折返しである.
これらは配景写像の合成で射影写像であり,
折返しおよびそれらの合成写像も枠から枠への射影写像である.
定義 22 (基本写像)
![]() の枠
の枠
![]() をとる.
2辺のあいだの写像
をとる.
2辺のあいだの写像
![]() であって,
枠
であって,
枠![]() の2次元面上の折返しを有限回結合して得られるものを
枠
の2次元面上の折返しを有限回結合して得られるものを
枠![]() に関する基本写像という.
■
に関する基本写像という.
■
証明 単位点のそれぞれの辺上の成分を
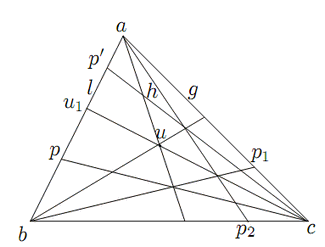
![]() とする.
とする.
![]() ,
,
![]() とおく.
6直線
とおく.
6直線
![]() は
4直線
は
4直線
![]() ,
,
![]() ,
,
![]() ,
,
![]() でつくられる四辺形によって四辺性六辺である.
したがって命題42によって
6点
でつくられる四辺形によって四辺性六辺である.
したがって命題42によって
6点
![]() は四角性六点.
直線体の積の定義から
は四角性六点.
直線体の積の定義から![]() である.
□
である.
□
証明
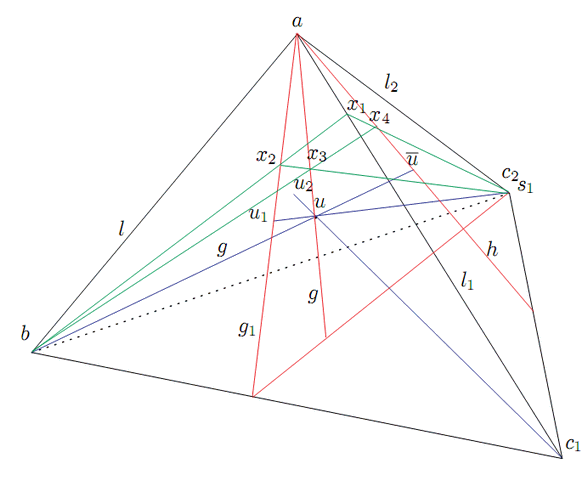
命題51の証明
![]() の枠
の枠
![]() に属する任意の辺上の枠
に属する任意の辺上の枠
![]() に対して基本写像
に対して基本写像
1)
![]() のとき.
のとき.
2辺
![]() を含む
を含む![]() の2次元面
の2次元面![]() をとり,
をとり,
![]() 上の枠に関する基本写像を
上の枠に関する基本写像を![]() とする.
とする.
![]() のときの一意性から
のときの一意性から![]() は一意に定まる.
は一意に定まる.
2)
![]() のとき.
のとき.
枠
![]() と枠
と枠
![]() に関する折返しの結合により
に関する折返しの結合により![]() を
を
![]() の枠
の枠
![]() が与えられている.
その係数体を
が与えられている.
その係数体を![]() とし,直線体
とし,直線体
![]() または
または
![]() から
から![]() への同型
への同型![]() が指定されている.
このとき,写像
が指定されている.
このとき,写像
![]() が
が![]() に関する基本写像であるとき
に関する基本写像であるとき![]() と写像
と写像![]() の組
の組
![]() を
を![]() の非同次射影座標系という.
の非同次射影座標系という.
命題51により,いずれかの![]() を決めれば他は一意に定まる.
よって
を決めれば他は一意に定まる.
よって![]() をすべて同じ
をすべて同じ![]() で表して混乱しない.
座標系を
で表して混乱しない.
座標系を
![]() のように表す.
のように表す.
![]() の決め方は二通りあり,その結果,枠
の決め方は二通りあり,その結果,枠![]() に対して二通りの非同次座標系が定まる.
に対して二通りの非同次座標系が定まる.
証明
![]() が共線なら
が共線なら
![]() なので
なので
![]() より成立.
より成立.
![]() が共線なら
が共線なら
![]() なので命題50
より
なので命題50
より
![]() かつ
かつ![]() より成立.
より成立.
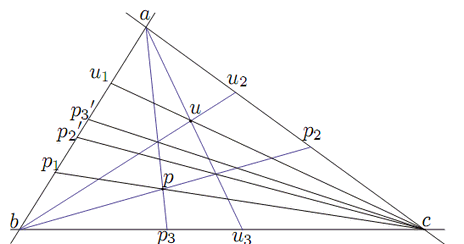 その他の一般の場合,
その他の一般の場合,
![]() ,
,
![]() とおくと,同型
とおくと,同型
![]() に関して
に関して
![]()
である.4直線![]() ,
,![]() ,
,![]() ,
,![]() で定まる四辺形に関して
6直線
で定まる四辺形に関して
6直線
![]()
は四辺性六辺である.
この結果,6点
![]() は四角性六点である.
よって積の定義から体
は四角性六点である.
よって積の定義から体
![]() において
において
![]() .つまり
.つまり![]() において
において
![]() が成り立つ.
□
が成り立つ.
□
同次座標を定義するために,座標集合を準備する.
体![]() の
の![]() 個の要素の組
個の要素の組
![]() から
から
![]() を除いた
を除いた![]() の,
同値関係
の,
同値関係
![]() に射影座標系
に射影座標系
![]() ,
,
![]() が与えられている.
が与えられている.
点![]() が
が![]() の補面
の補面![]() に含まれないとき,
に含まれないとき,![]() の辺
の辺
![]() への成分を
への成分を![]() とし,
とし,
![]() による
による![]() の像を,
の像を,
![]() とする.そして
とする.そして
![]() を点
を点![]() の非同次座標という.またこのとき
の非同次座標という.またこのとき
![]() を点
を点![]() の同次座標という.点
の同次座標という.点![]() の同次座標は
の同次座標は
![]() である.
である.
さらに![]() のときは,直線
のときは,直線![]() 上の第3の点
上の第3の点![]() をとり,
をとり,
![]() の非同次座標が
の非同次座標が
![]() であるとき,
であるとき,
![]() を点
を点![]() の同次座標と定める.
の同次座標と定める.
この定義が意味をもつためには,![]() のとり方を変えても,
のとり方を変えても,
![]() が
が
![]() の要素として
同じ類となることを確認しなければならない.それを示す.
の要素として
同じ類となることを確認しなければならない.それを示す.
 直線
直線![]() 上の点
上の点
![]() をとる.
その非同次座標を
をとる.
その非同次座標を
![]() ,
,
![]() とする.
とする.
![]() なので,
なので,
![]() のすべてが0ということはない.
順序を入れかえ
のすべてが0ということはない.
順序を入れかえ![]() とする.このとき
とする.このとき![]() も成り立つ.
も成り立つ.
![]() の中で0でないものがなければ,一意性は明らか.0でないものがあればそれを
の中で0でないものがなければ,一意性は明らか.0でないものがあればそれを![]() とする.
3点
とする.
3点![]() の面
の面
![]() への成分を
それぞれ
への成分を
それぞれ
![]() とする.
4点
とする.
4点
![]() は共線で,
は共線で,
![]() より
より
![]() .
.
面上の枠
![]() に関する点
に関する点![]() の非同次座標が
の非同次座標が
![]() ,
,
![]() である.
ここで
である.
ここで![]() から
から![]() への同型写像
への同型写像![]() をとり,
をとり,
![]() とおくと,命題52から
とおくと,命題52から
![]() となる.
となる.
この結果,
![]() .
これから
.
これから
![]() .
この値を
.
この値を![]() とおけば
とおけば
![]() で
で
![]() が
が
![]() で成立.
つまり
で成立.
つまり
![]() と
と
![]() は
は
![]() の同じ類を表す.
の同じ類を表す.
これで射影空間![]() の同次座標が定義された.
これを枠
の同次座標が定義された.
これを枠![]() によって定まる同次座標系といい,
同じ記号
によって定まる同次座標系といい,
同じ記号
![]() で表す.
で表す.
直線![]() が枠の辺と一致するとき.
同次座標の定義から3辺
が枠の辺と一致するとき.
同次座標の定義から3辺
![]() の方程式はそれぞれ
の方程式はそれぞれ
直線![]() が頂点
が頂点![]() を通り
を通り![]() を通らないとき.
を通らないとき.
![]() ,
,
![]() ,
,![]() 上の点の非同次座標を
上の点の非同次座標を
![]() とすれば,命題52から
とすれば,命題52から
![]() であるから,
であるから,![]() の方程式は同次座標で
の方程式は同次座標で
![]() となる.他も同様で
となる.他も同様で![]() が
が![]() の一つの頂点を通るとき,その方程式は
の一つの頂点を通るとき,その方程式は
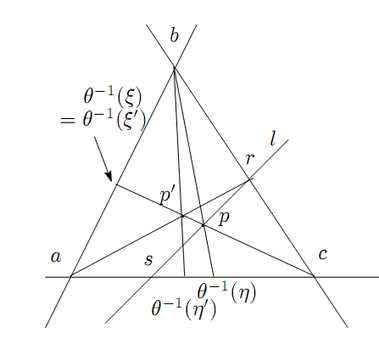 直線
直線![]() が
が![]() のいずれの頂点も通らないとき.
のいずれの頂点も通らないとき.
![]() と辺の交点
と辺の交点
![]() ,
,
![]() をとる.
をとる.
![]() に対して
に対して
![]() とする.
とする.
![]() 上の点
上の点![]() と
と
![]() をとり,それらの枠
をとり,それらの枠
![]() に関する
非同次座標を
に関する
非同次座標を
![]() とする.
命題52から
とする.
命題52から![]() ,
,![]() である.
である.
4点
![]() を頂点とする四角形から,体
を頂点とする四角形から,体![]() の和の定義より
の和の定義より
![]() ,これから
,これから![]() である.同次座標になおして
である.同次座標になおして
![]() の方程式は
の方程式は
逆に方程式(3.1)は以上のいずれかの形に変形でき, 直線を表す. □
命題 54
![]() に射影座標系が定まっている.
相異なる2定点
に射影座標系が定まっている.
相異なる2定点![]() を通る直線
を通る直線![]() は,
媒介変数
は,
媒介変数
![]() を用いて
を用いて
証明
![]() 上の点が等式(3.2)の形に表されることを数学的帰納法で示す.
上の点が等式(3.2)の形に表されることを数学的帰納法で示す.
1)
![]() のとき.
のとき.
![]() は命題53の直線の方程式を満たす.
は命題53の直線の方程式を満たす.
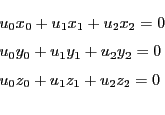
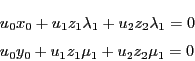
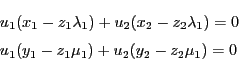
![]() のとき.
のとき.
![]() とする.上記証明ですべて
とする.上記証明ですべて![]() とおいてそのまま成り立つ.
とおいてそのまま成り立つ.
![]() のとき.このとき直線の方程式は
のとき.このとき直線の方程式は![]() となり,
点の同次座標は
となり,
点の同次座標は
![]() である.
である.
![]() とする.
とする.![]() より
より
![]() なので,
なので,
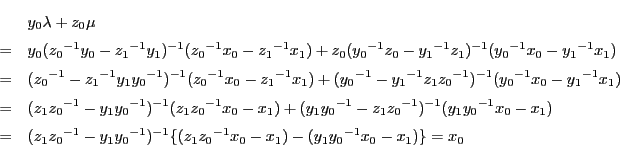
2)
![]() では成立とする.
では成立とする.
![]() のとき.枠を
のとき.枠を
![]() とする.
必要なら基本点の順を替え,
とする.
必要なら基本点の順を替え,![]() と
と![]() を通る直線
を通る直線![]() は
辺
は
辺![]() と交わらないとする.
と交わらないとする.
![]() 上の点
上の点![]() をとり,3点の補面
をとり,3点の補面![]() への成分,
および補面
への成分,
および補面![]() への成分もまたそれぞれ共線であり,
補面は
への成分もまたそれぞれ共線であり,
補面は![]() 次元なので,仮定から
次元なので,仮定から
逆に等式(3.2)の形に表される点
![]() は
は
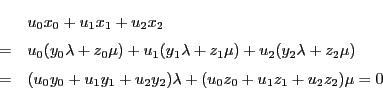
われわれは,命題31において任意の体![]() 上の射影空間の存在を示した.
上の射影空間の存在を示した.
それをもとに,命題32で射影幾何の同次座標による解析的表示を得た. 命題32で直線の表示を構成したが, 本命題によって,直線はつねにこの形に表示される. よって,射影空間の構成ということに関して, 命題31のモデル以外のモデルは存在しない.
証明 一般に
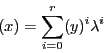
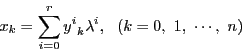
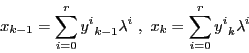
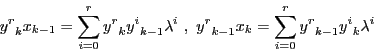
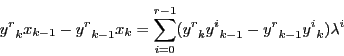
![]() の超平面とは,
の超平面とは,![]() 次元の部分空間であった.
次元の部分空間であった.
![]() の場合,係数を左から揃えて媒介変数を減じる操作を
の場合,係数を左から揃えて媒介変数を減じる操作を![]() 回行うことで,
関係式は1個になる.
よって超平面は1個の1次方程式で表される.
□
回行うことで,
関係式は1個になる.
よって超平面は1個の1次方程式で表される.
□
超平面は
![]() の類
の類
![]() で一意に確定する.
これを超平面座標という.
で一意に確定する.
これを超平面座標という.
![]() と
と![]() を二つの超平面とし,
その超平面座標を
を二つの超平面とし,
その超平面座標を![]() ,
,![]() とするとき,
とするとき,
![]() 次元部分空間
次元部分空間
![]() を含む超平面は,
を含む超平面は,
![]() と
と
![]() と
の共有点を含む超平面であるから,
と
の共有点を含む超平面であるから,
ここで体![]() に対して逆体
に対して逆体![]() を
集合としては
を
集合としては![]() と同じであり,和も同様であるが,
と同じであり,和も同様であるが,
![]() の積
の積![]() に対して積
に対して積![]() が
が
![]() 次元座標空間から
次元座標空間から![]() を構成した命題31の構成法にならい,
を構成した命題31の構成法にならい,
![]() 次元の座標である超平面座標を用いて
次元の座標である超平面座標を用いて![]() を構成することができる.
ただし,上記の超平面座標の係数
を構成することができる.
ただし,上記の超平面座標の係数![]() が左からかかっていることから,
が左からかかっていることから,
![]() の逆体
の逆体![]() を用意し,
これを用いて命題31と同様の構成を行うと,
を用意し,
これを用いて命題31と同様の構成を行うと,
![]() が
が
以上より次のことがわかる.
この結果,例えば次のような命題もまた成立する.
射影幾何の公理を満たすさまざまのモデルが構成できる. 射影幾何の公理系の外部で体の内部構造は定まる. したがって,その体が可換であるとか,内部自己同型をもつかどうかなどは, 射影幾何の公理そのものからは出ない.
いいかえると,公理から出発したわれわれの方法は, さまざまの体上の射影幾何のモデルに共通なことを公理に抽出し, そこから逆に射影幾何を構成することで, 体の独自性によらない共通の構造はどこまで成り立つのか, 探求してきたことになる.
一方,命題31によって,
体![]() が与えられたとき,
ベクトル空間
が与えられたとき,
ベクトル空間![]() をもとに定義された直線の集合と平面の集合の組
をもとに定義された直線の集合と平面の集合の組![]() は射影幾何であることが証明された.
逆にそこから,この射影幾何の係数体をこれまでの論法で定義したとき,
それがもとの体
は射影幾何であることが証明された.
逆にそこから,この射影幾何の係数体をこれまでの論法で定義したとき,
それがもとの体![]() と同型であることを,確認しなければならない.
と同型であることを,確認しなければならない.
証明
そこで![]() の同時座標系を
の同時座標系を
![]() として,
4点
として,
4点
![]() と
と
![]() になっていることが確認されれば,
になっていることが確認されれば,
![]() が体
が体![]() と体
と体
![]() の同型を導くものであることが示される.
の同型を導くものであることが示される.
和と積の定義21の図をもとにこれを確認する.
ただし,体![]() の和積と直線体の演算の区別を明確にするため
点
の和積と直線体の演算の区別を明確にするため
点
![]() などを
などを![]() のようにおく.
のようにおく.
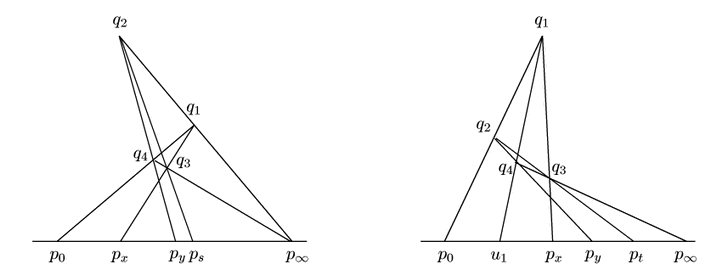
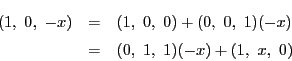
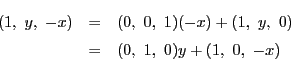
積 積についても次の順に点を決めてゆく.
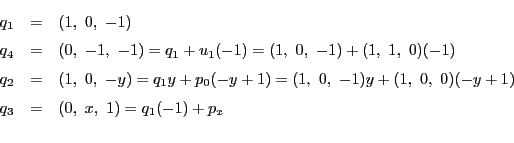
演算を保存する体の一対一対応は体の同型に他ならない.
これで体![]() と直線体
と直線体
![]() が同型となり,
直線体
が同型となり,
直線体
![]() と同型な抽象体として定まる係数体と体
と同型な抽象体として定まる係数体と体![]() は同型である.
は同型である.
□
以上の議論によって次のことが示された.
を満たすとき,の3点
が共線であるとき,そしてそのときにかぎり,それらの像
も共線である.
射影空間は射影幾何の公理を満たす点の集合![]() と直線の集合
と直線の集合![]() の組
の組![]() であった.
共線写像
であった.
共線写像![]() は,
二つの射影空間
は,
二つの射影空間![]() と
と![]() において,
において,![]() と
と![]() の間の一対一対応であり,
の間の一対一対応であり,![]() の直線を
の直線を![]() の直線にうつす.
つまり
の直線にうつす.
つまり![]() に対して
に対して
共線写像は,独立な点集合を独立な点集合にうつし,枠を枠にうつす.
また四角性六点を四角性六点にうつす.
よって直線体![]() と
と
![]() の同型を定める.
の同型を定める.
射影空間![]() の共線変換の集合は
の共線変換の集合は![]() の変換群をつくる.
これを
の変換群をつくる.
これを
![]() で表す.
で表す.
証明
すでに![]() の部分空間
の部分空間![]() に対しては配景写像の合成として射影写像が定義されていた.注意3.1.2にあるように,
に対しては配景写像の合成として射影写像が定義されていた.注意3.1.2にあるように,![]() そのものの射影写像は未定義であった.
直線体と射影座標の存在から,より大きい次元の空間に埋め込むことで,これを定義した.
そのものの射影写像は未定義であった.
直線体と射影座標の存在から,より大きい次元の空間に埋め込むことで,これを定義した.
この証明に補題を一つ必要とする. 以下において同座標対応は次の意味で用いる.
二つの射影空間![]() と
と![]() があり,
それぞれ同次座標が定まっているとする.
があり,
それぞれ同次座標が定まっているとする.
![]() の点
の点![]() が座標
が座標![]() で表されるとき,
で表されるとき,
![]() の点でその座標が
の点でその座標が![]() で表されるものを
で表されるものを![]() とする.
これによって
とする.
これによって![]() から
から![]() への写像が定まる.
これは明らかに一対一対応である.
この写像による点対応を同座標対応という.
への写像が定まる.
これは明らかに一対一対応である.
この写像による点対応を同座標対応という.
同座標対応を
![]() とする.
これは
とする.
これは
![]() に対応する
に対応する![]() 上の点と,
枠
上の点と,
枠![]() に関する
に関する![]() の同次座標が
の同次座標が
![]() である点を対応させる.
これに対して,
である点を対応させる.
これに対して,
![]() を中心とする配景写像を
を中心とする配景写像を
![]() とし,
これによって
とし,
これによって
![]() に対応する
に対応する![]() 上の点が,
上の点が,
![]() に対応する
に対応する![]() 上の点に対応するとする.
上の点に対応するとする.
![]() なる
なる![]() 上の一次変換を
上の一次変換を![]() とする.
命題49よりこれは射影写像である.このとき
とする.
命題49よりこれは射影写像である.このとき
![]() なので,
なので,![]() は射影写像である.
□
は射影写像である.
□
命題61の証明
命題47により変換
![]() は
は![]() の各辺の直線体に対しては内部自己同型である.つまり命題60の
の各辺の直線体に対しては内部自己同型である.つまり命題60の![]() が
が![]() にとれる.したがって
にとれる.したがって
![]() となり
となり
![]() である.
である.
逆に![]() の任意の直線
の任意の直線
![]() は
は
![]() により直線
により直線
![]() にうつる.補題14より同座標対応
にうつる.補題14より同座標対応
![]() は射影写像である.
□
は射影写像である.
□
証明 変換(3.3)が共線変換であることは明らか.
![]() の直線
の直線
![]() は変換(3.4)
で直線
は変換(3.4)
で直線
射影変換で枠を動かさないもの
![]() は
は![]() であるから,すべての射影変換は
変換(3.4)と内部自己同型の結合である.
命題61の後半より,それもまた変換(3.4)の形に書ける.
であるから,すべての射影変換は
変換(3.4)と内部自己同型の結合である.
命題61の後半より,それもまた変換(3.4)の形に書ける.
次に共線変換
![]() をとる.
をとる.![]() は枠
は枠![]() を
を![]() に移すとする.
枠
に移すとする.
枠![]() を枠
を枠![]() に移す射影変換
に移す射影変換![]() をとる.射影変換は共線変換であるから
をとる.射影変換は共線変換であるから
![]() は枠
は枠![]() を動かさない共線変換であり,
を動かさない共線変換であり,
![]() に属する.
よって一般の共線変換は,
に属する.
よって一般の共線変換は,
![]() と射影変換
と射影変換
![]() の合成になる.
それが変換(3.3)である.
□
の合成になる.
それが変換(3.3)である.
□
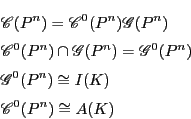
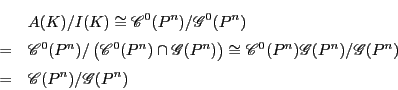
これから射影空間![]() の共線変換が射影変換であるための必要十分条件は
係数体が内部自己同型以外の同型をもたないことであるがわかる.
の共線変換が射影変換であるための必要十分条件は
係数体が内部自己同型以外の同型をもたないことであるがわかる.
実数体は命題29によって恒等変換以外に自己同型をもたないので,共線変換はすべて射影変換である.複素数体ではそれは成り立たない.
射影空間![]() についての条件(2)を射影幾何の基本定理といった.
直線体が実数体
についての条件(2)を射影幾何の基本定理といった.
直線体が実数体![]() や複素数体
や複素数体![]() においては,射影幾何の基本定理が成り立つ.
においては,射影幾何の基本定理が成り立つ.
歴史的には,係数体を実数体とする射影幾何が研究された. この場においては条件(2)が成り立つ. したがって研究の中で射影変換の一意の存在が発見され, これが基本定理とされたのである.
しかし公理系から出発した結果,この条件の成り立つ根拠が明らかになり, 上記3命題の同値性こそが基本定理となったのである.