

 次: 円錐曲線
上: 二次曲面の定義
前: 線型代数の準備
次: 円錐曲線
上: 二次曲面の定義
前: 線型代数の準備
 の係数体はこれまでと同様に可換とし,さらにその標数は2でないとする.必要に応じて
の係数体はこれまでと同様に可換とし,さらにその標数は2でないとする.必要に応じて は代数的閉体とするが,それはそれを必要とするところで指示する.以下
は代数的閉体とするが,それはそれを必要とするところで指示する.以下 次元射影空間における
次元射影空間における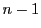 次曲面を考えるので,超平面にならえば「超曲面」というべきところであるが,高次の場合も含めて「曲面」で統一する.
次曲面を考えるので,超平面にならえば「超曲面」というべきところであるが,高次の場合も含めて「曲面」で統一する.
定義 29 (極系による定義)

次元射影空間

からその双対空間

への射影写像
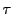
が極系であるとする.

の点

に対し
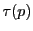
は

の点であり
双対対応によって

の超平面に対応する.

の点集合
を,極系
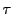
で定まる二次曲面という.
■
射影空間 で枠
で枠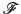 を選び座標系
を選び座標系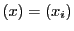 が定まっているとする.
この座標系に関して
が定まっているとする.
この座標系に関して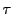 は
は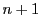 次の対称行列の類で表される.
行列はこの類の代表であると考える.つまり行列
次の対称行列の類で表される.
行列はこの類の代表であると考える.つまり行列 は
は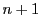 次正方行列を0でない定数倍の同値関係で類別した類の要素を表すものとする.
次正方行列を0でない定数倍の同値関係で類別した類の要素を表すものとする.
 の座標を
の座標を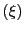 とする.
これは縦ベクトルであった.
とする.
これは縦ベクトルであった.
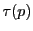 は
は の座標で行列との積
の座標で行列との積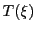 になる.
これが
になる.
これが の超平面
の超平面
を定める.二次曲面の定義を座標系でいえば,
点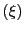 が
が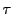 で定まる二次曲面の点であることは,
で定まる二次曲面の点であることは,
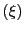 が再びこの方程式を満たすということである.
つまり
が再びこの方程式を満たすということである.
つまり
を満たす点の集合が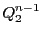 である.
である.
射影写像は一対一対応であり,その行列 の階数は
の階数は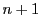 である.
ここの部分を一般化し,一般の対称行列によって
二次曲面を定義することができる.
である.
ここの部分を一般化し,一般の対称行列によって
二次曲面を定義することができる.
定義 30 (対称行列による定義)

の座標系
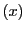
がある.

を必ずしも階数が
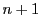
とはかぎらない対称行列とする.
座標系の方程式
を満たす

の点の集合を二次曲面といい
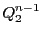
と表す.
■
これは先の曲系による定義29を含む.
つまり の階数が
の階数が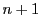 なら同等の定義である.
なら同等の定義である.
今後,この一般化された定義を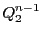 の定義とする.
線型代数の一般論から,
対称行列
の定義とする.
線型代数の一般論から,
対称行列 に対して
に対して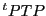 が対角行列となるような
可逆行列
が対角行列となるような
可逆行列 が存在する.
この証明は『線型代数の考え方』など参照のこと.
これからただちに次のことが結論される.
が存在する.
この証明は『線型代数の考え方』など参照のこと.
これからただちに次のことが結論される.
命題 75

次元射影空間におかれた二次曲面は,
座標系をつまりは枠を適当に選ぶことによって
と表される.
■
系 75.1

が代数的閉体なら
に帰着する.

が実数体なら
に帰着する.
■
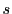 は行列
は行列 の階数である.
の階数である.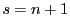 のとき二次曲面は正則であるという.
あるいはまた非退化であるという.
のとき二次曲面は正則であるという.
あるいはまた非退化であるという.
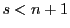 のときは非正則,あるいは退化であるという.
このとき
のときは非正則,あるいは退化であるという.
このとき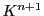 の要素で
の要素で
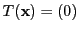 となるものは,
となるものは,
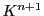 の部分空間をなす.
このときこれに対応して,
の部分空間をなす.
このときこれに対応して,
 の部分空間でその要素
の部分空間でその要素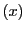 が
が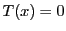 となるものが存在する.
これを二次曲面の特異空間,その要素を特異点という.
となるものが存在する.
これを二次曲面の特異空間,その要素を特異点という.
二次曲線で特異点の集合が直線であれば
その方程式は因数分解される.
逆に因数分解されれば2直線となる.
例 4.1.1
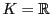
の

において
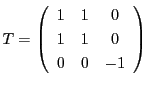
とおく.

の階数は2である.
このとき同次座標で
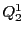
の方程式は
と因数分解される.したがって
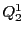
は2直線を表す.
注意 4.1.1
代数幾何学においては,曲線の特異点が定義される.
特異点をもたない曲線を
滑らか,あるいは
非特異という.
2次曲線においては,非退化であることと非特異であることが同値である.
この証明などは,『Poncelet's Theorem』[
40]の定理3.2 を参照のこと.
射影空間 からその双対空間
からその双対空間 への射影写像
への射影写像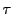 が極系であるとき,
が極系であるとき,
 の点
の点 に対して
に対して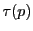 は
は の点であり
の点であり の超平面を定める.
の超平面を定める. によって定まる
によって定まる の超平面を
の超平面を の極超平面といい同じ
の極超平面といい同じ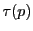 で表す.
で表す.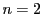 の場合は極線という.逆に
の場合は極線という.逆に の要素である
の要素である の超平面
の超平面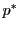 に対して
に対して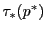 は
は の点である.これを
の点である.これを の超平面
の超平面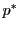 の極という.
の極という.
 の点
の点 とその双対空間の点,
すなわち
とその双対空間の点,
すなわち の超平面
の超平面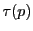 の上にある点
の上にある点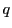 は
は
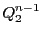 に関し共役であるという.
それぞれの座標を
に関し共役であるという.
それぞれの座標を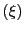 と
と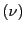 とする.
とする.
 が
が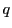 と共役なら
と共役なら
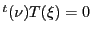 である.
である.
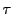 に対応する行列は対称なのでこれは
に対応する行列は対称なのでこれは
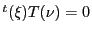 と同値である.
よって
と同値である.
よって が
が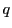 と共役なら
と共役なら
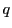 が
が と共役である.
と共役である.
二次曲面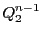 上の点
上の点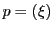 は
は
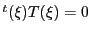 を満たすので,それ自身に共役,つまり自己共役である.
を満たすので,それ自身に共役,つまり自己共役である.
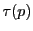 が定める超平面を点
が定める超平面を点 における
における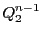 の接超平面という.
の接超平面という.
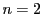 のときは接線という.
のときは接線という.
命題 76
射影写像
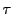
を極系としそれが定める二次曲線を
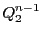
とする.

の直線

がある.

上の点で
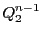
上にはない点

に対して,
超平面
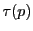
と直線

の交点を
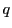
とする.
点対
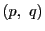
は,

によって決まり

のとり方によらない一定の対合によって対合をなす.
■
証明
 と
と に座標系を定め,それによって
に座標系を定め,それによって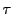 が定める行列を
が定める行列を とする.
定義28より
とする.
定義28より は対称行列である.
直線
は対称行列である.
直線 上の2定点
上の2定点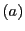 と
と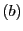 をとり,
をとり,
 を媒介変数
を媒介変数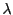 と
と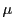 を用いて
を用いて
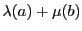 と表す.
と表す.
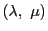 を直線
を直線 の同次座標とする.
の同次座標とする.
であるとする.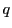 は
は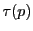 上の点なので
上の点なので
である. が対称なので
が対称なので
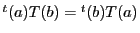 .
よってこの等式は
.
よってこの等式は
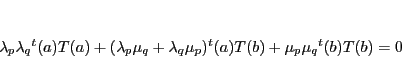 |
(4.1) |
となる.
これは命題71の等式そのものであり,
その係数
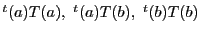 は
は と
と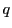 によらない.
よって条件を満たす
によらない.
よって条件を満たす 上の2点
上の2点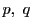 は同一の対合で対合をなす.
□
は同一の対合で対合をなす.
□
証明
(i)
命題76の直線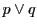 を
を とし,定点
とし,定点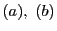 として
2点
として
2点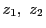 をとる.これによって点
をとる.これによって点 と
と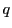 は対合をなす.
さらに方程式4.1は
は対合をなす.
さらに方程式4.1は
となる.この方程式は
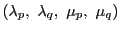 を
を
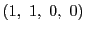 か
か
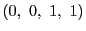 にとっても成り立ち,
この対合に関して
にとっても成り立ち,
この対合に関して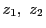 は自己対合をなすことがわかる.
命題73より
は自己対合をなすことがわかる.
命題73より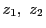 は
は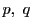 を調和に分ける.
つまり4点
を調和に分ける.
つまり4点
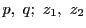 は調和列点をなす.
は調和列点をなす.
(ii)
点 は自己対合点である.
は自己対合点である.
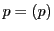 ,
,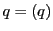 とし
とし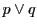 上の点
上の点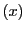 を
を
とおく.これが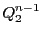 上にあるのは
上にあるのは
を満たすことであるが,
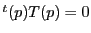 かつ
かつ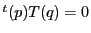 なので
これを満たすのは
なので
これを満たすのは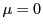 のみである.
つまり直線
のみである.
つまり直線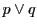 と
と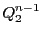 は点
は点 のみ共有する.
のみ共有する.
(iii)
同様に と
と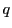 の座標を
の座標を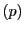 ,
,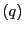 とし,
直線
とし,
直線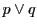 上の点
上の点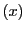 を座標系で
を座標系で
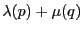 とする.
とする.
より
なので,直線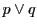 は
は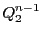 に含まれる.
に含まれる.
逆について.(i)は命題73によって と
と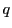 は対合をなし,
命題76によって
は対合をなし,
命題76によって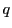 が
が と共役なら対合をなすが,
直線上の点で
と共役なら対合をなすが,
直線上の点で とその対合で対合をなす点は一意なので,
とその対合で対合をなす点は一意なので,
 と
と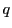 は共役である.他は明らか.
□
は共役である.他は明らか.
□
例 4.1.2 
上記定理の(i)は,ユークリッド平面では
とも定式化される.
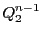 に含まれる部分空間を母空間,1次元直線の場合母線
という.
に含まれる部分空間を母空間,1次元直線の場合母線
という.
実数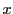 に対して
に対して![$[x]$](images/img2098.gif) は
は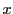 を超えない最大の整数を表すものとする.
を超えない最大の整数を表すものとする.
命題 77
複素数体
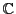
上の正則二次曲面
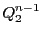
は
![$\left[\dfrac{n-1}{2} \right]$](images/img2099.gif)
次元部分空間を含む.
■
証明
系75.1から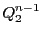 は適当な座標系によって
は適当な座標系によって
と表される.
 が奇数のとき.
が奇数のとき.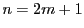 とおく.
とおく.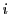 を虚数単位として
を虚数単位として
であるから,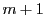 個の方程式
個の方程式
で定義される部分空間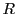 は
は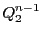 に含まれる.
に含まれる.
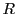 の次元は
の次元は
である.
 が偶数のとき.
が偶数のとき.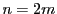 とおく.
同様に
とおく.
同様に
であるから,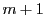 個の方程式
個の方程式
で定義される部分空間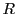 は
は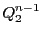 に含まれる.
に含まれる.
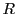 の次元は
の次元は
である.
よっていずれの場合も命題は成立する.
□
本定理は直線体 が代数的閉体であれば成り立つ.
が代数的閉体であれば成り立つ.
 の相交わらない
の相交わらない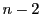 次元部分空間
次元部分空間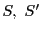 をとる.
をとる.
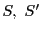 を通る超平面の集合
を通る超平面の集合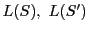 をとる.
定義14によってこれらは線型基本図形であり,
その基本図形の間の射影写像の概念が有効である.
をとる.
定義14によってこれらは線型基本図形であり,
その基本図形の間の射影写像の概念が有効である.
定義 31 (幾何的定義)

の相交わらない
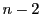
次元部分空間
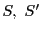
に対する超平面束
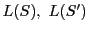
が射影的であるとき,つまり射影写像
が存在するとき,対応する超平面の共通部分空間の集合
を二次曲面という.■
 における
における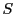 と
と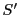 は双対的に
は双対的に の直線に対応し,
の直線に対応し,
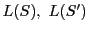 はそれらの直線上の点の集合に対応する.
はそれらの直線上の点の集合に対応する.
 において
において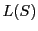 と
と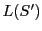 が射影的であるということと,
が射影的であるということと,
 において双対的に対応する直線から直線への射影写像
において双対的に対応する直線から直線への射影写像 が存在することが同値である.
が存在することが同値である.
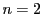 のとき,
のとき,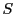 と
と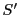 は異なる点
は異なる点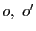 であり,
であり,
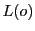 ,
,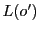 はそれぞれ
はそれぞれ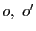 をとおる直線の集合である.
これを母線束という.
定義30と定義31が同等であることは次のように示される.
をとおる直線の集合である.
これを母線束という.
定義30と定義31が同等であることは次のように示される.
証明
 (I)
(I)
 と
と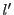 の交点の座標を
の交点の座標を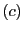 とすると
とすると
であり,媒介変数
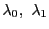 ,
,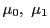 を用いて
を用いて
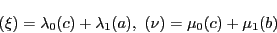
と表される.さらに直線
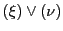 上の点は
媒介変数
上の点は
媒介変数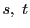 を用いて
を用いて
と表される.これが と接しているので
と接しているので
が同次二次方程式として重根をもつ.
よって
である.
よって判別式の条件は
これから
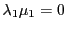 つまり
つまり が
が か
か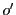 に一致するか,
または
に一致するか,
または
これは変換行列が
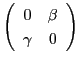 型の射影写像である.
型の射影写像である.
注意 4.1.2
1)
この対応は明らかに

から
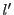
への一対一対応である.
かつ代数的に対応している.

が代数的閉体ならここから射影写像でしかありえないことがわかる.
閉体でない場合を含め示した.
2)
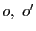
は二次曲線上の異なる2点であればつねに成りたつ.
(II)
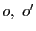 の座標を
の座標を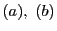 とする.
とする.
である. が行列
が行列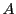 で表されるとする.つまり
で表されるとする.つまり
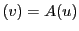 とする.
とする. の座標を
の座標を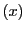 とすると,
とすると,
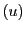 の成分には0でないものがあるので,
三つの縦ベクトル
の成分には0でないものがあるので,
三つの縦ベクトル
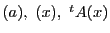 より構成される3次正方行列式について
より構成される3次正方行列式について
が成り立つ.これを成分で書き表し整理すれば,
になる.
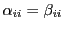 ,
,
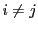 のとき
のとき
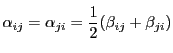 で
で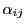 を定める.
このとき
を定める.
このとき
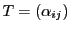 で定まる対称行列
で定まる対称行列 による二次曲線
による二次曲線 が
が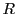 に一致する.
□
に一致する.
□
注意 4.1.3
2次元の場合に3次行列よる定義と古典的定義の同等性が示された.
高次の場合についての二つの定義の関係は今後の研究課題とする.
命題 79
平面二次曲線が2直線に分解されることと,
幾何的定義における射影写像
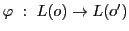
が配景写像であることは
同値である.
■
証明
射影写像 が配景写像であるとする.
双対空間での配景の中心に対応する
が配景写像であるとする.
双対空間での配景の中心に対応する の直線を
の直線を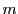 とする.
直線
とする.
直線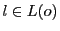 と
と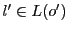 は
は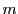 上の点で交わることを意味する.
また
上の点で交わることを意味する.
また によって直線
によって直線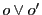 はそれ自身にうつる.
よって
はそれ自身にうつる.
よって は
は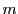 と
と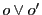 それ自身である.
それ自身である.
2直線に分解されるとする.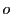 と
と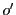 は互いにうつるので,
2直線になればそのうちの1本は
は互いにうつるので,
2直線になればそのうちの1本は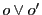 であり,
他方の直線の双対空間での点は配景の中心である.
□
であり,
他方の直線の双対空間での点は配景の中心である.
□


 次: 円錐曲線
上: 二次曲面の定義
前: 線型代数の準備
2014-01-03
次: 円錐曲線
上: 二次曲面の定義
前: 線型代数の準備
2014-01-03
![]() で枠
で枠![]() を選び座標系
を選び座標系![]() が定まっているとする.
この座標系に関して
が定まっているとする.
この座標系に関して![]() は
は![]() 次の対称行列の類で表される.
行列はこの類の代表であると考える.つまり行列
次の対称行列の類で表される.
行列はこの類の代表であると考える.つまり行列![]() は
は![]() 次正方行列を0でない定数倍の同値関係で類別した類の要素を表すものとする.
次正方行列を0でない定数倍の同値関係で類別した類の要素を表すものとする.
![]() の座標を
の座標を![]() とする.
これは縦ベクトルであった.
とする.
これは縦ベクトルであった.
![]() は
は![]() の座標で行列との積
の座標で行列との積![]() になる.
これが
になる.
これが![]() の超平面
の超平面
![]() の階数は
の階数は![]() である.
ここの部分を一般化し,一般の対称行列によって
二次曲面を定義することができる.
である.
ここの部分を一般化し,一般の対称行列によって
二次曲面を定義することができる.
![]() の階数が
の階数が![]() なら同等の定義である.
なら同等の定義である.
![]() の定義とする.
線型代数の一般論から,
対称行列
の定義とする.
線型代数の一般論から,
対称行列![]() に対して
に対して![]() が対角行列となるような
可逆行列
が対角行列となるような
可逆行列![]() が存在する.
この証明は『線型代数の考え方』など参照のこと.
これからただちに次のことが結論される.
が存在する.
この証明は『線型代数の考え方』など参照のこと.
これからただちに次のことが結論される.
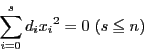
![]() は行列
は行列![]() の階数である.
の階数である.![]() のとき二次曲面は正則であるという.
あるいはまた非退化であるという.
のとき二次曲面は正則であるという.
あるいはまた非退化であるという.
![]() のときは非正則,あるいは退化であるという.
このとき
のときは非正則,あるいは退化であるという.
このとき![]() の要素で
の要素で
![]() となるものは,
となるものは,
![]() の部分空間をなす.
このときこれに対応して,
の部分空間をなす.
このときこれに対応して,
![]() の部分空間でその要素
の部分空間でその要素![]() が
が![]() となるものが存在する.
これを二次曲面の特異空間,その要素を特異点という.
となるものが存在する.
これを二次曲面の特異空間,その要素を特異点という.
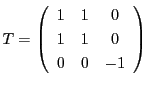 とおく.
とおく.![]() の点
の点![]() とその双対空間の点,
すなわち
とその双対空間の点,
すなわち![]() の超平面
の超平面![]() の上にある点
の上にある点![]() は
は
![]() に関し共役であるという.
それぞれの座標を
に関し共役であるという.
それぞれの座標を![]() と
と![]() とする.
とする.
![]() が
が![]() と共役なら
と共役なら
![]() である.
である.
![]() に対応する行列は対称なのでこれは
に対応する行列は対称なのでこれは
![]() と同値である.
よって
と同値である.
よって![]() が
が![]() と共役なら
と共役なら
![]() が
が![]() と共役である.
と共役である.
![]() と
と![]() は対合をなし,
命題76によって
は対合をなし,
命題76によって![]() が
が![]() と共役なら対合をなすが,
直線上の点で
と共役なら対合をなすが,
直線上の点で![]() とその対合で対合をなす点は一意なので,
とその対合で対合をなす点は一意なので,
![]() と
と![]() は共役である.他は明らか.
□
は共役である.他は明らか.
□
 上記定理の(i)は,ユークリッド平面では
上記定理の(i)は,ユークリッド平面では ![]() に対して
に対して![]() は
は![]() を超えない最大の整数を表すものとする.
を超えない最大の整数を表すものとする.
![$\left[\dfrac{n-1}{2} \right]$](images/img2099.gif) 次元部分空間を含む.
■
次元部分空間を含む.
■
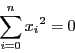
![]() が奇数のとき.
が奇数のとき.![]() とおく.
とおく.![]() を虚数単位として
を虚数単位として
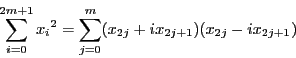
![]() が偶数のとき.
が偶数のとき.![]() とおく.
同様に
とおく.
同様に
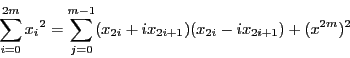
![]() が代数的閉体であれば成り立つ.
が代数的閉体であれば成り立つ.
 (I)
(I)
![]() と
と![]() の交点の座標を
の交点の座標を![]() とすると
とすると
![]()
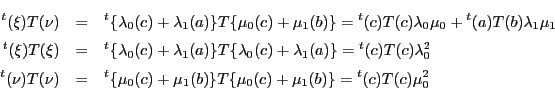
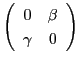 型の射影写像である.
型の射影写像である.
![]() の座標を
の座標を![]() とする.
とする.
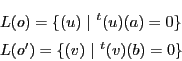
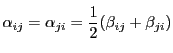 で
で![]() と
と![]() は互いにうつるので,
2直線になればそのうちの1本は
は互いにうつるので,
2直線になればそのうちの1本は![]() であり,
他方の直線の双対空間での点は配景の中心である.
□
であり,
他方の直線の双対空間での点は配景の中心である.
□