次: 線型代数による証明 上: ポンスレの定理 前: ポンスレの閉形定理

対合定理による証明

$n=3$の場合の証明

$Q_0$に内接し$Q_1$に外接する三角形$a_1a_2a_3$がある． 他方$Q_0$上の4点 $b_1,\ b_2,\ b_3,\ c$で3直線$b_1\vee b_2$， $b_2\vee b_3$，$b_3\vee c$が$Q_1$に接しているなら， $c=b_1$となることを意味する．

命題83によって 三角形$a_1a_2a_3$と三角形$b_1b_2b_3$に内接する円錐曲線$Q$が存在する． $Q$と$Q_1$は 三角形$a_1a_2a_3$の接点，$b_1\vee b_2$，$b_2\vee b_3$の接点の5点を共有している． 命題82によって5点を指定すれば円錐曲線は一意に定まるので， $Q=Q_1$である．

よって$c=b_1$となり， 任意の点についてそれを頂点の一つとする同様の三角形が存在する． □

$n=4$の場合の証明

$Q_0$に内接し$Q_1$に外接する四角形$a_1a_2a_3a_4$がある． 他方$Q_0$上の5点 $b_1,\ b_2,\ b_3,\ b_4,\ c$で4直線 $b_1\vee b_2$，$b_2\vee b_2$，$b_3\vee b_4$，$b_4\vee c$が$Q_1$に接するなら， $c=b_1$となることを意味する．

命題87.1によって

$$[b_2\vee a_1,\ b_2\vee a_2;\ b_2\vee b_1 ,\ b_2\vee b_3]= [b_2\vee a_3,\ b_2\vee a_4;\ b_2\vee b_3,\ b_2\vee b_1]$$

が成立し，直線対

$$(b_2\vee a_1,\ b_2\vee a_3),\ (b_2\vee a_2,\ b_2\vee a_4),\ (b_2\vee b_1,\ b_2\vee b_3)$$

が対合をなす． これを$Q_0$上でみれば点対

$$(b_1,\ b_3),\ (a_1,\ a_3),\ (a_2,\ a_4)$$

は対合をなす．よって命題86によって 3直線

$$b_1\vee b_3,\ a_1\vee a_3,\ a_2\vee a_4$$

は共線である．この点を$o$とする．

     $b_2$に代えて$b_4$をとることにより

$$b_4\vee c,\ a_1\vee a_3,\ a_2\vee a_4$$

は共点である．よって$b_3\vee c$も点$o$を通り，$c=b_1$である． □

一般の場合の証明

ポンスレの閉形定理11を， 曲線束を用いてやや一般的な形で定式化し，それを証明する． 曲線束はポンスレ自身の基本的な方法だった． そのためにいくつかの命題を示す．

命題 97        円錐曲線$Q_0$に内接する四辺形$abcd$の辺 $a\vee b,\ c\vee d$と円錐曲線$Q_1$が接するとき， $Q_0,\ Q_1$で定まる曲線束に属する円錐曲線$Q_2$で 辺 $a\vee c,\ b\vee d$と接するものが存在する． ■

証明      $Q_0,\ Q_1$の4交点を $\{\alpha,\ \beta,\ \gamma,\ \delta \}$ とする．これらの中に同じものがあってもよい． また $\{\alpha,\ \beta,\ \gamma,\ \delta \}$で定まる曲線束を$A$， $\{a,\ b,\ c,\ d \}$で定まる曲線束を$B$とする．

(1)     $\{a,\ b,\ c,\ d \}$の中に異なるものが3個以上ある場合．

     $a\vee b,\ c\vee d$と$Q_1$の接点を$p,\ p'$とし，$l=p\vee p'$とする． $l$と$b\vee c$，$a\vee d$の交点をそれぞれ$q,\ q'$とし， さらに$l$と$Q_0$との交点を$\{r,\ r'\}$， $b\vee c$と$Q_1$との交点を$\{s,\ s'\}$とする．

点$q$は$Q_0,\ Q_1$上にないので，曲線束$A$の要素で， 点$q$を通るものが一意に存在する． これを$Q_2$とする．

デザルグの対合定理86の証明を 曲線束$B$に適用して，三つの点対

$$(p,\ p'),\ (q,\ q'),\ (r,\ r')$$

は同一の対合に属する．曲線束$A$にデザルグの対合定理86の証明を適用すると，点対 $(p,\ p'),\ (r,\ r')$で定まる対合で，点$q$と対合となる点が定まるが，2点の対応を定めれば対合は一意なので，この点が$q'$に他ならない． よって$Q_2$は$q'$を通る．

次に円錐曲線$Q_2$は点$q,\ q'$で$b\vee c$，$a\vee d$と接することを示す．再びデザルグの対合定理の証明と同様にして

$$\begin{eqnarray*}[q,\ c;\ s,\ s']&=&[p'\vee q,\ p'\vee c;\ p'\vee s,\ p'\vee s']... ...ee p';\ p\vee s,\ p\vee s']= [b,\ q;\ s,\ s']=[q,\ b;\ s',\ s] \end{eqnarray*}$$

よって点対 $(b,\ c),\ (s,\ s')$で定まる対合に関して$q$は自己対合である．点対 $(b,\ c),\ (s,\ s')$で定まる対合は曲線束$A$を$b\vee c$で切った直線上の対合でもある．よって$q$は$Q_2$上の点としてこの対合で自己対合である．つまり$Q_2$は$q$で$b\vee c$に接する． $q'$についても同様である．

この証明は$a=b$の場合もそのまま通用する．他の2点が一致するときは， 点の名前をつけ替えればよい．

また $\alpha,\ \beta,\ \gamma,\ \delta$に同じものがあるときも証明はそのままでよい． 例えば$Q_0$と$Q_1$が3重に接している場合もこの証明の中で示せている．

(2)    $a=b,\ c=d$の場合．

    2直線$a\vee c$と$p\vee p'$の交点を$q$とする． (1)の証明の後半と同様に， $(a,\ c),\ (s,\ s')$で定まる対合に関して$q$は自己対合である． 一方， 2直線 $\alpha\vee \gamma$， $\beta\vee \delta$の積は曲線束$A$に属する分解した二次曲線である． 曲線束$A$の直線$a\vee c$上の対合に関して 2直線 $\alpha\vee \gamma$， $\beta\vee \delta$の積の自己対合点はその交点である． よって$q$は2直線 $\alpha\vee \gamma$， $\beta\vee \delta$の交点と一致する． かくして2直線 $\alpha\vee \gamma$， $\beta\vee \delta$の積が 直線$a\vee c$と1点を共有し，これが求める$Q_2$である．

その他の点が一致する場合，つまり右図のようになるときもあるが， その場合の証明は同じである． □

円に還元する別証明

$Q_0$と$Q_1$の4交点のうち 2点を射影変換で点 $(1,\ \pm i,\ 0)$にうつす． このとき，$Q_0$と$Q_1$を実平面で切ると2円が得られる． 直線と点の共線，共点の関係は，実平面を距離空間と見なしても同様である． 対応する実平面上の点は大文字で表す． また二直線$\mathrm{AB}$と$\mathrm{CD}$のなす角を $\angle(\mathrm{AB},\ \mathrm{CD})$のように表す．

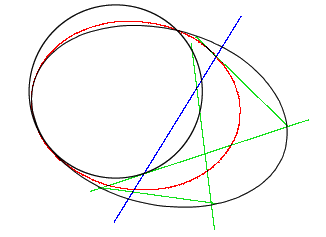
実平面の円束に関する補題を確認しよう．

補題 18        与えられた二つの円への接線の長さの比が一定値$\lambda$になる点の軌跡は， 2円で定まる円束の円である． ■

証明     2円を$Q_0,\ Q_1$，中心を $\mathrm{O}_0,\ \mathrm{O}_1$とし，その方程式を

$$\begin{eqnarray*} Q_0&:&(x-a_0)^2+(y-b_0)^2-{r_0}^2=0\\ Q_1&:&(x-a_1)^2+(y-b_1)^2-{r_1}^2=0 \end{eqnarray*}$$

とする．点 $\mathrm{P}(X,\ Y)$から$Q_0,\ Q_1$への接点を $\mathrm{T}_0,\ \mathrm{T}_1$とする． 三平方の定理から

$$\begin{eqnarray*} \mathrm{PT}_0^2=P\mathrm{O}_0^2-{r_0}^2=(X-a_0)^2+(Y-b_0)^2-{... ...hrm{PT}_1^2=P\mathrm{O}_1^2-{r_1}^2=(X-a_1)^2+(Y-b_1)^2-{r_1}^2 \end{eqnarray*}$$

よって$(X,\ Y)$の条件は方程式

$$(X-a_0)^2+(Y-b_0)^2-{r_0}^2+\lambda^2\{(X-a_1)^2+(Y-b_1)^2-{r_1}^2\}=0$$

をみたすこととなり，点$\mathrm{P}$の軌跡は方程式

$$(x-a_0)^2+(y-b_0)^2-{r_0}^2+\lambda^2\{(x-a_1)^2+(y-b_1)^2-{r_1}^2\}=0$$

である．これは点$\mathrm{P}$の軌跡が2円で定まる円束の円であることを示している． 　□

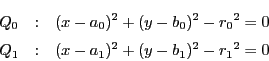
これから次のような別証明ができる．

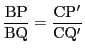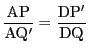円周角の定理によって $\angle(\mathrm{BQ},\ \mathrm{BP})=\angle(\mathrm{CQ'},\ \mathrm{CP'})$， $\angle(\mathrm{PB},\ \mathrm{PQ})=\angle(\mathrm{P'C},\ \mathrm{P'Q'})$である． よって三角形$\mathrm{BPQ}$と $\mathrm{CP'Q'}$は相似であり $\dfrac{\mathrm{BP}}{\mathrm{BQ}}=\dfrac{\mathrm{CP'}}{\mathrm{CQ'}}$である． 同様にして 三角形$\mathrm{APQ'}$と$\mathrm{DP'Q}$は相似であり $\dfrac{\mathrm{AP}}{\mathrm{AQ'}}=\dfrac{\mathrm{DP'}}{\mathrm{DQ}}$である．

三角形の正弦定理から

$$\dfrac{\mathrm{BQ}}{\sin\angle(\mathrm{PB},\ \mathrm{PQ})}=... ...\dfrac{\mathrm{AP}}{\sin\angle(\mathrm{Q'P'},\ \mathrm{Q'C})}$$

これより

$$\dfrac{\mathrm{BP}}{\mathrm{BQ}}=\dfrac{\mathrm{AP}}{\mathrm{AQ'}},\$$

以上から

$$\dfrac{\mathrm{BP}}{\mathrm{BQ}}=\dfrac{\mathrm{CP'}}{\math... ...{\mathrm{AP}}{\mathrm{AQ'}}=\dfrac{\mathrm{DP'}}{\mathrm{DQ}}$$

直線$\mathrm{AC}$と$\mathrm{BD}$の交点を$\mathrm{M}$とすると， 三角形$\mathrm{MQQ'}$は二等辺三角形で $\mathrm{MQ}=\mathrm{MQ'}$となる．よって 2点 $\mathrm{Q},\ \mathrm{Q'}$で $\mathrm{MQ},\ \mathrm{MQ'}$に接する円$Q_2$が存在する．

$Q_0$上の4点 $\mathrm{A},\ \mathrm{B},\ \mathrm{C},\ \mathrm{D}$から$Q_1,\ Q_2$への 接線の長さの比はすべて等しく．円$Q_0$は$Q_1$，$Q_2$と同じ円束に属する．いいかえれば$Q_2$は円$Q_0$は$Q_1$で定まる円束の円である．

$a=b,\ c=d$の場合は$Q_0$と$Q_1$の他の2共有点を結ぶ直線が平行となり， 2虚点を結ぶ無限遠直線$z=0$の4直線が共点となることから示される． □

このようにして円の場合に証明されたことを， 射影変換でもとに戻すことにより， 一定の条件を満たす任意の円錐曲線での命題が示される．

ポンスレの定理

ポンスレの定理といわれる，射影幾何の曲線束に関する定理を証明し， それにもとずく閉形定理の証明をおこなおう． これがポンスレの基本的な方法であった．

命題 98       曲線束$A$に属する円錐曲線 $Q_0,\ Q_1,\ Q_2$がある． $i=1,\ 2$に対し， $Q_0$上の点$p$から$Q_i$に接線$l_i$を引く． $Q_0$の点$q_i$で$l_i=p\vee q_i$となるものをとる． このとき直線$q_1\vee q_2$と接する曲線束$A$の円錐曲線$Q_3$ が存在する． ■

証明      $Q_0$には$p$と異なる点が存在するので，他の点$p'$をとる． $i=1,\ 2$に対し， 点$p'$から$Q_i$に接線${l_i}'$を引く． $Q_0$の点${q_i}'$で ${l_i}'=p'\vee {q_i}'$となるものをとる．

$i=1,\ 2$に対し， $p\vee q_i$と$p'\vee {q_i}'$がともに$Q_i$に接するので， 定理97より $p\vee p'$と $q_1\vee {q_1}'$が接する曲線束の円錐曲線と $p\vee p'$と $q_2\vee {q_2}'$が接する曲線束の円錐曲線が存在する．$p\vee p'$に接する曲線束の要素は一意に定まるので， これらの円錐曲線は同一である．これを$Q'$とする． $q_1\vee {q_1}'$と $q_2\vee {q_2}'$がともに$Q'$に接するので， 再び定理97より直線$q_1\vee q_2$が接する曲線束$A$の円錐曲線$Q_3$が存在する． □

定理 12 (ポンスレの定理)       自然数$n$を$n\ge 3$とする． 与えられた円錐曲線$Q_0$上に頂点をもつ$n$角形 $a_1a_2\cdots a_n$がある． 辺 $a_1\vee a_2,\ \cdots,\ a_{n-1}\vee a_n$はそれぞれ$Q_0$と同じ曲線束に属する 円錐曲線 $Q_1,\ Q_2,\ \cdots ,\ Q_{n-1}$に接している． このとき残る辺$a_n\vee a_1$も同じ曲線束に属するある円錐曲線$Q$に接する． ■

証明      この曲線束を$A$とする． $n$に関する数学的帰納法で示す． $n=3$のときは，命題98において，$p,\ q_1,\ q_2$を $a_2,\ a_1,\ a_3$とすることによって， $a_3\vee a_1$が接する$A$の要素が存在することが示された．

$n-1$のとき成立するとする． $a_{n-1}\vee a_1$が接する曲線束$A$に属する円錐曲線$Q'$が存在する． 一方 $a_{n-1}\vee a_n$は$Q_{n-1}$に接している． 命題98において，$p,\ q_1,\ q_2$を $a_{n-1},\ a_n,\ a_1$とすることによって， $a_n\vee a_1$が接する$A$の要素が存在することが示された．

よって$n\ge 3$に対してつねに成立する． □

このポンスレの定理を根拠として，閉形定理が示される．

定理 13 (閉形定理)        自然数$n$を$n\ge 3$とする． 与えられた円錐曲線$Q_0$上に頂点をもつ$n$角形 $a_1a_2\cdots a_n$で， 辺 $a_1\vee a_2,\ \cdots,\ a_{n-1}\vee a_n,\ a_{n}\vee a_1$が 一つの円錐曲線$Q_1$に接しているものが存在する． このとき，$Q_0$上の任意の点$p_1$をとり，順次 $p_i\ (i=2,\ 3,\ \cdots,\ n)$ を $p_{i-1}\vee p_i$が$Q_1$に接するようにとる． このとき残る辺$p_n\vee p_1$も$Q_1$に接する． ■

証明      $i=2,\ 3,\ \cdots,\ n$に対して $a_{i-1}\vee a_i$と $p_{i-1}\vee p_i$が$Q_1$に接するので，定理97より $a_{i-1}\vee p_{i-1}$と $a_{i}\vee p_{i}$が同じ曲線束$A$の同じ円錐曲線に接する． 定直線に接する曲線束の要素は一意に定まるので， $a_{i}\vee p_{i}\ (i=1,\ 2,\ 3,\ \cdots,\ n)$は同じ円錐曲線$Q'$に接する． この結果，再び定理97より$p_n\vee p_1$と$a_n\vee a_1$も 同じ曲線束の同じ円錐曲線に接する．つまり$p_n\vee p_1$も$Q_1$に接することが示された． □ 次: 線型代数による証明 上: ポンスレの定理 前: ポンスレの閉形定理