

 次: パスカルの定理
上: 二次曲面の定義
前: 諸定義とその関係
次: パスカルの定理
上: 二次曲面の定義
前: 諸定義とその関係
平面二次曲線の研究は19世紀に大きく発展した.
その基本的な部分を再構成してゆこう.
係数体 は可換で標数は2でないとする.
は可換で標数は2でないとする.
 上の射影空間
上の射影空間 において座標枠を決め,座標系が導入されているものとする.
射影平面
において座標枠を決め,座標系が導入されているものとする.
射影平面 におかれた二次曲線
におかれた二次曲線 のことを円錐曲線とも言う.
円錐曲線という名称は円錐を平面で切断した切り口の図形に由来する.
それが2次式で定まる二次曲線であることが認識されるより前に,
円錐曲線としての長い研究の歴史があった.
のことを円錐曲線とも言う.
円錐曲線という名称は円錐を平面で切断した切り口の図形に由来する.
それが2次式で定まる二次曲線であることが認識されるより前に,
円錐曲線としての長い研究の歴史があった.
以下の命題の証明は,二次曲線の幾何的定義をもとにしながら,
可能なかぎり,極系による定義をもとにした証明をつけるものとする.
次の命題はシュタイーナーによる.
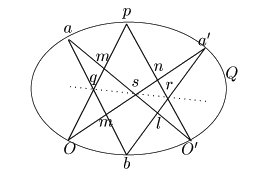
命題 80
正則二次曲線

上の任意の2点
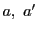
と動点

をとる.

を中心とする線束
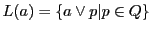
と
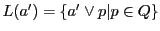
とは

の基本図形として射影的である.
ただし,動点

が

に一致したとき,
直線
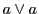
は点

における

の接線をとるものとする.
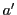
についても同様とする.
■
証明
 母線束の中心を
母線束の中心を とする.
とする.
 1)
1)
 がすべて異なるとき.
がすべて異なるとき.
 上にこれら4点と異なる
上にこれら4点と異なる をとる.図のように交点
をとる.図のように交点
 をとる.
をとる.
 の定義から
の定義から
である.これと直線
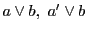 の交点をとり
の交点をとり
である.ところが点 が自対応なので,3点
が自対応なので,3点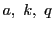 と3点
と3点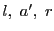 は配景的である.
よって3直線
は配景的である.
よって3直線
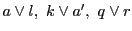 は共点である.
よって直線
は共点である.
よって直線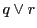 は点
は点
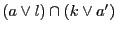 を通る.この結果
を通る.この結果
つまり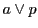 と
と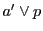 は射影的である.
は射影的である.
2) 1)以外の場合.
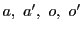 と異なる2点
と異なる2点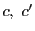 をとれば,
をとれば,
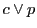 と
と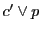 は射影的.これを改めて母線束にとれば
は射影的.これを改めて母線束にとれば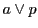 と
と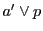 は射影的である. □
は射影的である. □
系 80.1
正則二次曲線はその上の任意の2点を母線束の中心に取ることができる.■
命題 81
正則二次曲線

上の4点
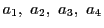
がある.

上の任意の点

をとると,
線束の複比
![$[p\vee a_1,\ p\vee a_2;\ p\vee a_3,\ p\vee a_4]$](images/img2174.gif)
が定まる.
この値は点

のとり方によらない.
■
証明
 上にいずれとも異なる点
上にいずれとも異なる点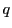 をとる.
をとる.
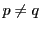 のときは
のときは と
と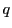 を
を の母線束の中心にとれば
の母線束の中心にとれば
もとより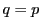 のときも成り立つので,
この値は
のときも成り立つので,
この値は によらず一定である.
□
によらず一定である.
□
証明2
命題78の(I)の証明から,
4直線
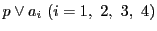 から
4直線
から
4直線
 への射影写像
への射影写像 が存在する.
定義26から,
複比
が存在する.
定義26から,
複比
![$[p\vee a_1,\ p\vee a_2;\ p\vee a_3,\ p\vee a_4]$](images/img2174.gif) は双対空間の直線上の4点の複比として定まっているが,
は双対空間の直線上の4点の複比として定まっているが,
 は双対空間の射影写像を引き起こし,
複比は射影写像で不変であるから,
複比
は双対空間の射影写像を引き起こし,
複比は射影写像で不変であるから,
複比
![$[p\vee a_1,\ p\vee a_2;\ p\vee a_3,\ p\vee a_4]$](images/img2174.gif) は点
は点 のとり方によらない.
□
のとり方によらない.
□
命題 82
射影平面

上の一般の位置にある5点
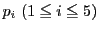
を通る
正則二次曲線がただ一つ存在する.
■
証明
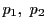 を中心とする二つの線束
を中心とする二つの線束
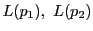 をとる.
命題35を双対空間に適用することで,
をとる.
命題35を双対空間に適用することで,
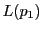 から
から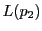 への射影写像で
への射影写像で
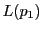 に属する3直線
に属する3直線
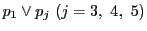 を
を
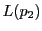 に属する3直線
に属する3直線
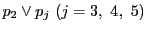 にうつすものが
ただ一つ存在する.
よって定義31より,条件を満たす二次曲線がただ一つ存在する.
□
にうつすものが
ただ一つ存在する.
よって定義31より,条件を満たす二次曲線がただ一つ存在する.
□
注意 4.1.4
本命題の証明から,5点のうちどの4点も共線でないなら二次曲線が一つに定まり,
5点が一般の位置にあるとき正則,
そうでないとき2直線に分解した二次曲線となる.
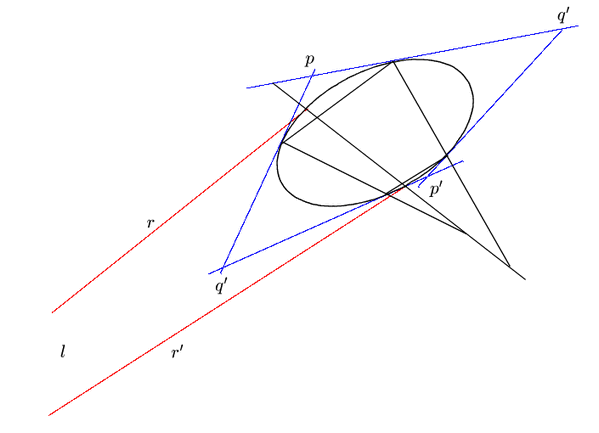
次の命題は1817年,ブリアンションによって証明された.
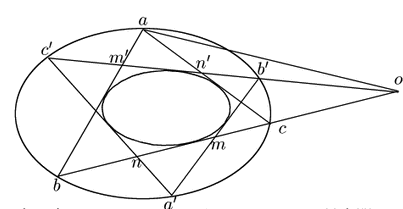
命題 83
円錐曲線

に内接する二つの三角形
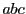
と
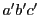
がある.
ただしどの頂点も異なるものとする.このとき二つの三角形の6辺は
ある円錐曲線
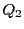
に外接する.
■
証明
点
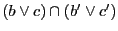 を
を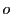 とし,
とし,
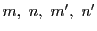 を図のように定める.
である.つまり
を図のように定める.
である.つまり
である.
 いいかえると点
いいかえると点 を中心とする線束から
点
を中心とする線束から
点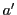 を中心とする線束への射影写像が存在する.
これがもし背景的であるとすると,点
を中心とする線束への射影写像が存在する.
これがもし背景的であるとすると,点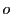 は背景写像でそれ自身に対応する.
つまり点
は背景写像でそれ自身に対応する.
つまり点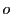 は円錐曲線
は円錐曲線 上になければならない.
これは
上になければならない.
これは
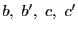 が異なるという仮定に反する.
が異なるという仮定に反する.
この結果,直線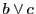 ,直線
,直線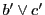 と
その上の点
と
その上の点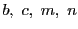 ,
,
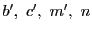 は,
双対空間で2点とそれらの点を中心とする線束となり,
かつその線束の間の射影写像が存在したので,
ある二次曲線を定める.
は,
双対空間で2点とそれらの点を中心とする線束となり,
かつその線束の間の射影写像が存在したので,
ある二次曲線を定める.
 のある平面に戻ると,それらはある二次曲線の接線となっている.
つまりこれら三角形の辺に内接する円錐曲線
のある平面に戻ると,それらはある二次曲線の接線となっている.
つまりこれら三角形の辺に内接する円錐曲線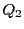 が存在する.
□
が存在する.
□
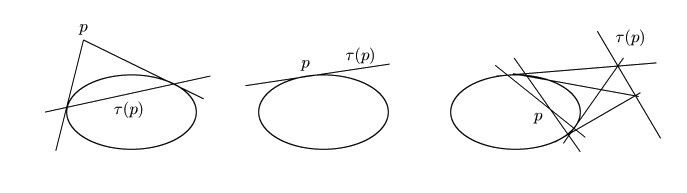
 が複素数体の場合,直線は
が複素数体の場合,直線は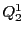 と2点で交わるか,
交点を求める方程式が重解,つまり接するかのいずれかである.
と2点で交わるか,
交点を求める方程式が重解,つまり接するかのいずれかである.
実数体の場合は次のような場合分けが起こる.
証明
点 の座標を同じく
の座標を同じく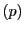 のように表す.その他の点も同様にする.
のように表す.その他の点も同様にする.
(1)
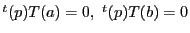 なので
極線
なので
極線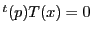 は
は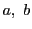 を通る.
を通る.
(2)
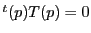 より極線
より極線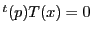 は
は を通る.
を通る.
(3)
直線 の方程式は
の方程式は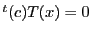 であり,
であり, はこの上にあるので
はこの上にあるので
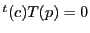 である.これは点
である.これは点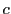 が直線
が直線
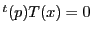 上にあることを示している.
□
上にあることを示している.
□
このように,極系による と
と の対応において,
点に対しては極線が,直線に対しては極点が対応し,
極系によって定まる正則二次曲線上の点に対しては,その接線の集合が対応する.
の対応において,
点に対しては極線が,直線に対しては極点が対応し,
極系によって定まる正則二次曲線上の点に対しては,その接線の集合が対応する.
 の他の二次曲線は,その上の点に対する極線の集合が対応し,
正則であればそれは二次曲線の包絡線となっている.
の他の二次曲線は,その上の点に対する極線の集合が対応し,
正則であればそれは二次曲線の包絡線となっている.
非正則,
つまり における2直線であれば,それは
における2直線であれば,それは の2点とそこを通る直線の集合が対応する.
の2点とそこを通る直線の集合が対応する.
二次曲線における定理9の(i)の
別証明を命題81によって行っておこう.
証明すべきことを改めて命題にする.
命題 85
一つの二次曲線 がある.
がある. 上にない点
上にない点 の極線を
の極線を とし,
とし,
 を通る任意の直線が
を通る任意の直線が および
および と交わる点を
と交わる点を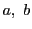 ,
,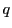 とする.
とする.
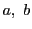 は
は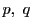 を調和に分ける.
■
を調和に分ける.
■
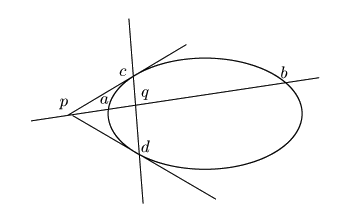 証明
点
証明
点 の極線を
の極線を とする.
実数体の場合の作図は,
とする.
実数体の場合の作図は, から
から へ2本接線が引けるときはその接点を
へ2本接線が引けるときはその接点を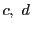 とする.
とする.
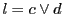 である.
または2本接線が引けないときは,
である.
または2本接線が引けないときは, から直線を引き
から直線を引き との交点を
との交点を
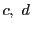 とする.このときは命題84の(2),(3)で
とする.このときは命題84の(2),(3)で が定まる.
が定まる.
命題69によって
命題81と再び命題69によって
ところが
で,点は異なり複比は1ではないので
である.
□
同次座標を
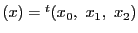 とする
とする の
円錐曲線
の
円錐曲線 が,対称行列
が,対称行列 で定まっているとする.
その方程式は
で定まっているとする.
その方程式は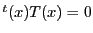 であった.
であった.
 上の点
上の点
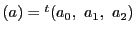 での接線の方程式は
での接線の方程式は
である. の双対空間を
の双対空間を とし,
その同次座標を
とし,
その同次座標を
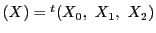 とする
この接線に対応する
とする
この接線に対応する の双対空間
の双対空間 の点は
の点は
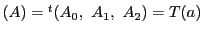 である.
である.
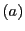 が
が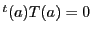 を満たすので,
を満たすので,
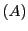 は
は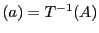 より
より
を満たす.つまり の接線の集合は
の接線の集合は において行列
において行列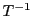 で定まる円錐曲線となる.
これを
で定まる円錐曲線となる.
これを の双対曲線といい
の双対曲線といい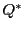 と表す.
と表す.
円錐曲線と対合に関して次の命題が基本である.
命題 86
円錐曲線

上にない定点

と,

を通る直線
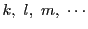
と

の共有点は,
同じ対合

に関して対合である.
逆に,円錐曲線上の対合

に関して互いに対合する点対を結ぶ直線は共点である.
■
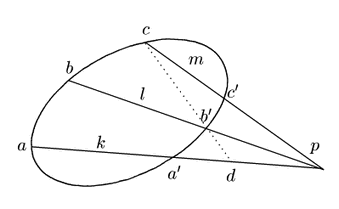 証明
図のように点
証明
図のように点 を通る任意の3線
を通る任意の3線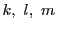 をとり,
をとり,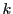 と
と を固定し,
を固定し,
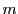 を動線と考える.これらの直線と
を動線と考える.これらの直線と の共有点を
の共有点を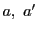 ,
,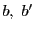 ,
,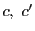 とする.
とする.
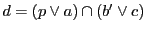 とおく.
とおく.
これは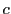 と
と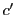 が,
が,
 と
と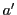 ,
, と
と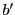 を対合対とする対合
を対合対とする対合 に関して対合であることを示している.
に関して対合であることを示している.
逆に,
 上の点対
上の点対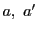 ,
,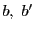 ,
,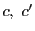 が
同一の対合
が
同一の対合 に関して対合であるとする.
に関して対合であるとする.
 を
を
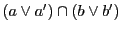 とする.
とする.
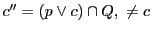 とおくと,
前半より
とおくと,
前半より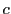 と
と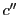 は
は と
と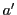 ,
, と
と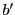 を対合対とする対合に関して対合である.
射影写像は一対一であるから
を対合対とする対合に関して対合である.
射影写像は一対一であるから .よって
.よって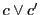 も点
も点 を通る.
□
を通る.
□
注意 4.1.5

を点

に対する対合,点

を対合

の中心,と呼ぶ.
これによって円錐曲線をそれ自身にうつす対合

と,

上にない点

が
一対一に対応していることがわかる.自己対合点は

から

への接線の接点である.
次の命題は1639年,デザルグによって証明された.それが証明1である.
また,1826年にスツルムによって代数的な証明が見出された.それが証明2である.
命題 87
4定点
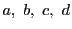
を通る円錐曲線を直線

で切る.
円錐曲線によって定まる二つの交点は,同一の対合で対応している.
■
証明1
2直線
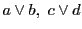 ,
および
,
および
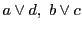 と
と の交点対をそれぞれ
の交点対をそれぞれ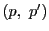 ,
,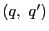 とする.
4定点を通る任意の二次曲線
とする.
4定点を通る任意の二次曲線 をとり,
をとり, との交点対を
との交点対を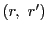 とする.
とする.
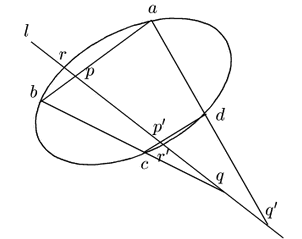 命題85によって
命題85によって
命題76によって
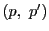 ,
,
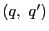 ,
,
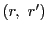 は対合をなす.
は対合をなす.
 を決めれば
を決めれば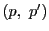 ,
,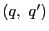 は定点である.
二つの点対によって対合は一意に定まるので,
は定点である.
二つの点対によって対合は一意に定まるので,
 を変えてもやはり同じ対合で点対は対合になる.
□
を変えてもやはり同じ対合で点対は対合になる.
□
この命題の証明の部分に関してその双対命題を掲げる.
先の命題の交点 で直線
で直線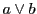 を代表させることにし,
直線
を代表させることにし,
直線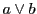 の極も
の極も で表す.
その他も同様にする.
で表す.
その他も同様にする.
系 87.1
4点
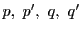
を極とする4極線に接する円錐曲線に,
点

から2接線
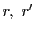
を引く.このとき
が成立し,直線対
が対合をなす.
■
スツルムによる代数的な証明を行うために次の補題を示す.
これは『幾何学大辞典1』[49]で結果のみが記されている.そこでここでその証明をつける.
補題 15
射影直線上に同次座標
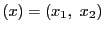
が与えられている.
二つの同次式を
とする.
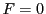
,
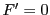
はそれぞれ重根でなく,共通根も待たないとする.
このとき
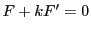
の表す点は,
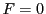
,
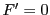
の2組の点対で決まる対合に関して対合である.
その自己対合点は
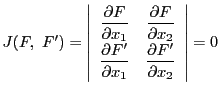
の2根である.
■
証明
 の2根を
の2根を
 ,
,
 の2根を
の2根を
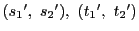 ,
,
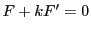 の2根を
の2根を
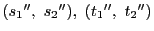 とおく.
また命題72.2によって
とおく.
また命題72.2によって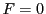 ,
,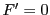 の2組の点対は
対合を定める.これを
の2組の点対は
対合を定める.これを
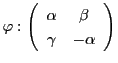 とする.
とする.
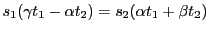 より
より
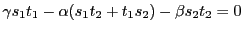 .
.
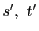 も同様なので,根と係数の関係から
も同様なので,根と係数の関係から
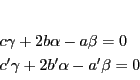 |
(4.2) |
このとき
よって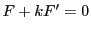 の表す点は,
の表す点は,
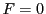 ,
,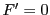 の2組の点対で決まる対合に関して対合である.
の2組の点対で決まる対合に関して対合である.
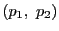 が自己対合点である条件は2次方程式
が自己対合点である条件は2次方程式
を満たすことである.一方,
なので,
等式(4.2)より
である.よって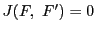 なら
なら
となる.共通根がないので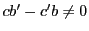 .
よって自己対合点は
.
よって自己対合点は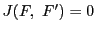 の2根である.
□
の2根である.
□
この補題の下にスツルムによる証明は次のようになされる.
証明2
射影座標を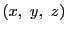 とし,
必要なら射影変換を行い直線
とし,
必要なら射影変換を行い直線 の方程式が
の方程式が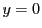 であるとする.
であるとする.
4定点を通る円錐曲線を
とする.円錐曲線は5点を指定すれば一意に定まるので,
同じ4定点を通る円錐曲線の方程式は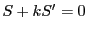 とおける.
とおける.
 とこれらの交点は
とこれらの交点は
で与えられる.この2点は補題15より係数で定まる対合に属する.
□
ベズーの定理の定理は,19世紀,代数幾何を研究した多くの人の手で美しい形に仕上げられた.その原型となった弱い形のベズーの定理は,消去法で導かれる.
今後何度か用いるので,ここで弱い形のベズーの定理を一般的に証明しておこう.
命題 88
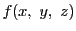
と
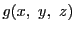
は,
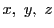
の
次と

次の相異なる既約同次式であるとする.
射影平面上の2曲線
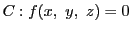 と
と
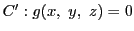 は高々
は高々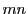 個の共有点をもつ.
■
個の共有点をもつ.
■
証明
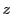 で整理して
で整理して
とおく.
ただし,
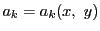 ,
,
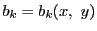 はそれぞれ
はそれぞれ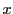 と
と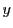 の
の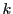 次同次式である.
次同次式である.
ここで必要なら座標変換し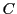 も
も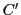 も
も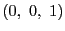 を通らないようにする.
このとき
を通らないようにする.
このとき
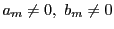 である.
そして
である.
そして
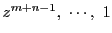 の連立方程式
の連立方程式
を考える.
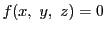 ,
,
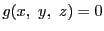 の共通根があるために
の共通根があるために
が必要である.
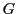 は
は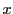 と
と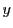 の斉次式となる.その次数を求める.
の斉次式となる.その次数を求める.
一方行列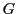 を展開すると,その項は
を展開すると,その項は
一方行列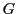 を展開すると,その項は符号を除いて
を展開すると,その項は符号を除いて
と表される.
ただし,
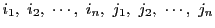 は
は
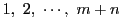 の順列で,
の順列で, については
については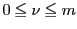 の範囲にないときは0,
の範囲にないときは0,
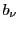 については
については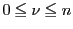 の範囲にないときは0,
とするものとする.
の範囲にないときは0,
とするものとする.
この積が0でないとき,その項の根から見た次数は
したがってその根は多くても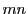 個である.
個である.
その根
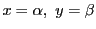 に対し,
に対し,
となる共通根 は一つに定まる.
なぜなら,もし
は一つに定まる.
なぜなら,もし
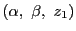 と
と
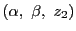 が根であるとする.
この2点を通る直線は
が根であるとする.
この2点を通る直線は を通る.
を通る.
このような組は有限個であるので,座標変換をすることで,
これらの直線が らないようにすることが可能であり,
そのときは,新たな
らないようにすることが可能であり,
そのときは,新たな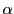 と
と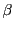 に対して
に対して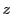 は1個のみ定まる.
は1個のみ定まる.
したがって,共有点の個数は多くても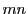 個である.
□
個である.
□
注意 4.1.6
「
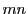
以下」というところを「
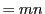
」とするために,
交点数の定義をどのようにするのか,
これが代数幾何を推し進めた一つの動機であった.
交点数の和が二つの曲線の次数の積に一致する,
という型の一般のベズーの定理は,
代数幾何のもっとも基本的な定理である.
注意 4.1.7
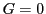
は
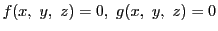
が共通根をもつための
必要条件であった.ベズーの定理はこの必要条件だけで示される.
しかしこれはまた
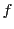
と
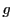
の
終結式に一致し,
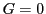
は
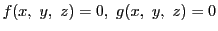
が共通根をもつための
十分条件でもある.
これについては『数学対話』「終結式と不変式」を参照のこと.
二つの円錐曲線の共通点に関する命題を証明するためには,
ベズーの定理を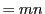 の形で用いなければならない.
そこで,
の形で用いなければならない.
そこで,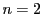 の場合,終結式の理論に立ちかえってこれを示そう.
の場合,終結式の理論に立ちかえってこれを示そう.
補題 16
複素数係数の
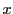
に関する二つの二次方程式
が共通根をもつための必要十分条件は
となることである.
■
証明
とし,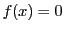 の根を
の根を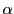 と
と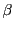 とする.
とする.
なので
これは
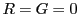 であるとき,
そしてそのときにかぎり
であるとき,
そしてそのときにかぎり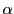 または
または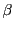 が
が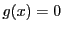 の根となることを示している.
□
の根となることを示している.
□
係数体は複素数体とする.
命題 89
複素数体上の二つの異なる円錐曲線

と
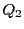
は
重複度を含めて4個の共有点をもつ.
■
証明
円錐曲線 と
と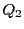 の同次方程式を
の同次方程式を
とする.
ただし
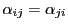 ,
,
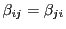 である.ここで必要なら座標を変換し,
これらが
である.ここで必要なら座標を変換し,
これらが
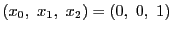 を通らないようにする.
つまり
を通らないようにする.
つまり
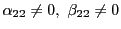 とする.
このとき両式は
とする.
このとき両式は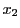 について2次式である.
両式を
について2次式である.
両式を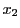 の式とみて補題16を適用する.
の式とみて補題16を適用する.
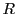 の各係数は
の各係数は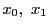 の2次同次式であり,
その結果,
の2次同次式であり,
その結果,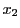 が共有される条件
が共有される条件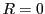 は
は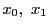 の4次同次方程式となる.
よってその解
の4次同次方程式となる.
よってその解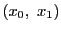 は重複を含めて4個である.
は重複を含めて4個である.
ぞれに対して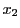 を定める.
もし
を定める.
もし
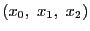 と
と
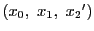 が根であるとする.
この2点を通る直線は
が根であるとする.
この2点を通る直線は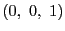 を通る.
を通る.
このような組は有限個であるので,座標変換をすることで,
これらの直線が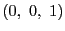 らないようにすることが可能であり,
そのときは,新たな
らないようにすることが可能であり,
そのときは,新たな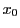 と
と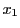 に対して
に対して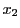 は1個のみ定まる.
は1個のみ定まる.
5個あれば二つの二次曲線は一致するので,
異なる二次曲線は,重複を含めてちょうど4個の共有点をもつ.
□
 の二つの二次曲面
の二つの二次曲面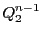 と
と
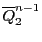 の交わりを通る二次曲面
の交わりを通る二次曲面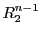 の集合を,
の集合を,
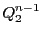 ,
,
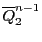 を底とする二次曲面束という.
を底とする二次曲面束という.
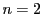 のとき,命題89より
二次曲線
のとき,命題89より
二次曲線 と
と は重複を含めて4点で交わる.
この4点を通る円錐曲線の集合を
は重複を含めて4点で交わる.
この4点を通る円錐曲線の集合を と
と で定まる曲線束という.
で定まる曲線束という.
命題 90
二次曲線

と

の方程式が
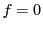
と
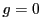
であるとき,
同じ曲線束に属する円錐曲線

の方程式は,
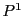
の点
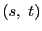
を用いて
と表される.
■
証明
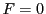 で定まる二次曲線はこの4点を通る.つまり曲線束に属する.
逆に曲線束の二次曲線
で定まる二次曲線はこの4点を通る.つまり曲線束に属する.
逆に曲線束の二次曲線 をとる.その方程式が
をとる.その方程式が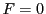 とする.
とする.
 が通る4点以外の点
が通る4点以外の点 をとる.
をとる.
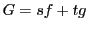 とおき,
とおき,
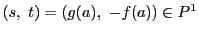 にとれば
にとれば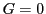 は
は も通る.
5点を通る二次曲線は一意に定まるので,
も通る.
5点を通る二次曲線は一意に定まるので,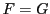 である.
□
である.
□
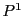 の点
の点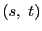 を用いる代わりに,
を用いる代わりに,
 を含めて
を含めて
 とおき,
方程式を
とおき,
方程式を
 としてもよい.
このようにして定まる曲線束の曲線を
としてもよい.
このようにして定まる曲線束の曲線を
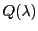 と表す.
特に
と表す.
特に
である.
例 4.1.3
円の束について.
円という概念は射影幾何の概念ではない.
しかし,実のユークリッド空間におかれた円を,
射影空間のなかに入れることはできる.
このとき複素射影平面 おいて「円」とは,
座標を
おいて「円」とは,
座標を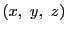 とすると,その方程式が定数
とすると,その方程式が定数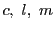 を用いて
を用いて
の形にあらわされるものとなる.
この円は直線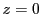 上では
上では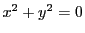 となり,
この結果つねに
となり,
この結果つねに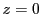 上の2点
上の2点
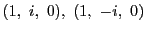 を通る.
を通る.
だから円束は,さらにもう2個の点を指定すれば定まる.
この2点を通る直線が根軸である.
この2点が実平面上にあるか,虚な平面上にあるかで,根軸と交わるかどうかが決まる.
次の命題の厳密な証明は,交点数が必要である.
つまり,二つの円錐曲線の共有点の型がこれですべてであることを示すためには,
ベズーの定理の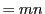 の形のものが必要で,そのベズーの定理では,
ありうる交点数をすべて書き出すことができる.
しかし,その証明はここでは行わない.
代数幾何の教科書か,または『Poncelet's Theorem』[40]などを参照してもらいたい.
の形のものが必要で,そのベズーの定理では,
ありうる交点数をすべて書き出すことができる.
しかし,その証明はここでは行わない.
代数幾何の教科書か,または『Poncelet's Theorem』[40]などを参照してもらいたい.
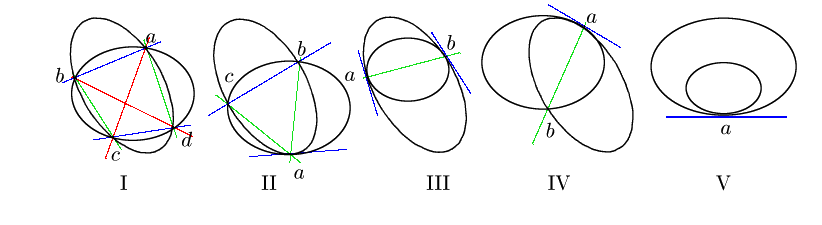
命題 91

と

を異なる円錐曲線とし,その行列を
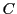
,
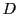
とする.
また
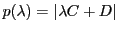
とおく.
これは
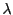
の3次式である.
4の分割
に応じて,

と

の共有点とそこでの重複度は次のようになる.
さらに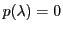 の根
の根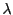 はこれらの共有点を通る直線に分解する退化二次曲線を定める.
はこれらの共有点を通る直線に分解する退化二次曲線を定める.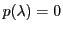 の根は
異なる3根,重根と単根が一つずつ,3重根の場合がある.
添え字が異なるものは異なる根とする.
それらをまとめると表,および図のようになる.
ここで
の根は
異なる3根,重根と単根が一つずつ,3重根の場合がある.
添え字が異なるものは異なる根とする.
それらをまとめると表,および図のようになる.
ここで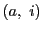 は共有点
は共有点 とそこでの重複度を表す.
また
とそこでの重複度を表す.
また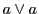 は
は での接線を表す.
での接線を表す.
■
 と
と が異なる4点を共有するとき,
この2つの円錐曲線は一般の位置にあるという.
が異なる4点を共有するとき,
この2つの円錐曲線は一般の位置にあるという.
系 91.1

と

を異なる円錐曲線とし,その行列を
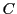
,
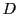
とする.

と

が一般の位置にある必要十分条件は,
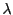
の3次方程式
が相異なる3根をもつことである.
■
命題 92
円錐曲線

と

上にない点

に対し,2点
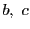
で,

と
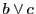
,

と
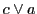
,
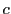
と
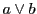
がそれぞれ

に関する極と極線であるものが存在する.
■
証明
 を定める行列を
を定める行列を としその方程式を
としその方程式を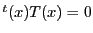 ,
点
,
点 の座標を
の座標を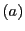 とする,
直線
とする,
直線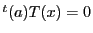 上の点
上の点 をとる.
2直線
をとる.
2直線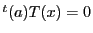 ,
,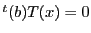 の交点を
の交点を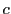 とする.
とする.
 と
と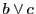 ,
, と
と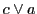 は極と極線である.
は極と極線である.
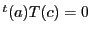 ,
,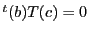 なので
なので
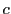 の極線
の極線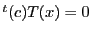 は
は と
と を通る.
よって
を通る.
よって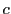 と
と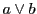 も極と極線であり,この
も極と極線であり,この ,
,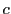 が条件を満たす.
□
が条件を満たす.
□
三角形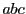 を円錐曲線
を円錐曲線 の極三角形という.
の極三角形という.
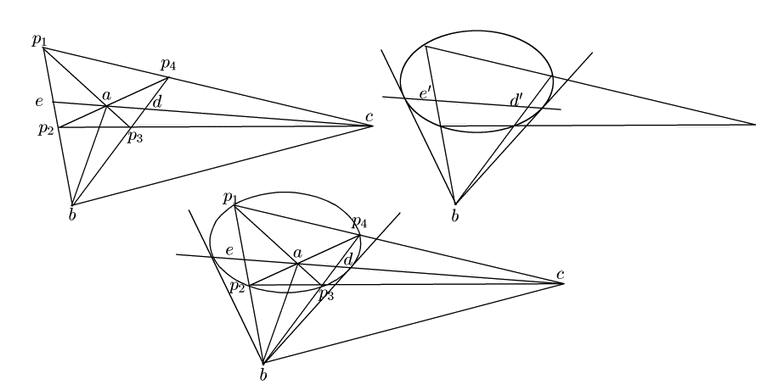
命題 93
完全四角形
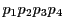
の各頂点を通る円錐曲線

がある.
対角線の交点を
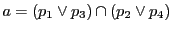
,
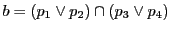
,
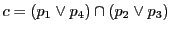
とする.
このとき三角形
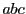
は円錐曲線

の極三角形である.
逆に円錐曲線 と極三角形が与えられれば,4頂点が
と極三角形が与えられれば,4頂点が 上にあり,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
上にあり,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
証明
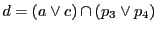 ,
,
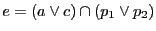 とおく.
命題70の系70.1より
とおく.
命題70の系70.1より
![$[p_4,\ p_3;\ d,\ b]=[b,\ d;\ p_3,\ p_4]=-1$](images/img2359.gif) .
一方,点
.
一方,点 の極線と
の極線と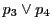 との交点を
との交点を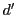 ,
,
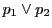 との交点を
との交点を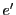 とする.
命題85より
とする.
命題85より
![$[b,\ d';\ p_3,\ p_4]=-1$](images/img2361.gif) .
この結果
.
この結果 .同様に
.同様に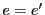 となり,点
となり,点 の極線が
の極線が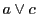 である.
他も同様である.
よって三角形
である.
他も同様である.
よって三角形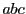 は円錐曲線
は円錐曲線 の極三角形である.
の極三角形である.
逆に,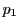 を
を 上にとればそれに対して他の3点が確定し完全四角形で条件を満たすものが得られる.
□
上にとればそれに対して他の3点が確定し完全四角形で条件を満たすものが得られる.
□
系 93.1
完全四角形
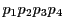
の各辺に接する円錐曲線

がある.
対角線の交点を
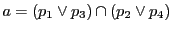
,
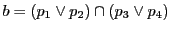
,
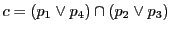
とする.
このとき三角形
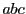
は円錐曲線

の極三角形である.
逆に円錐曲線 と極三角形が与えられれば,4辺が
と極三角形が与えられれば,4辺が に接し,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
に接し,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
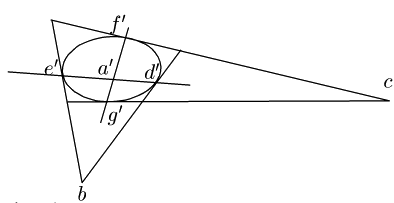 証明
完全四角形に関する記号は命題のままとし,
接点を図のように
証明
完全四角形に関する記号は命題のままとし,
接点を図のように
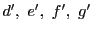 とおく.
また
とおく.
また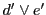 と
と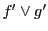 の交点を
の交点を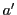 とする.
とする.
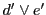 は
は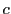 を,
を,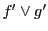 は
は を通る.
を通る.
複比を考えることによって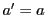 .
これから
.
これから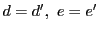 が成立するので,
同じ論理で系が成立する.
□
が成立するので,
同じ論理で系が成立する.
□
命題93をもとに1850年のシルベスターの定理が成り立つ.
命題 94
異なる4点で交わる二つの円錐曲線

,
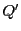
はある極三角形を共有する.
■
証明
4点は一般の位置にある.この4点による完全四角形を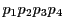 とすれば,命題93の三角形
とすれば,命題93の三角形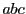 が
が と
と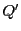 に共有される.
□
に共有される.
□
注意 4.1.8
サーモンの『解析幾何学(円錐曲線)』[
35]第282款(437頁)では
「任意の二つの円錐曲線は、常に一つの自共役三角形(極三角形のこと)を共有する」とあり,
岩田至康(編)の『幾何学大辞典6』[
46]619命題(299頁)では
「2つの円錐曲線はつねに1つの極三角形を共有する」とある.
異なる4点では交わらない場合は一般には成立しない.
命題 95
相異なる4点で交わる二つの円錐曲線

,
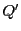
は,
適当な枠をとることによって,その方程式を
の形にすることができる.
■
証明
二つの円錐曲線 ,
,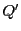 が共有する極三角形
が共有する極三角形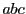 の3頂点を基本点にとる.
の3頂点を基本点にとる.
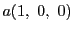 ,
,
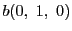 ,
,
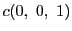 とする.
とする.
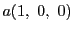 の極線が
の極線が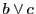 つまり
つまり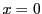 であることなどより,
このときそれぞれの対称行列
であることなどより,
このときそれぞれの対称行列 と
と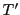 の対角成分以外の成分は0である.
単位点を適当にとることによって,一方の側の3係数を1にすることができる.
□
の対角成分以外の成分は0である.
単位点を適当にとることによって,一方の側の3係数を1にすることができる.
□
逆にこの形に表される円錐曲線は,
3点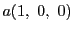 ,
,
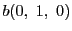 ,
,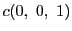 とするとき,三角形
とするとき,三角形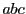 がこの円錐曲線の極三角形である.
がこの円錐曲線の極三角形である.


 次: パスカルの定理
上: 二次曲面の定義
前: 諸定義とその関係
2014-01-03
次: パスカルの定理
上: 二次曲面の定義
前: 諸定義とその関係
2014-01-03
 1)
1)
![]() がすべて異なるとき.
がすべて異なるとき.
![]() 上にこれら4点と異なる
上にこれら4点と異なる![]() をとる.図のように交点
をとる.図のように交点
![]() をとる.
をとる.
![]() の定義から
の定義から
![\begin{eqnarray*}
&&[o,\ q;\ m,\ p]=[n,\ r;\ o',\ p]\\
&∴&[a\vee o,\ a\vee ...
...a\vee m,\ a\vee p]=[a'\vee n,\ a'\vee r;\ a'\vee o',\ a'\vee p]
\end{eqnarray*}](images/img2168.gif)
![]() と異なる2点
と異なる2点![]() をとれば,
をとれば,
![]() と
と![]() は射影的.これを改めて母線束にとれば
は射影的.これを改めて母線束にとれば![]() と
と![]() は射影的である. □
は射影的である. □
![]() から
4直線
から
4直線
![]() への射影写像
への射影写像![]() が存在する.
定義26から,
複比
が存在する.
定義26から,
複比
![]() は双対空間の直線上の4点の複比として定まっているが,
は双対空間の直線上の4点の複比として定まっているが,
![]() は双対空間の射影写像を引き起こし,
複比は射影写像で不変であるから,
複比
は双対空間の射影写像を引き起こし,
複比は射影写像で不変であるから,
複比
![]() は点
は点![]() のとり方によらない.
□
のとり方によらない.
□
![\begin{eqnarray*}
&&[b,\ c;\ m,\ n]=[a'\vee b,\ a'\vee c;\ a'\vee m,\ a'\vee n]...
...m',\ a\vee n';\ a\vee b',\ a\vee c']\\
&=&[m',\ n';\ b',\ c']
\end{eqnarray*}](images/img2190.gif)
 いいかえると点
いいかえると点![]() を中心とする線束から
点
を中心とする線束から
点![]() を中心とする線束への射影写像が存在する.
これがもし背景的であるとすると,点
を中心とする線束への射影写像が存在する.
これがもし背景的であるとすると,点![]() は背景写像でそれ自身に対応する.
つまり点
は背景写像でそれ自身に対応する.
つまり点![]() は円錐曲線
は円錐曲線![]() 上になければならない.
これは
上になければならない.
これは
![]() が異なるという仮定に反する.
が異なるという仮定に反する.![]() ,直線
,直線![]() と
その上の点
と
その上の点![]() ,
,
![]() は,
双対空間で2点とそれらの点を中心とする線束となり,
かつその線束の間の射影写像が存在したので,
ある二次曲線を定める.
は,
双対空間で2点とそれらの点を中心とする線束となり,
かつその線束の間の射影写像が存在したので,
ある二次曲線を定める.
![]() のある平面に戻ると,それらはある二次曲線の接線となっている.
つまりこれら三角形の辺に内接する円錐曲線
のある平面に戻ると,それらはある二次曲線の接線となっている.
つまりこれら三角形の辺に内接する円錐曲線![]() が存在する.
□
が存在する.
□
![]() が複素数体の場合,直線は
が複素数体の場合,直線は![]() と2点で交わるか,
交点を求める方程式が重解,つまり接するかのいずれかである.
と2点で交わるか,
交点を求める方程式が重解,つまり接するかのいずれかである.
![]() と
と![]() の対応において,
点に対しては極線が,直線に対しては極点が対応し,
極系によって定まる正則二次曲線上の点に対しては,その接線の集合が対応する.
の対応において,
点に対しては極線が,直線に対しては極点が対応し,
極系によって定まる正則二次曲線上の点に対しては,その接線の集合が対応する.
![]() の他の二次曲線は,その上の点に対する極線の集合が対応し,
正則であればそれは二次曲線の包絡線となっている.
の他の二次曲線は,その上の点に対する極線の集合が対応し,
正則であればそれは二次曲線の包絡線となっている.
![]() における2直線であれば,それは
における2直線であれば,それは![]() の2点とそこを通る直線の集合が対応する.
の2点とそこを通る直線の集合が対応する.
![]() がある.
がある.![]() 上にない点
上にない点![]() の極線を
の極線を![]() とし,
とし,
![]() を通る任意の直線が
を通る任意の直線が![]() および
および![]() と交わる点を
と交わる点を![]() ,
,![]() とする.
とする.
![]() は
は![]() を調和に分ける.
■
を調和に分ける.
■
 証明
点
証明
点![\begin{eqnarray*}
&&[p,\ q;\ a,\ b]
=[c\vee p,\ c\vee q;\ c\vee a,\ c\vee b]\\
&=&[c\vee c,\ c\vee d;\ c\vee a,\ c\vee b]
\end{eqnarray*}](images/img2206.gif)
![\begin{eqnarray*}
&&[c\vee c,\ c\vee d;\ c\vee a,\ c\vee b]
=[d\vee c,\ d\vee ...
...
&=&[d\vee q,\ d\vee p;\ d\vee a,\ d\vee b]
=[q,\ p;\ a,\ b]
\end{eqnarray*}](images/img2208.gif)
 証明
図のように点
証明
図のように点![]() を通る任意の3線
を通る任意の3線![]() をとり,
をとり,![]() と
と![]() を固定し,
を固定し,
![]() を動線と考える.これらの直線と
を動線と考える.これらの直線と![]() の共有点を
の共有点を![]() ,
,![]() ,
,![]() とする.
とする.
![]() とおく.
とおく.![\begin{eqnarray*}
&&[a,\ a';\ b,\ c]\\
&=&[b'\vee a,\ b'\vee a';\ b'\vee b,\ ...
...e a',\ c\vee a;\ c\vee b',\ c\vee c']\\
&=&[a',\ a;\ b',\ c']
\end{eqnarray*}](images/img2227.gif)
![]() と
と![]() が,
が,
![]() と
と![]() ,
,![]() と
と![]() を対合対とする対合
を対合対とする対合![]() に関して対合であることを示している.
に関して対合であることを示している.
![]() 上の点対
上の点対![]() ,
,![]() ,
,![]() が
同一の対合
が
同一の対合![]() に関して対合であるとする.
に関して対合であるとする.
![]() を
を
![]() とする.
とする.
![]() とおくと,
前半より
とおくと,
前半より![]() と
と![]() は
は![]() と
と![]() ,
,![]() と
と![]() を対合対とする対合に関して対合である.
射影写像は一対一であるから
を対合対とする対合に関して対合である.
射影写像は一対一であるから![]() .よって
.よって![]() も点
も点![]() を通る.
□
を通る.
□
 命題85によって
命題85によって
![\begin{eqnarray*}
&&[p,\ q;\ r,\ r']=[b\vee p,\ b\vee q;\ b\vee r,\ b\vee r']\\...
...=&[d\vee c,\ d\vee a;\ d\vee r',\ d\vee r]
=[p',\ q';\ r',\ r]
\end{eqnarray*}](images/img2241.gif)
![]() ,
,
![]() ,
,
![]() は対合をなす.
は対合をなす.
![]() を決めれば
を決めれば![]() ,
,![]() は定点である.
二つの点対によって対合は一意に定まるので,
は定点である.
二つの点対によって対合は一意に定まるので,
![]() を変えてもやはり同じ対合で点対は対合になる.
□
を変えてもやはり同じ対合で点対は対合になる.
□
![]() で直線
で直線![]() を代表させることにし,
直線
を代表させることにし,
直線![]() の極も
の極も![]() で表す.
その他も同様にする.
で表す.
その他も同様にする.
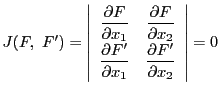 の2根である.
■
の2根である.
■
 とする.
とする.
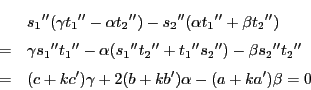
![]() が自己対合点である条件は2次方程式
が自己対合点である条件は2次方程式
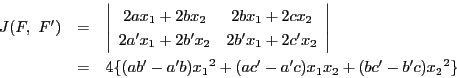
![]() とし,
必要なら射影変換を行い直線
とし,
必要なら射影変換を行い直線![]() の方程式が
の方程式が![]() であるとする.
であるとする.
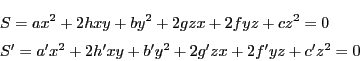
![]() とこれらの交点は
とこれらの交点は
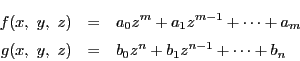
![]() も
も![]() も
も![]() を通らないようにする.
このとき
を通らないようにする.
このとき
![]() である.
そして
である.
そして
![]() の連立方程式
の連立方程式
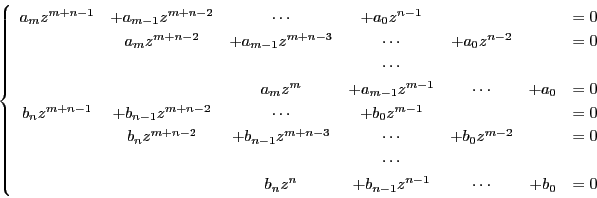
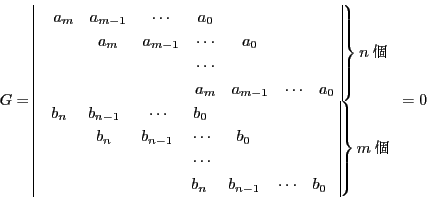
![]() は
は![]() と
と![]() の斉次式となる.その次数を求める.
の斉次式となる.その次数を求める.
![]() を展開すると,その項は
を展開すると,その項は
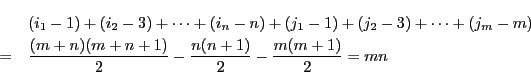
![]() に対し,
に対し,
![]() らないようにすることが可能であり,
そのときは,新たな
らないようにすることが可能であり,
そのときは,新たな![]() と
と![]() に対して
に対して![]() は1個のみ定まる.
は1個のみ定まる.
![]() 個である.
□
個である.
□
![]() を定める.
もし
を定める.
もし
![]() と
と
![]() が根であるとする.
この2点を通る直線は
が根であるとする.
この2点を通る直線は![]() を通る.
を通る.
![]() らないようにすることが可能であり,
そのときは,新たな
らないようにすることが可能であり,
そのときは,新たな![]() と
と![]() に対して
に対して![]() は1個のみ定まる.
は1個のみ定まる.
![]() のとき,命題89より
二次曲線
のとき,命題89より
二次曲線![]() と
と![]() は重複を含めて4点で交わる.
この4点を通る円錐曲線の集合を
は重複を含めて4点で交わる.
この4点を通る円錐曲線の集合を![]() と
と![]() で定まる曲線束という.
で定まる曲線束という.
![]() の点
の点![]() を用いる代わりに,
を用いる代わりに,
![]() を含めて
を含めて
![]() とおき,
方程式を
とおき,
方程式を
![]() としてもよい.
このようにして定まる曲線束の曲線を
としてもよい.
このようにして定まる曲線束の曲線を
![]() と表す.
特に
と表す.
特に
![]() おいて「円」とは,
座標を
おいて「円」とは,
座標を![]() とすると,その方程式が定数
とすると,その方程式が定数![]() を用いて
を用いて
![]() 上では
上では![]() となり,
この結果つねに
となり,
この結果つねに![]() 上の2点
上の2点
![]() を通る.
を通る.
![]() の根
の根![]() はこれらの共有点を通る直線に分解する退化二次曲線を定める.
はこれらの共有点を通る直線に分解する退化二次曲線を定める.![]() の根は
異なる3根,重根と単根が一つずつ,3重根の場合がある.
添え字が異なるものは異なる根とする.
それらをまとめると表,および図のようになる.
ここで
の根は
異なる3根,重根と単根が一つずつ,3重根の場合がある.
添え字が異なるものは異なる根とする.
それらをまとめると表,および図のようになる.
ここで![]() は共有点
は共有点![]() とそこでの重複度を表す.
また
とそこでの重複度を表す.
また![]() は
は![]() での接線を表す.
での接線を表す.

![]() と
と![]() が異なる4点を共有するとき,
この2つの円錐曲線は一般の位置にあるという.
が異なる4点を共有するとき,
この2つの円錐曲線は一般の位置にあるという.
![]() を円錐曲線
を円錐曲線![]() の極三角形という.
の極三角形という.
![]() と極三角形が与えられれば,4頂点が
と極三角形が与えられれば,4頂点が![]() 上にあり,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
上にあり,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
![]() を
を![]() 上にとればそれに対して他の3点が確定し完全四角形で条件を満たすものが得られる.
□
上にとればそれに対して他の3点が確定し完全四角形で条件を満たすものが得られる.
□
![]() と極三角形が与えられれば,4辺が
と極三角形が与えられれば,4辺が![]() に接し,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■
に接し,対辺の交点がその極三角形の3頂点となる完全四角形がある.
■ 証明
完全四角形に関する記号は命題のままとし,
接点を図のように
証明
完全四角形に関する記号は命題のままとし,
接点を図のように
![]() とおく.
また
とおく.
また![]() と
と![]() の交点を
の交点を![]() とする.
とする.
![]() は
は![]() を,
を,![]() は
は![]() を通る.
を通る.![]() .
これから
.
これから![]() が成立するので,
同じ論理で系が成立する.
□
が成立するので,
同じ論理で系が成立する.
□![]() ,
,
![]() ,
,![]() とするとき,三角形
とするとき,三角形![]() がこの円錐曲線の極三角形である.
がこの円錐曲線の極三角形である.