

 次: 楕円積分による証明
上: ポンスレの定理
前: 線型代数による証明
次: 楕円積分による証明
上: ポンスレの定理
前: 線型代数による証明
ポンスレの閉形定理11自体を,フルビッツによる対応原理で証明しよう.
複素数体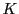 上の
上の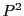 におかれた二次曲線
におかれた二次曲線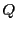 は適当な射影変換によって
は適当な射影変換によって
という標準形になり,それらは二次式による媒介変数表示
をもつ.
つまり二次曲線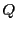 上の点
上の点 は
は
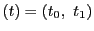 という
という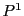 に値をもつ媒介変数を用いて
に値をもつ媒介変数を用いて
と表される.
補題 19
二つの二次曲線
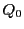
と
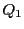
がある.
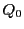
上の2点
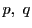
が
それぞれ媒介変数
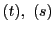
を用いて表されているとする.
直線
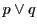
が
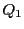
に接するための必要十分条件は,
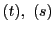
のそれぞれに関する二次の等式で表される.
証明
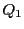 を定める対称行列を
を定める対称行列を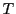 とする.
とする.
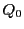 上の動点
上の動点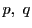 が
それぞれ二次式
が
それぞれ二次式
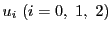 によって
によって
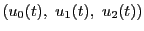 ,
,
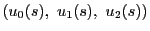 と表されるとする.
よって直線
と表されるとする.
よって直線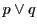 は
は
となる.これは
とも書ける.
一方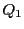 上の点
上の点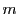 での接線は
での接線は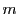 の座標も
の座標も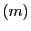 とすれば
とすれば
と表される.これが直線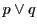 と一致するので,
ただし定数倍の同値類で考えることにより
と一致するので,
ただし定数倍の同値類で考えることにより
である.つまり
この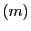 は
は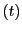 と
と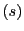 のそれぞれについて一次式である.
この
のそれぞれについて一次式である.
この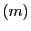 が
が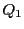 上に存在することが,
上に存在することが,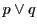 が
が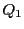 に接することを意味する.
に接することを意味する.
この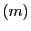 を
を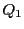 の方程式
の方程式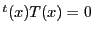 に代入すると,
確かに
に代入すると,
確かに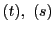 のそれぞれに関する二次の等式になっている.
□
のそれぞれに関する二次の等式になっている.
□
この双二次式を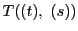 と表す.
またこの式を
と表す.
またこの式を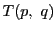 とも表す.
とも表す.
補題 20
平面上に二つの二次曲線
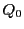
と
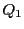
がある.
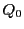
上の点
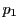
から
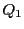
にひとつの接線をひき,
その延長が再び
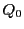
と交わる点を
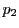
とする.
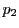
から
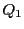
に
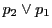
とは異なる接線をひき,
その延長が再び
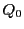
と交わる点を
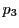
とする.
このようにして点
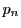
を定める.
点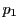 が媒介変数
が媒介変数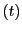 で表され,
点
で表され,
点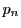 が媒介変数
が媒介変数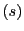 で表されるとすると
で表されるとすると
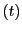 と
と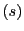 の間には,それぞれについて二次の関係式
の間には,それぞれについて二次の関係式
が成立する.
証明
数学的帰納法で示す.
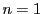 のとき.
のとき.
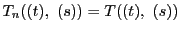 なので成立する.
なので成立する.
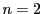 のとき.
のとき.
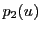 として,連立方程式
として,連立方程式
から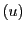 を消去する.補題16によって,
を消去する.補題16によって,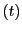 と
と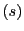 のそれぞれに関して4次の関係式が得られる.
のそれぞれに関して4次の関係式が得られる.
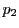 は2個とれて,その各々から
は2個とれて,その各々から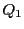 には
には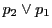 ともう一つの接線が引ける.
よってこの関係式は
ともう一つの接線が引ける.
よってこの関係式は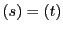 を重根にもつ.
その部分はは
を重根にもつ.
その部分はは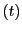 と
と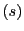 のそれぞれに関する二次式である.
この関係式をこの二次式で約分して,商を
のそれぞれに関する二次式である.
この関係式をこの二次式で約分して,商を
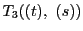 とすれば.
とすれば.
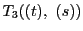 は
は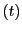 と
と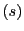 のそれぞれに関して二次式で,
のそれぞれに関して二次式で,
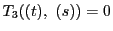 の2根が
の2根が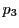 を与える.
を与える.
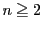 に対して
に対して
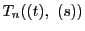 が定まったとする.
連立方程式
が定まったとする.
連立方程式
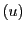 を消去する.補題16によって,
を消去する.補題16によって,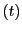 と
と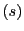 のそれぞれに関して四次の関係式が得られる.
この4次式は
のそれぞれに関して四次の関係式が得られる.
この4次式は
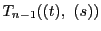 を因数にもつ.
それで約した式を
を因数にもつ.
それで約した式を
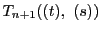 とすれば
とすれば
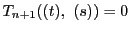 がなりたつ.
数学的帰納法によって証明が終わった.
□
がなりたつ.
数学的帰納法によって証明が終わった.
□
これを用いてポンスレの閉形定理を単純な形で証明しよう.
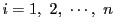 に対し
点
に対し
点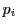 が媒介変数
が媒介変数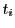 で表されるとする.
で表されるとする.
一般に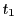 と
と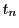 の間には,それぞれについて2次の関係式
の間には,それぞれについて2次の関係式
が成立する.
点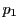 が
が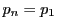 を満たすことは,
を満たすことは,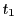 が
が
を満たすことと同値である.これが他の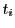 についても成立する.
についても成立する.
さらに,
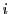 を1から
を1から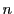 のいずれかとして
のいずれかとして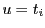 とする.
とする.
は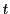 の2次方程式で
の2次方程式で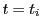 は重根である.
は重根である.
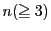 に対して4次方程式
に対して4次方程式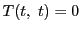 は重複度も含めて
は重複度も含めて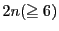 個の
根をもつ.よって等式
個の
根をもつ.よって等式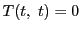 は恒等式であり,
任意の
は恒等式であり,
任意の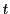 に対して成立する.
つまり
に対して成立する.
つまり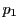 を任意にとり,順次
を任意にとり,順次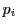 を定めるとき,
を定めるとき,
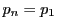 となる.
□
となる.
□


 次: 楕円積分による証明
上: ポンスレの定理
前: 線型代数による証明
2014-01-03
次: 楕円積分による証明
上: ポンスレの定理
前: 線型代数による証明
2014-01-03
![]() 上の
上の![]() におかれた二次曲線
におかれた二次曲線![]() は適当な射影変換によって
は適当な射影変換によって
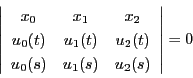
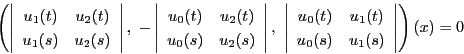
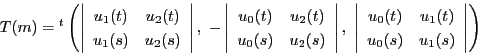
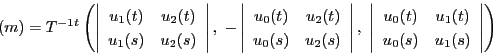
![]() を
を![]() の方程式
の方程式![]() に代入すると,
確かに
に代入すると,
確かに![]() のそれぞれに関する二次の等式になっている.
□
のそれぞれに関する二次の等式になっている.
□
![]() と表す.
またこの式を
と表す.
またこの式を![]() とも表す.
とも表す.
![]() が媒介変数
が媒介変数![]() で表され,
点
で表され,
点![]() が媒介変数
が媒介変数![]() で表されるとすると
で表されるとすると
![]() と
と![]() の間には,それぞれについて二次の関係式
の間には,それぞれについて二次の関係式
![]() のとき.
のとき.
![]() なので成立する.
なので成立する.
![]() のとき.
のとき.
![]() として,連立方程式
として,連立方程式
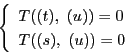
![]() は2個とれて,その各々から
は2個とれて,その各々から![]() には
には![]() ともう一つの接線が引ける.
よってこの関係式は
ともう一つの接線が引ける.
よってこの関係式は![]() を重根にもつ.
その部分はは
を重根にもつ.
その部分はは![]() と
と![]() のそれぞれに関する二次式である.
この関係式をこの二次式で約分して,商を
のそれぞれに関する二次式である.
この関係式をこの二次式で約分して,商を
![]() とすれば.
とすれば.
![]() は
は![]() と
と![]() のそれぞれに関して二次式で,
のそれぞれに関して二次式で,
![]() の2根が
の2根が![]() を与える.
を与える.
![]() に対して
に対して
![]() が定まったとする.
連立方程式
が定まったとする.
連立方程式
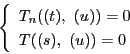
![]() と
と![]() の間には,それぞれについて2次の関係式
の間には,それぞれについて2次の関係式
![]() を1から
を1から![]() のいずれかとして
のいずれかとして![]() とする.
とする.
![]() に対して4次方程式
に対して4次方程式![]() は重複度も含めて
は重複度も含めて![]() 個の
根をもつ.よって等式
個の
根をもつ.よって等式![]() は恒等式であり,
任意の
は恒等式であり,
任意の![]() に対して成立する.
つまり
に対して成立する.
つまり![]() を任意にとり,順次
を任意にとり,順次![]() を定めるとき,
を定めるとき,
![]() となる.
□
となる.
□