

 次: むすび
上: 代数幾何へ
前: 楕円関数による証明
次: むすび
上: 代数幾何へ
前: 楕円関数による証明
 に内接し,
に内接し, に外接する
に外接する 角形を
ポンスレ
角形を
ポンスレ 角形といおう.
以下,ポンスレ
角形といおう.
以下,ポンスレ 角形を考えるときは
角形を考えるときは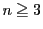 とする.
とする.
 と
と がどのような条件を満たせば
ポンスレ
がどのような条件を満たせば
ポンスレ 角形が存在するのか.
角形が存在するのか.
ケーリーはこれにも答えている.
しかしケーリーは結果のみを書いている.
論文集第2巻[42]所収の第115論文の結果を第116論文で訂正している.
おそらくケーリーは膨大な計算のなかから帰納的に結論を得たのだろう.
そしてその証明は,あるいはケーリーにとっては余りに自明なことであったのかも知れない.
その結果に対して,1978年グリヒス(Griffiths) と ハリス(Harris)が代数幾何的な
証明をおこなった.
それが『ON CAYLEY'S EXPLICIT SOLUTION TO PONCELET'S PORISM』[39]
である.グリヒスとハリスは,「このような十分条件を当初は知らなかった.
この結論をケーリーは煩雑な楕円関数の考察から得たのかも知れない.
しかしいずれにせよあまりにも結論は簡明である.
この結論に対して代数幾何的な証明ができる」とのべ,それを実行している.
19世紀中葉,複素函数論にはじまり楕円関数からさらにその先へと,
リーマン,アーベル,ヤコビ,そしてガウスらによって解析的な代数幾何がきり拓かれ,
大きく展開した.それは代数,幾何,解析の交叉する古典数学の華であった.
同じ頃,ポンスレらによる射影幾何もまた大きく発展した.
ポンスレの定理からケーリーのポンスレ条件の発見もまた,この時代のことであった.
ヤコビ,ケーリーの仕事にその結びつきの端緒があった.
1970年代になって,この二つが深く結びつき,
ポンスレ条件の代数幾何による証明がなされたのである.
ここでその基本的な論の構成を行う.
ここでは証明をつけることを主眼にするのではなく.
逆に根拠をたどる方向で構成する.
証明や演繹的な構成は参考文献『Poncelet's Theorem』[40],
『Poncelet Porisms and Beyond』[41]などを見てもらいたい.
 にある円錐曲線
にある円錐曲線 の接線は双対空間
の接線は双対空間 の点である.
円錐曲線
の点である.
円錐曲線 の接線の集合は双対空間
の接線の集合は双対空間 の曲線をなす.
この曲線を
の曲線をなす.
この曲線を の双対曲線といい
の双対曲線といい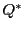 と表す.
と表す.
命題 107
円錐曲線

を定める行列を

とする.
このとき
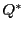
は
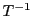
で定まる

の円錐曲線である.
■
証明
 の座標を
の座標を
 ,
,
 の座標を
の座標を
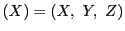 とする.
とする.
 の方程式を
の方程式を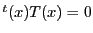 とする.
とする.
 上の点
上の点
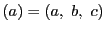 での接線は
での接線は
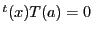 である.
この接線は
である.
この接線は の点
の点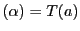 に対応する.
よって
に対応する.
よって
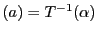 であり,
であり, は対称なので
は対称なので
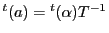 である.
である.
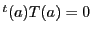 なので,
なので,
つまり,点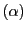 は方程式
は方程式
を満たす.逆も成り立つ.よってこれが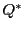 の方程式である.
□
の方程式である.
□
系 107.1
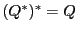
である.■
明らかである.
命題 108

と

が一般の位置にあるとする.
このとき,
行列式
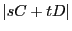
によって定まる曲線
は,楕円曲線である.これを
線束楕円曲線という.
証明
一般に,射影平面上の曲線で
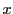 の3次または4次式
の3次または4次式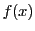 を用いて非斉次座標で
を用いて非斉次座標で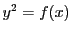 で表され,特異点をもたない曲線と曲線上の指定された点(単位点)の組を楕円曲線という.
で表され,特異点をもたない曲線と曲線上の指定された点(単位点)の組を楕円曲線という.
複素数体上の射影幾何であるので,
射影変換によって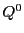 と
と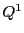 の方程式を
の方程式を
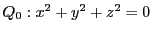 ,
,
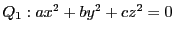 として一般性を失わない.
として一般性を失わない.
この射影変換によって,変数の定数倍することで
曲線
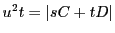 は
は
となる.
二つの二次曲線 と
と が一般の位置にあれば,
が一般の位置にあれば,
 ,
, ,
,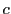 は相異なり,
ワイエルシュトラスの
は相異なり,
ワイエルシュトラスの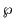 関数
といわれる非特異な楕円曲線である.
□
関数
といわれる非特異な楕円曲線である.
□
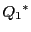 の点は
の点は の直線に対応する.
の直線に対応する. の点と
の点と の直線を同一視する.
2つの円錐曲線の直積集合
の直線を同一視する.
2つの円錐曲線の直積集合
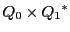 の部分集合
の部分集合 を次のように定める.
を次のように定める.
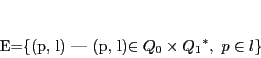 |
(5.20) |
次の事実が成り立つ.
命題 109

は

と

で定まる線束楕円曲線と双有理同型な
楕円曲線である.
これをポンスレ対応曲線という.
■
証明
複素数体上の射影幾何であるので,
射影変換によって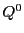 と
と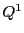 の方程式を
の方程式を
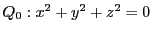 ,
,
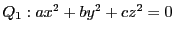 として一般性を失わない.
このとき楕円曲線
として一般性を失わない.
このとき楕円曲線 は方程式
は方程式
で定まる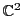 におかれた楕円曲線と双有理同型であることを示す.
におかれた楕円曲線と双有理同型であることを示す.
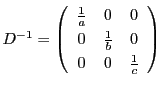 であるから
であるから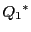 は方程式
は方程式
で定まる円錐曲線である.
よって集合 は
は
と表される.
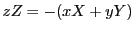 より
より
これから
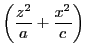 をかけて平方完成して
をかけて平方完成して
を得る.以下計算を簡明にするため非同次座標で考える.
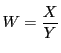 とする.
とする.
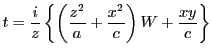 とおく.
とおく.
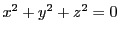 は
は
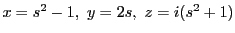 という媒介変数表示をもつので,
という媒介変数表示をもつので,
つまり適当な平方根をとって
を得る.ここで
と置き換えると
これから
となる.
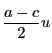 を
を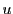 ,
,
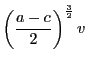 を
を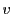 にとり直すことによって
にとり直すことによって
最後に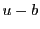 を
を にとり直して.
にとり直して.
を得る.
ところが
である.
 と
と が一般の位置にある場合,
が一般の位置にある場合,
 ,
, ,
,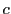 は相異なり,
その結果,
は相異なり,
その結果,
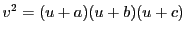 は非特異な楕円曲線である.
□
は非特異な楕円曲線である.
□
以上は,『代数幾何学』[38]による代数的な計算にもとづく証明である.
この証明はまた,『Poncelet's Theorem』[40]にあるように,
 に解析構造を入れ,リーマン面としこれが楕円曲線であることを示す,
という方向でもなされる.これは後におこなう.
に解析構造を入れ,リーマン面としこれが楕円曲線であることを示す,
という方向でもなされる.これは後におこなう.
以下,楕円曲線の点の間の和と差は加群としての演算である.
接線 と
と との他の交点を
との他の交点を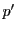 とする.これによって
写像
とする.これによって
写像
が定まる.点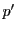 を通り
を通り に接する他の接線を
に接する他の接線を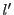 とする.これによって
写像
とする.これによって
写像
が定まる.これらはそれぞれ 上の対合である.
その合成をとり
上の対合である.
その合成をとり
とおく.
これを用いると,
ポンスレの定理は次のように表される.
命題 110
自然数

に対して,
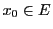
で
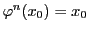
となるものが存在すれば,
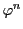
は

の恒等写像である.
■
このようにとらえることで,
ポンスレの定理を とその上の対合の合成に関する命題としてとらえることができる.
この命題そのものは,われわれもさまざまの方法で証明してきた.
さらに次に示すような代数群としての
とその上の対合の合成に関する命題としてとらえることができる.
この命題そのものは,われわれもさまざまの方法で証明してきた.
さらに次に示すような代数群としての の演算を用いる証明が出来る.
の演算を用いる証明が出来る.
どのような条件を と
と が満たせば,
ポンスレ
が満たせば,
ポンスレ 角形が存在するのか.
ポンスレ
角形が存在するのか.
ポンスレ 角形の存在条件をポンスレ条件といおう.
角形の存在条件をポンスレ条件といおう.
 ここでケーリーからグリヒスに引き継がれた考え方を用いる.
ここでケーリーからグリヒスに引き継がれた考え方を用いる.
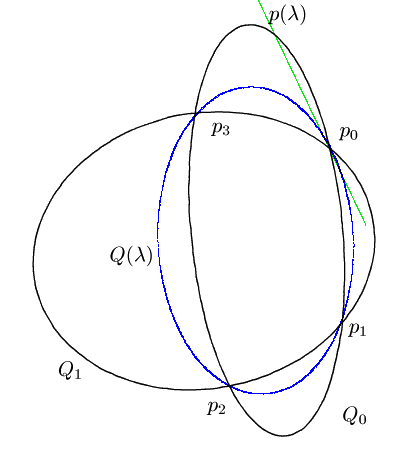
 と
と の4つの交点を
の4つの交点を
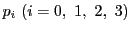 とし
とし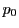 における
における の接線を
の接線を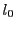 とする.
とする.
 の単位元として
の単位元として
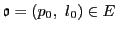 をとる.
そして
をとる.
そして
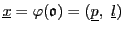 とおく.
とおく.
これを用いるとポンスレ条件は次のように表される.
命題 111
自然数

に対して,

の任意の元
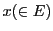
にはじまるポンスレ

角形存在するための
必要十分条件は,
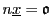
となることである.
■
この命題は次の事実から示される.
命題 112
対合の合成である

の自己同型

は,ある定点
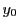
を用いて
と表される.
■
これは代数的にも解析的にも証明される.『代数幾何学』[38]等参照.
ところが
より
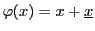 となる.この結果
となる.この結果
となる.よって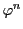 が恒等写像であることと
が恒等写像であることと
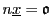 が同値となる.
が同値となる.
以上の考察は,ポンスレ条件を求めるために準備として行ったのであるが,
この時点でポンスレの定理110そのものは証明される.
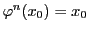 となる
となる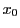 が存在すれば,
が存在すれば,
より
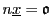 が結論され,
が結論され,
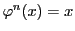 がすべての
がすべての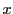 で成立する.
□
で成立する.
□
これが楕円曲線によるポンスレの定理の証明である.
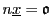 となるような
となるような
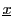 を
を 分点という.
分点という.
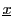 が
が 分点となる
分点となる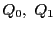 の条件,
それがポンスレ条件である.
それを具体的に記述するために,
の条件,
それがポンスレ条件である.
それを具体的に記述するために, にあわせて
さらにこれと同型な二つの楕円曲線,
線束楕円曲線と複素平面のトーラスで定まる楕円曲線を導入する.
にあわせて
さらにこれと同型な二つの楕円曲線,
線束楕円曲線と複素平面のトーラスで定まる楕円曲線を導入する.
ここで,線束楕円曲線とポンスレ対応曲線の同型を,
具体的な対応まで含めて,解析的方法で証明する.
定義108で定義された線束楕円曲線を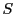 とする.
とする.
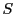 を非斉次座標で考えその方程式を
を非斉次座標で考えその方程式を
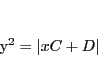 |
(5.21) |
とする.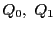 が一般の位置にあるので,系91.1より
3次方程式
が一般の位置にあるので,系91.1より
3次方程式
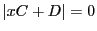 は相異なる3根
は相異なる3根
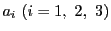 をもつ.
をもつ.
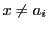 のときは
のときは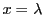 に対して
に対して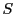 の2点
の2点
が対応する.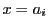 のときは1点
のときは1点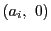 が対応し,
が対応し,
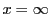 のときは1点
のときは1点
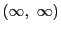 が対応する.
が対応する.
 次に
次に の点と複素数
の点と複素数 の対応を次のように定める.
の対応を次のように定める.
曲線束の曲線 に
に を通る接線を引き,
その接線と
を通る接線を引き,
その接線と の交点のうち
の交点のうち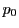 でないものを
でないものを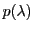 とする.
とする.
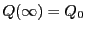 ,
,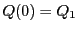 なので,
なので,
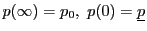 である.
また
である.
また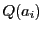 は退化二次曲線,つまり4交点を通る2直線であるから,
は退化二次曲線,つまり4交点を通る2直線であるから,
である.
したがって
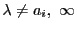 の
の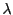 に対しては,
に対しては,
 の2点が対応し,
の2点が対応し,
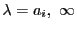 に対しては1点が対応する.
に対しては1点が対応する.
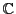 と
と の対応において,
の対応において,
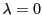 に対応する
に対応する の2点
の2点
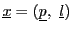 と
と
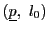 のうち
のうち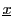 をとる.
をとる.
 と
と の対応において,
の対応において,
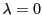 に対応する
に対応する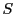 の2点
の2点
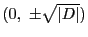 のいずれかをとる.
ここでは
のいずれかをとる.
ここでは
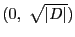 をとるものとする.
をとるものとする.
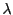 に対応する
に対応する と
と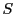 のそれぞれ2点のうち,
ここからの解析接続で定まる方をとる.
これによって
のそれぞれ2点のうち,
ここからの解析接続で定まる方をとる.
これによって と
と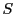 の間の一対一対応
の間の一対一対応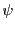 が定義される.
が定義される.
命題 113
対応
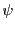
は,
定義
5.20で定まる楕円曲線
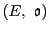
と,
方程式
5.21で定義された線束楕円曲線
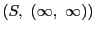
の
同型対応である.
■
注意 5.3.4
私は当初,ケーリーの第113論文と『代数幾何学』[
38]を学んだ段階で,
命題
109に続く証明のような形で同型を示した.
しかしこれは点の対応まで見通せていないものであり,
このままではポンスレ条件の導出はできなかった.
線束楕円曲線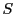 はまた,複素平面から作られるトーラスをリーマン面とする楕円曲線と同型である.
はまた,複素平面から作られるトーラスをリーマン面とする楕円曲線と同型である.
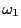 ,
,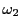 を比が実数倍でない二つの複素数とする.
を比が実数倍でない二つの複素数とする.
をこれらで張られる格子とする.
このとき商集合
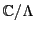 はトーラストなる.
はトーラストなる.
次にこの格子に対してワイエルシュトラスの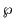 関数を次の無限級数で定義する.
関数を次の無限級数で定義する.
和は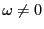 である
である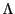 全体にわたる.定義から
全体にわたる.定義から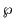 は
は
という二重周期関数である.
次の命題が成り立つ.
命題 114
- i)
- 級数
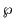 は
は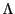 と交わらない任意のコンパクトな領域で一様に収束する.したがって
と交わらない任意のコンパクトな領域で一様に収束する.したがって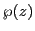 は
は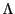 を除く
を除く のうえで解析的である.そして
のうえで解析的である.そして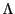 の各点で2位の極をもつ.
の各点で2位の極をもつ.
- ii)
- すべての
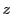 に対して
に対して
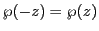 である.
である.
- iii)
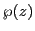 は
は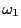 ,
,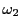 を周期とする楕円関数である.
■
を周期とする楕円関数である.
■
この基礎のうえに次の事実が成り立つ.
命題 115
- i)
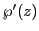 は
は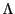 の各点で3位の極をもつ楕円関数である.
の各点で3位の極をもつ楕円関数である.
- ii)
-
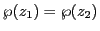 は,
は,
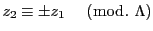 と同値である.
と同値である.
- iii)
 で定まる2定数
で定まる2定数 を
を
とおくと
が成り立つ.
- iv)
- 3次方程式
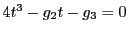 は相異なる3根をもち,
それは
は相異なる3根をもち,
それは
で与えられる.
■
また は次の形の加法定理をもつ.
これは加法定理(5.12)からの直接の帰結でもある.
は次の形の加法定理をもつ.
これは加法定理(5.12)からの直接の帰結でもある.
命題 116
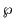
関数の加法公式:
が成り立つ.■
命題 117
3次方程式
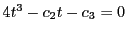
が重根をもたないとき,
つまりその判別式
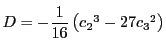
に関して
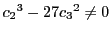
が成り立つとき,
格子
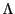
で
となるものが存在する.
■
3次方程式
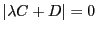 は相異なる3根
は相異なる3根
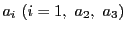 をもつ.行列
をもつ.行列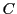 や
や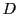 は定数倍の同値類の代表であるから,
は定数倍の同値類の代表であるから,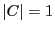 にとれる.このとき線束楕円曲線
にとれる.このとき線束楕円曲線 の方程式(5.21)は
の方程式(5.21)は
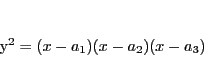 |
(5.22) |
と因数分解される.このとき を
を
 と表す.
と表す.
命題 118
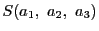
に対して格子
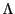
が存在し,
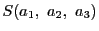
は楕円曲線
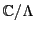
と同型になる.
逆に任意の格子
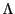
に対し
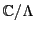
と
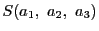
が同型となる
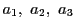
が存在する.
■
この対応は次のようになされる.
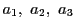 に対して
に対して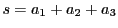 とし,
とし,
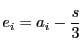 とおくと
とおくと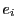 の和は0なので,
系117.1より格子
の和は0なので,
系117.1より格子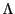 でその
でその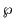 関数が
関数が
となるものが存在する.
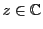 に対して
に対して
とおくと,この が
が
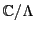 から
から
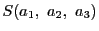 への同型を与える.
への同型を与える.
この二つの同型で の点
の点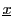 に対応する
に対応する
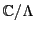 の点を
の点を
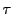 とする.
とする.
したがって,ポンスレ条件111は
この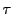 に関して
に関して
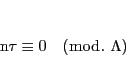 |
(5.23) |
が成り立つ条件と言いかえることが出来た.
ここで楕円関数に関する古典的な事実を用いる.
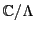 上の有理型関数を楕円関数と言った.
次の命題が成立する.
上の有理型関数を楕円関数と言った.
次の命題が成立する.
楕円関数で,0において高々 位の極をもつものの集合を
位の極をもつものの集合を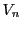 とする.
とする.
命題 120
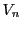
は
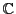
上の

次元ベクトル空間である.
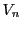
の基底として
をとることが出来る.
■
ポンスレ条件5.23は
命題119のiv)の条件において
としたものである.命題119のiv)から,
ポンスレ条件5.23は,
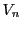 の楕円関数
の楕円関数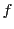 で,
で,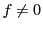 かつ
かつ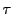 で
で 位の零点をもつものが存在すること,
と同値である.
このとき,
位の零点をもつものが存在すること,
と同値である.
このとき,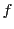 は必然的に0で
は必然的に0で 位の極をもつ.
位の極をもつ.
命題 121
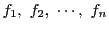
を
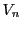
の基底とする.
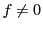
かつ
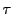
で

位の零点をもつものが存在する条件は,
とおくとき,
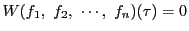
となることと同値である.
■
注意 5.3.5
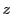
の関数
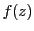
が
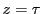
で解析的で
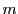
位の零点をもてば
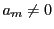
で
と展開される.
ここで
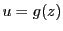
で
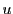
が
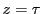
で解析的で
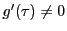
とする.
つまり
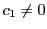
で
と展開されたとする.
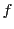
を
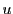
の関数と見たとき,
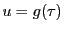
で

位の零点をもつとする.このとき
となるので,
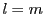
である.
したがって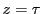 で位数
で位数 の零点をもつ関数の存在条件である,
条件
の零点をもつ関数の存在条件である,
条件
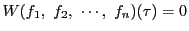 は,
は,
 を
を の関数と見たときの
条件
の関数と見たときの
条件
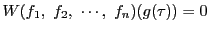 と同値である.
と同値である.
以上の準備のもとにポンスレ条件を と
と の行列
の行列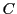 と
と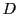 で書き表すケーリーの定理が証明される.
で書き表すケーリーの定理が証明される.
線束楕円曲線
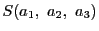 と.
トーラスで出来る楕円曲線
と.
トーラスで出来る楕円曲線
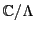 が同型となる格子
が同型となる格子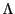 をとり,それによって定まる関数
をとり,それによって定まる関数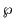 をとる.
をとる.
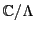 から
から
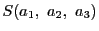 への同型を
への同型を
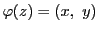 とすると
とすると
となり,この同型で
となるのであった.
定理 16
とする.このときポンスレ条件は,
- i)
-
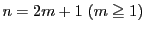 のとき
のとき
- ii)
-
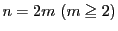 のとき
のとき
と同値である.
■
証明
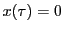 であり
であり
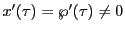 である.
したがって注意5.3.5によって,
条件
である.
したがって注意5.3.5によって,
条件
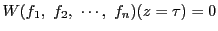 は
条件
は
条件
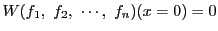 と同値である.
と同値である.
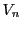 の基底として
の基底として
をとる.この基底を用いて
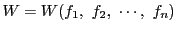 を計算する.
を計算する.
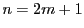 の場合に示す.
の場合に示す.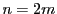 の場合も同様である.
非負整数
の場合も同様である.
非負整数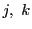 に対して
に対して
また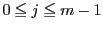 に対して
に対して
であるから
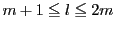 に対して
に対して
となる.これより は
は
と分けられる.ここで
 は
は
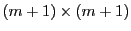 の対角行列式で,成分は
の対角行列式で,成分は
 である.
である.
 は
は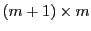 の行列式,
の行列式,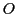 は
は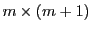 の零行列式である.そして
の零行列式である.そして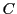 は
は
これより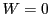 と
と
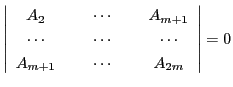 の同値性が示された.
□
の同値性が示された.
□
例 5.3.1
命題
99の記号を用いると
である.
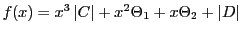
とおく.
これより得られる
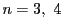
の結論が,
定理
14と命題
100に他ならない.
注意 5.3.6
すでに,
線型代数を用いる証明の中で
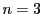
,
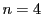
の場合を示した.
そこでは
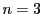
のときは必要十分条件であることまで示せたが,
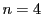
の場合は注意
5.1.2に書いたように,
十分性しか示せていなかった.
ところが上記定理によって,

と

が一般の位置にあるという条件の下で,
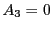
が必要十分条件であることが示された.
当初考えた課題のうち,次の二つがまだ出来ていない.
一つは,ケーリー条件の代数的証明をめざす,ことである.
もう一つは,退化した場合のポンスレの定理を,統一して扱うことである.
後者については,『Poncelet's Theorem』[40]でなされている.
時間が許せば,ここで再構成したいと考えている.
ポンスレの定理は,さらに空間の二次曲面や,多くの展開がある.
『Poncelet Porisms and Beyond』[41]には,現在の到達点まで述べられている.
前者については,代数幾何のさらに深い構成が必要で,
現在の力に余る.
このような課題を確認して,とりあえず一区切りとしたい.


 次: むすび
上: 代数幾何へ
前: 楕円関数による証明
2014-01-03
次: むすび
上: 代数幾何へ
前: 楕円関数による証明
2014-01-03
![]() と
と![]() の方程式を
の方程式を
![]() ,
,
![]() として一般性を失わない.
として一般性を失わない.
![]() は
は
![]() と
と![]() が一般の位置にあれば,
が一般の位置にあれば,
![]() ,
,![]() ,
,![]() は相異なり,
ワイエルシュトラスの
は相異なり,
ワイエルシュトラスの![]() 関数
といわれる非特異な楕円曲線である.
□
関数
といわれる非特異な楕円曲線である.
□
![]() の点は
の点は![]() の直線に対応する.
の直線に対応する.![]() の点と
の点と![]() の直線を同一視する.
2つの円錐曲線の直積集合
の直線を同一視する.
2つの円錐曲線の直積集合
![]() の部分集合
の部分集合![]() を次のように定める.
を次のように定める.
![]() と
と![]() の方程式を
の方程式を
![]() ,
,
![]() として一般性を失わない.
このとき楕円曲線
として一般性を失わない.
このとき楕円曲線![]() は方程式
は方程式
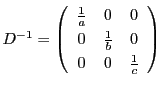 であるから
であるから![]() は方程式
は方程式
![]() より
より
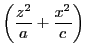 をかけて平方完成して
をかけて平方完成して
 とする.
とする.
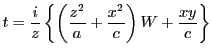 とおく.
とおく.
![]() は
は
![]() という媒介変数表示をもつので,
という媒介変数表示をもつので,
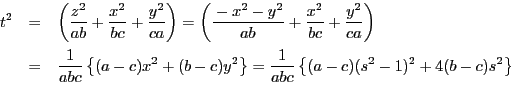
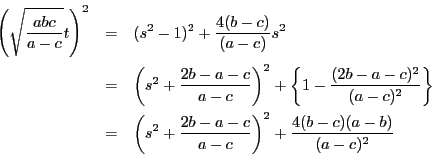
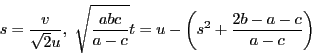
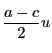 を
を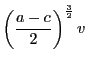 を
を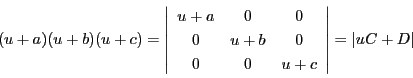
![]() に解析構造を入れ,リーマン面としこれが楕円曲線であることを示す,
という方向でもなされる.これは後におこなう.
に解析構造を入れ,リーマン面としこれが楕円曲線であることを示す,
という方向でもなされる.これは後におこなう.
![]() と
と![]() との他の交点を
との他の交点を![]() とする.これによって
写像
とする.これによって
写像
![]() とその上の対合の合成に関する命題としてとらえることができる.
この命題そのものは,われわれもさまざまの方法で証明してきた.
さらに次に示すような代数群としての
とその上の対合の合成に関する命題としてとらえることができる.
この命題そのものは,われわれもさまざまの方法で証明してきた.
さらに次に示すような代数群としての![]() の演算を用いる証明が出来る.
の演算を用いる証明が出来る.
 ここでケーリーからグリヒスに引き継がれた考え方を用いる.
ここでケーリーからグリヒスに引き継がれた考え方を用いる.![]() と
と![]() の4つの交点を
の4つの交点を
![]() とし
とし![]() における
における![]() の接線を
の接線を![]() とする.
とする.
![]() の単位元として
の単位元として
![]() をとる.
そして
をとる.
そして
![]() とおく.
とおく.![]() とする.
とする.
![]() を非斉次座標で考えその方程式を
を非斉次座標で考えその方程式を
 次に
次に![]() の点と複素数
の点と複素数![]() の対応を次のように定める.
の対応を次のように定める.
![]() に
に![]() を通る接線を引き,
その接線と
を通る接線を引き,
その接線と![]() の交点のうち
の交点のうち![]() でないものを
でないものを![]() とする.
とする.
![]() ,
,![]() なので,
なので,
![]() である.
また
である.
また![]() は退化二次曲線,つまり4交点を通る2直線であるから,
は退化二次曲線,つまり4交点を通る2直線であるから,
![]() の
の![]() に対しては,
に対しては,
![]() の2点が対応し,
の2点が対応し,
![]() に対しては1点が対応する.
に対しては1点が対応する.![]() と
と![]() の対応において,
の対応において,
![]() に対応する
に対応する![]() の2点
の2点
![]() と
と
![]() のうち
のうち![]() をとる.
をとる.
![]() と
と![]() の対応において,
の対応において,
![]() に対応する
に対応する![]() の2点
の2点
![]() のいずれかをとる.
ここでは
のいずれかをとる.
ここでは
![]() をとるものとする.
をとるものとする.
![]() に対応する
に対応する![]() と
と![]() のそれぞれ2点のうち,
ここからの解析接続で定まる方をとる.
これによって
のそれぞれ2点のうち,
ここからの解析接続で定まる方をとる.
これによって![]() と
と![]() の間の一対一対応
の間の一対一対応![]() が定義される.
が定義される.
![]() ,
,![]() を比が実数倍でない二つの複素数とする.
を比が実数倍でない二つの複素数とする.
![]() 関数を次の無限級数で定義する.
関数を次の無限級数で定義する.
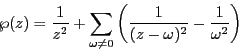
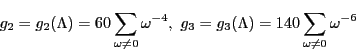
![]() は次の形の加法定理をもつ.
これは加法定理(5.12)からの直接の帰結でもある.
は次の形の加法定理をもつ.
これは加法定理(5.12)からの直接の帰結でもある.
![]() に対して
に対して![]() とし,
とし,
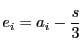 とおくと
とおくと![]() の和は0なので,
系117.1より格子
の和は0なので,
系117.1より格子![]() でその
でその![]() 関数が
関数が
![]() の点
の点![]() に対応する
に対応する
![]() の点を
の点を
![]() とする.
とする.
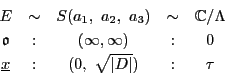
![]() に関して
に関して
![]() 位の極をもつものの集合を
位の極をもつものの集合を![]() とする.
とする.
![]() で位数
で位数![]() の零点をもつ関数の存在条件である,
条件
の零点をもつ関数の存在条件である,
条件
![]() は,
は,
![]() を
を![]() の関数と見たときの
条件
の関数と見たときの
条件
![]() と同値である.
と同値である.
![]() と.
トーラスで出来る楕円曲線
と.
トーラスで出来る楕円曲線
![]() が同型となる格子
が同型となる格子![]() をとり,それによって定まる関数
をとり,それによって定まる関数![]() をとる.
をとる.
![]() から
から
![]() への同型を
への同型を
![]() とすると
とすると
![]() の基底として
の基底として
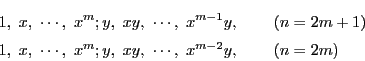
![]() の場合に示す.
の場合に示す.![]() の場合も同様である.
非負整数
の場合も同様である.
非負整数![]() に対して
に対して
![\begin{displaymath}
\dfrac{d}{dx^j}x^k\biggr]_{x=0}=
\left\{
\begin{array}{cc}
0,&(j\ne k)\\
j!&(j=k)
\end{array}
\right.
\end{displaymath}](images/img3264.gif)
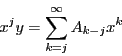
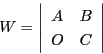

![]() と
と
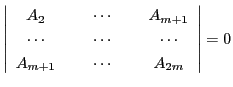 の同値性が示された.
□
の同値性が示された.
□