

 次: 存在条件の導出
上: 代数幾何へ
前: 射影幾何と代数幾何
次: 存在条件の導出
上: 代数幾何へ
前: 射影幾何と代数幾何
ケーリー(Arthur Cayley)の論文集第2巻[42]所収の第113論文の方法を再構成する.本節ではケーリーの方法によってポンスレの定理12の楕円関数による証明をおこなう.
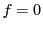 と
と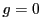 を二つの円錐曲線
を二つの円錐曲線 と
と の方程式とする.
命題90に示したように,同じ曲線束に属する円錐曲線
の方程式とする.
命題90に示したように,同じ曲線束に属する円錐曲線 の方程式は,
の方程式は,
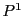 の点
の点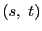 を用いて
を用いて
と表される.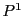 の点
の点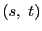 を用いる代わりに,
を用いる代わりに,
 を含めて
を含めて
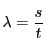 とおき,
方程式を
とおき,
方程式を
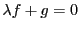 としてもよい.
このようにして定まる曲線束の曲線を
としてもよい.
このようにして定まる曲線束の曲線を
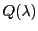 と表すのであった.
と表すのであった.
 の直線
の直線 に対して
に対して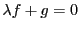 がこれと接するとする.
がこれと接するとする.
 の方程式を用いて
の方程式を用いて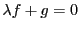 の一文字を消去すれば,
他の残る二文字の2次同次方程式が得られる.この判別式を0とおくことによって,
の一文字を消去すれば,
他の残る二文字の2次同次方程式が得られる.この判別式を0とおくことによって,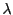 の2次方程式が得られる.つまり
の2次方程式が得られる.つまり に接する曲線束の曲線を定める
に接する曲線束の曲線を定める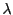 の値は一般に2個ある.
の値は一般に2個ある.
以下では と
と を次のように定める.
命題95によって,
一般の位置にある2つの円錐曲線は
射影変換によって次の形にすることができる.
を次のように定める.
命題95によって,
一般の位置にある2つの円錐曲線は
射影変換によって次の形にすることができる.
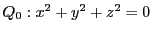 とする.
とする.
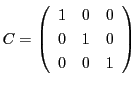 である.
である.
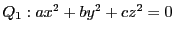 とする.
とする.
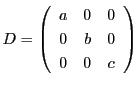 である.
である.
二つの方程式を連立して解くと
となり,
 と
と が相異なる4点で交わるという条件は,
が相異なる4点で交わるという条件は,
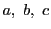 がすべて異なるという条件と同値である.
がすべて異なるという条件と同値である.
補題 23
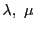
は異なるとする.
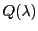
と
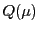
の共通接線は4本あり,
接線の方程式は
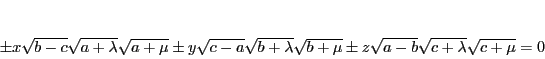 |
(5.7) |
である.
■
証明
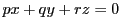 が
が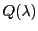 と
と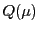 に接するとする.
に接するとする.
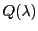 と
と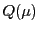 の方程式は
の方程式は
である.
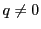 であるとし,第1式で
であるとし,第1式で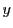 を消去する.
を消去する.
これが2次同次方程式として重根もつ.その判別式をとって
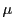 についても同様に成り立ち,
についても同様に成り立ち,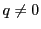 としたので
としたので
である.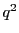 を消去して
を消去して
同様にして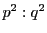 も定まり,次式を得る.
も定まり,次式を得る.
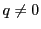 としたが,得られた結果の対称性から,他の場合も同様である.
これから共通接線の方程式(5.7)を得る.
□
としたが,得られた結果の対称性から,他の場合も同様である.
これから共通接線の方程式(5.7)を得る.
□
命題 103
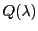
と
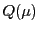
の共通接線が

と2点
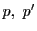
で交わるとする.

における

の接線が
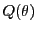
に接するとする.
このとき等式
が成立するように根号の符号を選ぶことができる.
逆にこの関係式が成立するように平方根の符号をとることができれば,
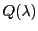 と
と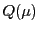 の共通接線と
の共通接線と の交点を
の交点を とするとき,
とするとき,
 での
での の接線は
の接線は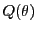 に接する.
■
に接する.
■
証明
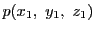 とおく.
とおく. における
における の接線は
の接線は
である.これが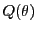 ,つまり
,つまり
に接する.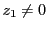 とする.これから
とする.これから
判別式をとって整理すると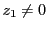 なので
なので
対称性から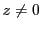 でないときも同様である.
でないときも同様である.
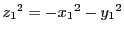 より
より
これらより
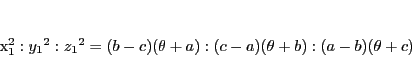 |
(5.9) |
が成り立つ.
符号を適切にとり,その ときの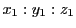 が
方程式(5.7)の
が
方程式(5.7)の
の上にあるようにする.
このとき等式(5.8)が成立する.
逆にこのとき,
は(5.9)を満たす 上の点であり,ここでの接線が
上の点であり,ここでの接線が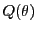 に接している.
□
に接している.
□
注意 5.3.1
等式(
5.8)は
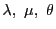
に関して対称である.
したがって,
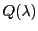
と
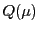
の共通接線と

の交点における

の接線が
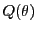
に接するならば,
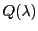
と
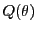
の共通接線と

の交点における

の接線は
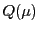
に接し,
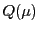
と
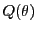
の共通接線と

の交点における

の接線も
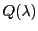
に接する.
これを例示するために,さらに
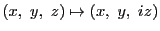
の座標変換をおこない,
実平面に描いてみる.
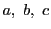 を相異なる定数として
を相異なる定数として
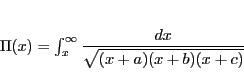 |
(5.10) |
とおく.
補題 24
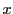
と
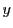
に対して
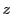
を
で定める.このとき
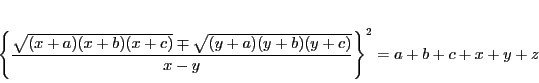 |
(5.11) |
が成り立つ.
■
証明
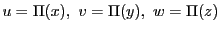 とし,
とし,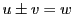 とおいて
とおいて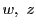 を固定する.
を固定する.
である.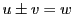 が固定されているので
が固定されているので
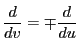 .よって
.よって
である.
一方,
であるから
両辺に
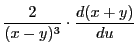 を乗じて
を乗じて
両辺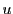 で積分して
で積分して
を得る.積分定数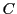 は
は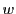 で決まる.
これを明示してこの等式は
で決まる.
これを明示してこの等式は
となる.次にこの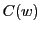 を決定する.
を決定する.
ここで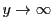 をとると
をとると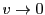 となり
となり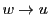 である.
よって
である.
よって
この結果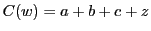 となり,等式(5.11)が成立する.
□
となり,等式(5.11)が成立する.
□
一般に
とおくと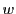 は
は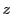 の関数であるが,
その逆関数をヤコビの楕円関数と言い
の関数であるが,
その逆関数をヤコビの楕円関数と言い
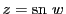 と表す.
と表す.
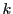 を母数,
を母数,
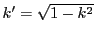 を補母数という.
そして
を補母数という.
そして
とおくと,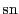 関数は
関数は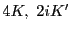 を基本周期とする二重周期関数で,
奇関数である.
を基本周期とする二重周期関数で,
奇関数である.
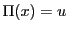 に対してその逆関数を
に対してその逆関数を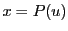 とおく.
とおく.
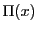 の定義(5.10)
において
の定義(5.10)
において
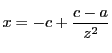 とおきかえる.
とおきかえる.
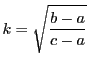 とすると,
とすると,
となる.
したがって,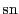 を用いると
を用いると
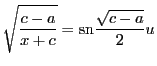 が成り立つ.
これを
が成り立つ.
これを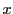 について解いて
について解いて
を得る.これが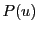 の楕円関数
の楕円関数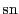 による表示である.
これからまた
による表示である.
これからまた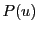 は偶関数である.
は偶関数である.
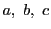 が実数の場合,
が実数の場合,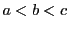 とすると
積分(5.10)はまず
とすると
積分(5.10)はまず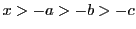 で定義され,
その逆関数を複素平面全体に解析接続したものが
で定義され,
その逆関数を複素平面全体に解析接続したものが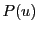 である.
実数でない場合も同様に考えることができる.
である.
実数でない場合も同様に考えることができる.
等式(5.11)は楕円関数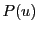 の加法定理である.
実際,
の加法定理である.
実際,
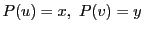 とすると,
関係式
とすると,
関係式
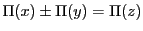 は
は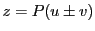 を意味する.
そして
を意味する.
そして
であるから,等式(5.11)は
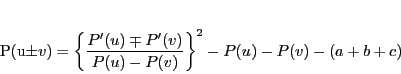 |
(5.12) |
となる.
注意 5.3.2
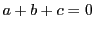
の場合の
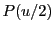
がいわゆるワイエルシュトラスの
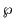
関数である.
命題 104
等式
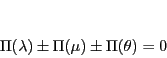 |
(5.13) |
が成り立つ符号のとり方が存在することは等式(
5.8)
が成立することと同値である.
■
証明
等式(5.13)は
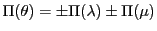 であるから,
補題24によって,この等式は補題24の
であるから,
補題24によって,この等式は補題24の
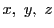 を
を
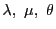 をに変えた等式
をに変えた等式
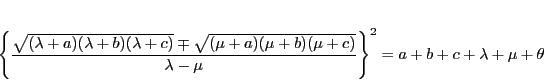 |
(5.14) |
を意味する.
よって等式(5.8)と,
符号を適当にとることで等式(5.14)の成立する
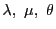 が存在することとが同値であること,
これが証明すべきことである.
いいかえると,根号部分の平方計算を経て2式が同一の式なることが証明すべきことである.
が存在することとが同値であること,
これが証明すべきことである.
いいかえると,根号部分の平方計算を経て2式が同一の式なることが証明すべきことである.
次に,同様にして
となる.
それぞれが同一の式に同値変形されたので,
等式(5.14)となるように符号がとれることは
等式(5.8)となるように符号がとれることと同値であることが示された.
□
系 104.1
等式(5.13)が成り立つ符号のとり方が存在することは,
等式
が成立する符号のとり方が存在することと同値である.
証明
等式(5.13)は等式(5.15)と同値になった.
ところがこの式は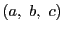 と
と
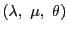 に関して対称である.
よってこれを入れ替え,上記命題の等式(5.8)から等式(5.16)
にいたる同値変形を逆にたどることで等式(5.17)を得る.
□
に関して対称である.
よってこれを入れ替え,上記命題の等式(5.8)から等式(5.16)
にいたる同値変形を逆にたどることで等式(5.17)を得る.
□
注意 5.3.3
等式(
5.17)は行列式では
と表される.
ケーリーの定理は,
曲線束の2つの円錐曲線
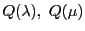 に接する接線の
に接する接線の との交点における接線が
との交点における接線が
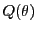 と接しているとき,
と接しているとき,
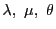 を楕円積分の関係式に表すことができるということであった.
この定理をもとに,ポンスレの定理12の別証明をおこなう.
を楕円積分の関係式に表すことができるということであった.
この定理をもとに,ポンスレの定理12の別証明をおこなう.
命題 105
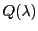
と
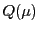
の共通接線が

と異なる2点
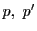
で交わるとする.
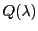
の接線が

と交わる点を
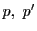
とする.

と
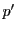
での

の接線が
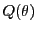
,
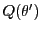
と接しているとする.
このとき,
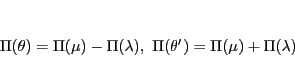 |
(5.18) |
となるように符号をとることができる.
■
証明
命題104によって
となるように符号がとれる.ここで2式の右辺の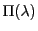 と
と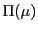 の符号が
いずれも同符号,またはいずれも異符号であれば,
の符号が
いずれも同符号,またはいずれも異符号であれば,
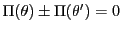 となる.
となる.
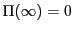 なのでこれは
なのでこれは
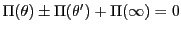 を意味する.
このとき
を意味する.
このとき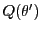 と
と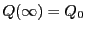 の共通接線と
の共通接線と の交点は
の交点は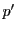 のみであり,
その点での
のみであり,
その点での の接線が
の接線が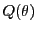 と接すること意味し,
と接すること意味し,
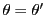 である.
である. と
と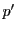 が異なることに反する.
が異なることに反する.
よって一方が同符号で一方が異符号なので,適当に符号をとることによって
(5.18)の形にすることができる.
□
このとき,関係式
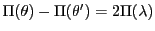 が成り立つが,
逆も成立する.
が成り立つが,
逆も成立する.
命題 106
変数
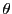
と
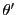
が関係式
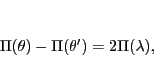 |
(5.19) |
となるように符号をとることができるなら,

と
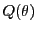
の共通接線の

の接点を

,

と
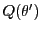
の共通接線の

の接点を
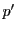
とするとき,
直線
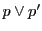
は
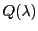
に接する.
■
証明
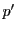 を通る
を通る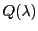 の接線を
の接線を とする.曲線束の曲線で
とする.曲線束の曲線で と接するものを
と接するものを
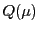 とする.このとき
とする.このとき
となるように符号を選ぶことができ,条件から
も成立し, は
は を通る.つまり直線
を通る.つまり直線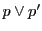 は
は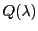 に接する.
□
に接する.
□
以上の準備によって,
ポンスレの定理12の楕円積分による証明ができる.
ポンスレの定理12を,曲線束の記号を用いて再掲する.
自然数 を
を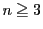 とする.
与えられた円錐曲線
とする.
与えられた円錐曲線 上に頂点をもつ
上に頂点をもつ 角形
角形
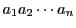 がある.
辺
がある.
辺
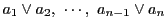 はそれぞれ
はそれぞれ と同じ曲線束に属する
円錐曲線
と同じ曲線束に属する
円錐曲線
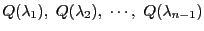 に接している.
このとき残る辺
に接している.
このとき残る辺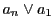 も同じ曲線束に属するある円錐曲線
も同じ曲線束に属するある円錐曲線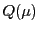 に接する.
■
に接する.
■
証明
が成り立っている.
ここで
となるように符号のとれる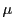 をとる.
このとき
をとる.
このとき
も成り立ち,
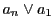 は同じ曲線束に属する円錐曲線
は同じ曲線束に属する円錐曲線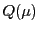 に接する.
□
に接する.
□
同様に閉形定理13が示される.
定理を再掲する.
自然数 を
を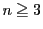 とする.
与えられた円錐曲線
とする.
与えられた円錐曲線 上に頂点をもつ
上に頂点をもつ 角形
角形
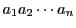 で,
辺
で,
辺
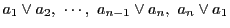 が
それぞれ
が
それぞれ と同じ曲線束に属する
円錐曲線
と同じ曲線束に属する
円錐曲線
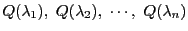 に接しているものが存在する.
このとき,
に接しているものが存在する.
このとき, 上の任意の点
上の任意の点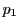 をとり,順次
をとり,順次
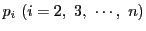 を
を
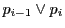 が
が
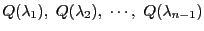 に接するようにとる.このとき残る辺
に接するようにとる.このとき残る辺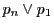 も
も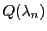 に接する.
■
に接する.
■
証明
一つの 角形の存在によって
角形の存在によって
となる.その結果,
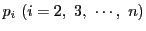 を
を
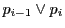 が
が
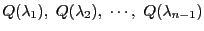 に接するなら,上記記号で
に接するなら,上記記号で
も成り立ち,このとき残る辺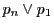 も
も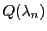 に接する.
□
に接する.
□


 次: 存在条件の導出
上: 代数幾何へ
前: 射影幾何と代数幾何
2014-01-03
次: 存在条件の導出
上: 代数幾何へ
前: 射影幾何と代数幾何
2014-01-03
![]() の直線
の直線![]() に対して
に対して![]() がこれと接するとする.
がこれと接するとする.
![]() の方程式を用いて
の方程式を用いて![]() の一文字を消去すれば,
他の残る二文字の2次同次方程式が得られる.この判別式を0とおくことによって,
の一文字を消去すれば,
他の残る二文字の2次同次方程式が得られる.この判別式を0とおくことによって,![]() の2次方程式が得られる.つまり
の2次方程式が得られる.つまり![]() に接する曲線束の曲線を定める
に接する曲線束の曲線を定める![]() の値は一般に2個ある.
の値は一般に2個ある.
![]() と
と![]() を次のように定める.
命題95によって,
一般の位置にある2つの円錐曲線は
射影変換によって次の形にすることができる.
を次のように定める.
命題95によって,
一般の位置にある2つの円錐曲線は
射影変換によって次の形にすることができる.
![]() とする.
とする.
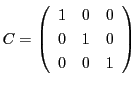 である.
である.
![]() とする.
とする.
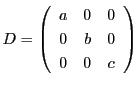 である.
である.
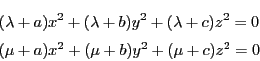
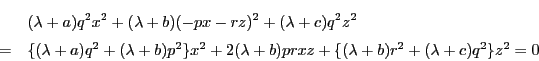
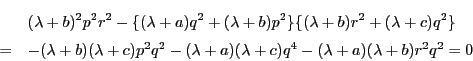
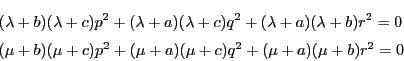
![]() としたが,得られた結果の対称性から,他の場合も同様である.
これから共通接線の方程式(5.7)を得る.
□
としたが,得られた結果の対称性から,他の場合も同様である.
これから共通接線の方程式(5.7)を得る.
□
![]() と
と![]() の共通接線と
の共通接線と![]() の交点を
の交点を![]() とするとき,
とするとき,
![]() での
での![]() の接線は
の接線は![]() に接する.
■
に接する.
■
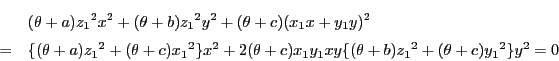
![]() が
方程式(5.7)の
が
方程式(5.7)の

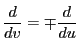 .よって
.よって
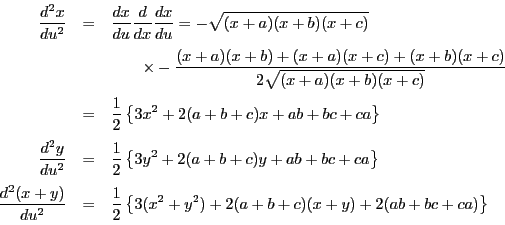
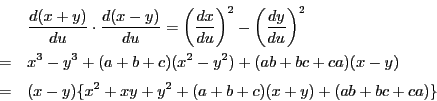
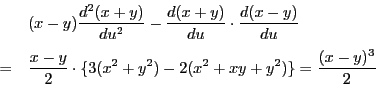
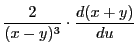 を乗じて
を乗じて
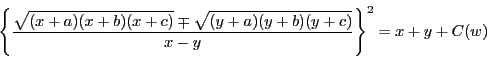
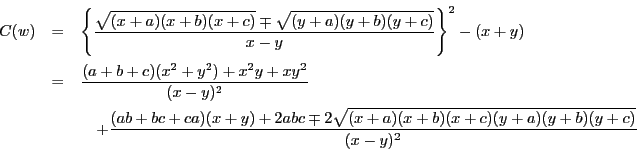
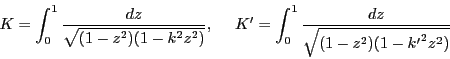
![]() の定義(5.10)
において
の定義(5.10)
において
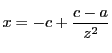 とおきかえる.
とおきかえる.
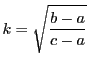 とすると,
とすると,
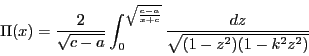
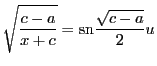 が成り立つ.
これを
が成り立つ.
これを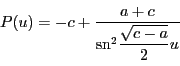
![]() が実数の場合,
が実数の場合,![]() とすると
積分(5.10)はまず
とすると
積分(5.10)はまず![]() で定義され,
その逆関数を複素平面全体に解析接続したものが
で定義され,
その逆関数を複素平面全体に解析接続したものが![]() である.
実数でない場合も同様に考えることができる.
である.
実数でない場合も同様に考えることができる.
![]() の加法定理である.
実際,
の加法定理である.
実際,
![]() とすると,
関係式
とすると,
関係式
![]() は
は![]() を意味する.
そして
を意味する.
そして
![]() が成り立つが,
逆も成立する.
が成り立つが,
逆も成立する.
を
とする. 与えられた円錐曲線
上に頂点をもつ
角形
がある. 辺
はそれぞれ
と同じ曲線束に属する 円錐曲線
に接している. このとき残る辺
も同じ曲線束に属するある円錐曲線
に接する. ■
を
とする. 与えられた円錐曲線
上に頂点をもつ
角形
で, 辺
が それぞれ
と同じ曲線束に属する 円錐曲線
に接しているものが存在する. このとき,
上の任意の点
をとり,順次
を
が
に接するようにとる.このとき残る辺
も
に接する. ■