解1
![]() なので
なので ![]() が3の倍数なら明らかに9の倍数である.
が3の倍数なら明らかに9の倍数である.
3の倍数でないときに示す.![]() とおく.
とおく.
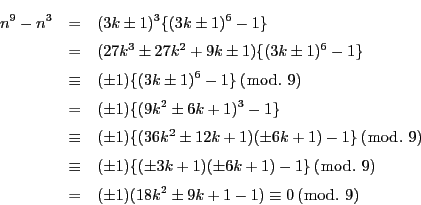
ゆえに
解2
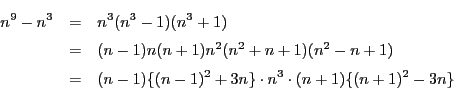
解1
![]() なので
なので ![]() が3の倍数なら明らかに9の倍数である.
が3の倍数なら明らかに9の倍数である.
3の倍数でないときに示す.![]() とおく.
とおく.
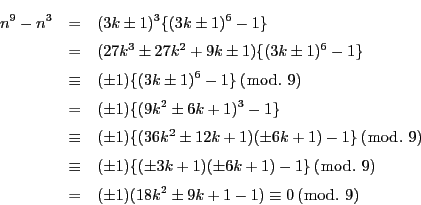
解2
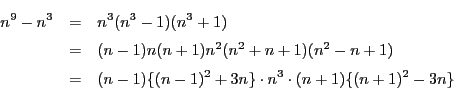
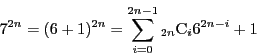
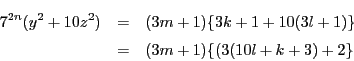
一方![]() を3で割ると0か1余る.ゆえに条件式の両辺を3で割った余りが
右辺と左辺で異なり矛盾である.
を3で割ると0か1余る.ゆえに条件式の両辺を3で割った余りが
右辺と左辺で異なり矛盾である.
したがって少なくとも![]() または
または![]() が3の倍数で,
が3の倍数で,![]() が3の倍数であることが示された.
が3の倍数であることが示された.
![]() のとき.条件式は
のとき.条件式は
![]() なので,
なので,![]() と
と![]() の偶数・奇数は一致する.ゆえに可能性があるのは
の偶数・奇数は一致する.ゆえに可能性があるのは
![]() のとき.
のとき.![]() が平方数.同様に
が平方数.同様に![]() とおく.
とおく.
したがって![]() .
.
![]() を
を![]() で割った商を
で割った商を![]() ,余りを
,余りを![]() とする.ここで自然数
とする.ここで自然数![]() に対して
に対して
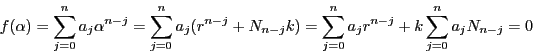
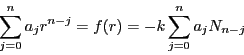
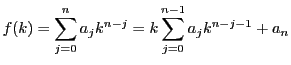 より,
より,
対偶が示され(2)が証明された.