史織 最初の教科書による必要条件・十分条件もはっきりしました.
二つの条件に対して,その含意命題
が真のとき
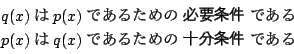
という.ということです.
南海 真理集合との関係で必要条件,十分条件を特徴づければどうなるのか.
史織
![]() が真ということは,
が真ということは,
![]() を真とする
を真とする ![]() はすべて
はすべて ![]() を真とする,ということですから,
これまでと同じく条件
を真とする,ということですから,
これまでと同じく条件 ![]() の真理集合を
の真理集合を ![]() と表すと
と表すと
ですから
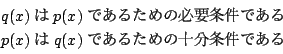
そして
![]() と
と
![]() がともに真のとき,
つまり
がともに真のとき,
つまり![]() は
は ![]() であるための 必要十分条件 であるとき,
2つの条件
であるための 必要十分条件 であるとき,
2つの条件![]() と
と ![]() は同値であるといいます.
は同値であるといいます.
南海
その通り.一点注意.同値性は定義域![]() をどのようにとるかで変わるということだ.
をどのようにとるかで変わるということだ.
![]() を実数にとれば,条件
を実数にとれば,条件 ![]() と
と
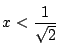 は同値ではない.しかし
は同値ではない.しかし
![]() を整数にとれば,条件
を整数にとれば,条件 ![]() と
と
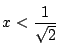 は同値である.
は同値である.
同値であることは,それぞれの真理集合が一致することだ.
![]() から
から![]() には下の選択肢(a),(b),(c),(d)から正しいものを選んで入れよ.
には下の選択肢(a),(b),(c),(d)から正しいものを選んで入れよ.