史織 これも教科書に載っています.
条件 ![]() に対して「
に対して「
![]() が真」は
が真」は
![]() を意味します.
一方「
を意味します.
一方「
![]() が真」は
が真」は
![]() を意味します.ところが一般に集合
を意味します.ところが一般に集合 ![]() に対して
に対して
![]() です.ここで
です.ここで
![]() は全体集合から集合
は全体集合から集合 ![]() の要素を取り除いたものです.
の要素を取り除いたものです.
したがって
南海
なかなかよく勉強している.
![]() や
や ![]() が自体が命題のときは
が自体が命題のときは![]() や
や ![]() を命題関数にして,同様に示せばよい.
を命題関数にして,同様に示せばよい.
南海 さて証明における推論の方法なのだが,ここで直接証明と間接証明について触れておこう.
典型的な直接証明 は次のように行われる.
それに対して間接証明とは何か.命題![]() を証明したいときに,自明であったりその証明の前提となっている
適当な命題
を証明したいときに,自明であったりその証明の前提となっている
適当な命題![]() を用いて
を用いて
![]() を示す.これから
を示す.これから
![]() が成り立つことが示され,
が成り立つことが示され,![]() を前提として
を前提として![]() が成立することを示すことができる.
が成立することを示すことができる.
これが背理法だ.これについては『高校数学の方法』「背理法」で 具体的に詳しく述べたので見てほしい.
最後にもう一題演習問題を.
次の二つの命題 ![]() ,
,![]() を考える.ただし
を考える.ただし ![]() は実数とする.
は実数とする.
![]() 未知数を
未知数を ![]() とする連立方程式
とする連立方程式
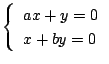 において,
において, ![]() 以外の解で,
以外の解で, ![]() かつ
かつ ![]() を満たすものがある.
を満たすものがある.
![]() ベクトル
ベクトル
![]() ,
,
![]() について
について
![]() かつ
かつ
![]() となるベクトル
となるベクトル
![]() がある.
がある.