交わらない二円
- 1)
- 最初の円
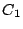 をどこにとっても順に外接させて円を描いてゆくと
をどこにとっても順に外接させて円を描いてゆくと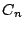 は
は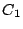 に外接する.
に外接する.
- 2)
- 二円
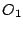 と
と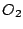 の中心間の距離を
の中心間の距離を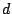 とする.
とする.
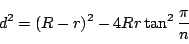
が成り立つ. ■

同心円の間に![]() 個の円が互いに外接してはさまれるときは,
半径だけが問題で,
個の円が互いに外接してはさまれるときは,
半径だけが問題で,![]() 個の円環が一つできればどこからはじめても
個の円環が一つできればどこからはじめても![]() 個で円環ができる.
最初
個で円環ができる.
最初![]() と
と![]() の間に
の間に![]() をかく.
その反転
をかく.
その反転![]() からはじめて同心円の方で
からはじめて同心円の方で![]() 個の円環をつくる.
これを反転の逆をおこないもとに戻せば
個の円環をつくる.
これを反転の逆をおこないもとに戻せば![]() からはじまる円環ができている.
からはじまる円環ができている.
2) ![]() と
と![]() を反転した円の半径を
を反転した円の半径を![]() とする.
この場合
とする.
この場合![]() 等の半径は
等の半径は
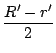 で,
で,
![]() と
と![]() の中心
の中心
![]() と
と
![]() が
が
![]() の中心
の中心
![]() となす角が
となす角が
![]() .
.
![]() の中心
の中心
![]() ,
,![]() と
と![]() の接点
の接点![]() ,
,
![]() の中心
の中心
![]() が作る直角三角形の辺長を考えることにより
が作る直角三角形の辺長を考えることにより

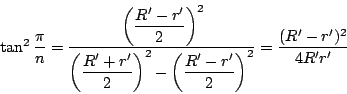
太郎
これを用いて冒頭の和算の問題を解いてみます.
丁円の半径を![]() ,丙円の半径を
,丙円の半径を![]() とする.
まず対称性から甲,丁,丙各円の中心は一直線上にある.
とする.
まず対称性から甲,丁,丙各円の中心は一直線上にある.
南海 文献『日本の幾何』には多くの問題が載っている. シュタイナーの円環に関するその他の定理を紹介しよう.
 証明
まず状況を確定する.
円
証明
まず状況を確定する.
円
点![]() を中心とする半径
を中心とする半径![]() の反転で
円
の反転で
円![]() ,
,![]() が同心円
が同心円![]() ,
,![]() になりその半径が
になりその半径が![]() とする.
とする.
![]() の半径はすべて等しいのでこれを
の半径はすべて等しいのでこれを![]() とする.
とする.
定理2の5)より
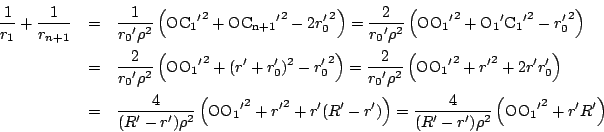
一方,定理2の5)を
![]() に用いて
に用いて
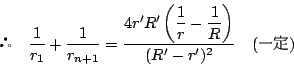
南海
定理6より![]() の中心間の距離を
の中心間の距離を![]() とすれば
とすれば
これは1826年に池田貞一が示した定理である(文献『幾何学』による).
特に![]() のときは
のときは