南海
それはいいところに気がついた.
反転は平面だけではなく,一般の![]() 次元ユークリッド空間で定義される.
そしてそれを用いて一般の空間で互いに接する球の諸性質を示すことができる.
次元ユークリッド空間で定義される.
そしてそれを用いて一般の空間で互いに接する球の諸性質を示すことができる.
ここでは三次元空間における反転をまとめ,その図形問題への応用を考えよう. そのために,平面の反転と根軸の部分を三次元に直してゆかなければならない.
太郎
空間の点![]() を中心とする半径
を中心とする半径
![]() の球がある.
の球がある.
![]() から半直線上に二点
から半直線上に二点
![]() をとる.
をとる.

証明
![]() の方程式を
の方程式を
反転の中心を原点におき,反転の定円の半径を![]() とする.
点
とする.
点
![]() と
点
と
点
![]() がこの円に関して反転であるとする.
すると
がこの円に関して反転であるとする.
すると
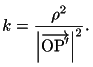 .
これから
.
これから
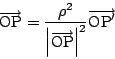
 も成り立つ.
点
も成り立つ.
点
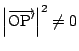 なので
なので

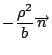 にあるので,
にあるので,
南海 平面の場合の根軸に対応することも, 空間の場合に確認しておかなければならない.
太郎
二球![]() の方程式を
の方程式を
![]() とする.
ただし,
とする.
ただし,![]() の係数は1にとっておく.このとき,
方程式
の係数は1にとっておく.このとき,
方程式
南海
この一次式で定まる平面を二球![]() の根面という.
図形的な意味は,根面上の点
の根面という.
図形的な意味は,根面上の点![]() から
から
![]() に接線が引けるとき,接点を
接点
に接線が引けるとき,接点を
接点
![]() とすれば
とすれば
太郎
また,二球![]() と
と![]() の根面上に中心をもつ球
の根面上に中心をもつ球![]() をとる.
球
をとる.
球![]() の
中心が
の
中心が
![]() ,
半径が
,
半径が![]() であるとする.
であるとする.
![]() とすると,
とすると,
![]() は
は
南海
二球![]() が共有点をもたないとする.
この二球の根面と二球
が共有点をもたないとする.
この二球の根面と二球![]() の中心を結ぶ直線
の中心を結ぶ直線![]() との交点を
との交点を![]() とする.
とする.
![]() から
から
![]() への接線の長さ
への接線の長さ
![]() に対して
に対して
![]() 上の点で
上の点で
以上の概念を準備すると平面の場合の諸定理が, 空間の反転と球の関連としてほぼそのまま成り立つ. すなわち,これまでに平面の反転をもとに示した次の諸定理は, 円を球になおしたうえで, 反転の中心と球の中心を含む平面を考えることで, 半径や中心間の距離の間の諸定理はすべて成立する. 共有点でのなす角のみは,一意ではないのでこのままでは意味をもたない. よって,
反転の基本性質を示す定理2は4)を除き成立.
ただし直交する二球,直線と球の直交という直交性は,
三次元の反転においても保たれる.
複比の定理3,
反転に関する不変量の定理4,
はすべて成立する.
また,
定理5は,円を球になおした命題「
互いに交わらない二球は,二球の焦点![]() を中心とする反転で
同心球にうつる.」で成立する.
を中心とする反転で
同心球にうつる.」で成立する.