


次: 楕円と円での場合
上: 特別な場合に閉形定理を計算で示す
前: 放物線と円,の場合
拓生
結局方法Bでやればいいのですね.
南海
その通り.円と円の場合も次のように考えよう.
例 1.7.5
拓生
やってみます.
解答
(1)
である.
つまり
 によって
によって
 ,
,
 と表される.
すべての実数に対して,
と表される.
すべての実数に対して,
 なので,
円
なので,
円 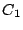 上の点は
上の点は  を除いて
を除いて
 と表される.
と表される.
 ,
,
 のとき直線
のとき直線 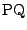 の方程式は
の方程式は

つまり
したがって直線 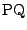 が円
が円 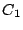 に接するための条件は
に接するための条件は
ゆえに求める  の条件は
の条件は
(2)
とおく.
となる.
拓生
 の係数が0でないことが確認できません.
の係数が0でないことが確認できません.
南海
除外点の考え方で次のようにしてはどうだろうか.
 の両辺を
の両辺を で割ると
で割ると
となる.ここで
 としたとき
としたとき
となるが,実数 に対して
に対して
 なので,
なので,
つまり
 .
.
拓生
わかりました.続けます.
 を
を の2次方程式と見たときその2解
の2次方程式と見たときその2解 は,
は,
である.このとき
なので
したがって
より
である. は因数分解できて,
は因数分解できて, は
は
と同値である.
これが となるために
となるために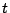 が満たすべき必要条件である.
が満たすべき必要条件である.
(3)
 を整理する.
を整理する.

ところが のもとでは
のもとでは
なので,
は実数解をもたない.
ところが少なくとも一つ となる点
となる点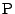 が存在した.
ゆえに(2)の条件式は恒等式であり,
が存在した.
ゆえに(2)の条件式は恒等式であり,
 である.
である.
 なので
なので
である.
この条件は
あるいは
とも書ける.
このとき を除く任意の点
を除く任意の点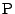 に対して(2)の条件式が成立し,
に対して(2)の条件式が成立し, となる.
となる.
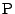 が連続的に変化すれば
が連続的に変化すれば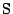 も連続的に変化する.
ゆえに
も連続的に変化する.
ゆえに を除く任意の点
を除く任意の点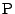 に対して
に対して となるなら,
となるなら,
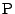 が
が のときも
のときも となる.□
となる.□
南海
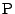 が
が のときは,上のようにいってもよいし,個別に調べてもよい.
のときは,上のようにいってもよいし,個別に調べてもよい.
また,「パスカルの定理」で勉強したように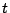 を無限遠点を加えた射影直線にとれば,
先の論証が
を無限遠点を加えた射影直線にとれば,
先の論証が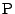 が
が のときも含んで成り立つこともわかる.
のときも含んで成り立つこともわかる.
以下,一つの除外点については特に断る必要はない.



次: 楕円と円で の場合
上: 特別な場合に閉形定理を計算で示す
前: 放物線と円,の場合
Aozora Gakuen
の場合
上: 特別な場合に閉形定理を計算で示す
前: 放物線と円,の場合
Aozora Gakuen
![]() は
は ![]() を満たす正の定数とする.
を満たす正の定数とする.
![]() 平面の二つの円
平面の二つの円
![]() がある.
定数は条件
がある.
定数は条件![]() を満たしているとする.
を満たしているとする.
![]() 上の一点
上の一点 ![]() から
から ![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
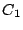 上の点
上の点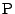 は,
は,
 を除き
を除き
 と媒介変数表示できることを示せ.
また,
と媒介変数表示できることを示せ.
また,
 ,
,
 とするとき,直線
とするとき,直線 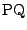 が
が 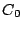 と接するための
と接するための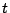 と
と に関する条件を求めよ.
に関する条件を求めよ.
 となるために
となるために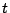 が満たすべき必要条件を求めよ.
が満たすべき必要条件を求めよ.
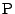 で
で となれば,
任意の点
となれば,
任意の点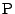 で
で となることを示せ.
となることを示せ.


 によって
によって
 ,
,
 と表される.
すべての実数に対して,
と表される.
すべての実数に対して,
 なので,
円
なので,
円  と表される.
と表される.

![\begin{eqnarray*}
T(s,\,t)&=&\{(r-a)st+r+a\}^2-(st-1)^2-(s+t)^2\\
&=&
[\{(r-a)^2-1\}t^2-1]s^2+2(r^2-a^2)ts+(r+a)^2-t^2-1
\end{eqnarray*}](images/img769.png)
![\begin{eqnarray*}
(s_1+s_2)^2+(s_1s_2-1)^2
&=&\dfrac{4(r^2-a^2)^2t^2+\{(r+a)^2-(...
...}\\
&=&\dfrac{\{(r+a)^2+(r-a)^2t^2\}^2}{[\{(r-a)^2-1\}t^2-1]^2}
\end{eqnarray*}](images/img781.png)
![\begin{eqnarray*}
H(t)&=&<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]>^2\\
&&\quad \quad -\{(r+a)^2+(r-a)^2t^2\}^2
\end{eqnarray*}](images/img782.png)
![\begin{eqnarray*}
&&(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]\\
&=&\pm\{(r+a)^2+(r-a)^2t^2\}
\end{eqnarray*}](images/img784.gif)
