南海
それでは次に円と楕円の場合に進もう.
東大の過去問もあるので![]() の場合だけではなく
の場合だけではなく![]() の場合も考えたい.
の場合も考えたい.
![]() の場合は基本的には円と円の場合と同様だ.
の場合は基本的には円と円の場合と同様だ.
![]() 平面の円と楕円
平面の円と楕円
 がある.
がある.
定数は条件![]() を満たしているとする.
を満たしているとする.
![]() 上の一点
上の一点 ![]() から
から ![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
 と媒介変数表示できることを示せ.
と媒介変数表示できることを示せ.
また,
 ,
Q
,
Q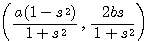 とするとき,直線
とするとき,直線 ![]() が
が ![]() と接するための
と接するための![]() と
と![]() に関する条件を求めよ.
に関する条件を求めよ.
拓生
これもできそうです.
解答
(1)
楕円 ![]() 上の点の座標は
上の点の座標は 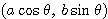 と表されるので, これを
と表されるので, これを ![]() で表すと,
で表すと,




これが円 ![]() と接するための必要十分条件は, 原点とこの直線との距離が1になる
ことであるから,求める必要十分条件は
と接するための必要十分条件は, 原点とこの直線との距離が1になる
ことであるから,求める必要十分条件は
(2)
ある実数 ![]() に対して, この方程式を
に対して, この方程式を ![]() についての方程式とみたときの
解
についての方程式とみたときの
解 ![]() が,
が, ![]() から円
から円 ![]() に引いた接線が
に引いた接線が ![]() と交わった
ときの
と交わった
ときの ![]() 上の点
上の点 ![]() を与える.
を与える.
ここで(2)の条件式を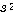 で割る.
で割る.
したがって ![]() は
は![]() の二次方程式で,
の二次方程式で,
![]() がその2解となるので, 解と係数の関係より,
がその2解となるので, 解と係数の関係より,
![]() が満たすべき条件は円と円の場合と同様に
が満たすべき条件は円と円の場合と同様に
ところで,






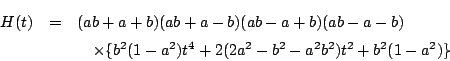
(3)
![]() のとき,
のとき,![]() を
を![]() の二次式と見たときの軸は
の二次式と見たときの軸は
ところが少なくとも一つ![]() となる点
となる点![]() が存在した.
ゆえに(2)の条件式は恒等的に0でなければならず,
が存在した.
ゆえに(2)の条件式は恒等的に0でなければならず,
