上: 代数分野

解答

解答 1   問題1

1. $$\begin{eqnarray*} A^2&=&tA+A(A-tE)\ =\ tA+\matrix{p}{q}{r}{s}\matrix{-s}{q}{r}{-p}\\ &=&tA+\matrix{-ps+qr}{0}{0}{-ps+qr}\ =\ tA-dE \end{eqnarray*}$$
   
   

2. $$\begin{eqnarray*} a_{n+1}A+b_{n+1}E&=&A^{n+1}\ =\ AA^n\ =\ A(a_nA+b_nE)\\ &=&a_nA^2+b_nA\ =\ (ta_n+b_n)A-da_nE \end{eqnarray*}$$
   
   
   
   
   $$∴\quad(a_{n+1}-ta_n-b_n)A=-(b_{n+1}+da_n)E$$
   
   
   ここで, $a_{n+1}-ta_n-b_n\ne0$ なら, $A=\dfrac{-(b_{n+1}+da_n)}{a_{n+1}-ta_n-b_n}E$ となるので仮定に反する. したがって
   
   $$a_{n+1}-ta_n-b_n=0,\ b_{n+1}+da_n=0\qquad∴\quad\left\{\begin{array}{l} a_{n+1}=ta_n+b_n\\ b_{n+1}=-da_n \end{array}\right.$$
   
   

3. $A=\matrix{-1}{-2}{3}{4}$ のとき, $t=3,\ d=2$ である. つまり
   
   $$\left\{\begin{array}{ll} a_{n+1}=3a_n+b_n&\cdots\maru1\\ b_{n+1}=-2a_n&\cdots\maru2 \end{array}\right.$$
   
   
   $\maru1+\maru2$ から
   
   $$a_{n+1}+b_{n+1}=a_n+b_n\qquad∴\quad a_n+b_n=a_1+b_1=1+0$$
   
   
   $b_n=1-a_n$ を1に代入する.
   
   $$\begin{array}{c} a_{n+1}=3a_n+1-a_n=2a_n+1\quad\iff\quad a_{... ...rray}{l} a_n=2^n-1\\ b_n=-2^n+2 \end{array}\right. \end{array}$$
   
   
   よって
   $$\begin{eqnarray*} A^n&=&(2^n-1)\matrix{-1}{-2}{3}{4}+(-2^n+2)\matrix{1}{0}{0}{1}... ...&=&\matrix{-2\cdot2^n+3}{-2\cdot2^n+2}{3\cdot2^n-3}{3\cdot2^n-2} \end{eqnarray*}$$
   
   

解答 2   問題2

1. $$\begin{eqnarray*} x^{n+1}&=&x^n\cdot x\\ &=&\{(x^2-x+d)Q_n(x)+a_nx+b_n\}\cdot x... ...+a_n\}+a_nx+b_nx-da_n\\ &=&(x^2-x+d)Q_{n+1}(x)+a_{n+1}x+b_{n+1} \end{eqnarray*}$$
   
   
   よって, $n=1,\,2,\,3,\,\cdots$ に対して, $a_{n+1}=a_n+b_n,\ b_{n+1}=-da_n$ が成り立つ.
2. $n=1$ のときは $a_1=1,\ b_1=0$ より成立.
   $A^n=a_nA+b_nE$ とする．このとき
   $$\begin{eqnarray*} A^{n+1}&=&A(a_nA+b_nE)\ =\ a_nA^2+b_nA\\ &=&a_n(A-dE)+b_nA\ =\ (a_n+b_n)A-da_nE\\ &=&a_{n+1}A+b_{n+1}E \end{eqnarray*}$$
   
   
   よって, 帰納法により自然数 $n$ に対して $A^n=a_nA+b_nE$

   別解1

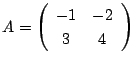   $n=1$ のときは上と同様.
   $n=2$ のとき, $a_2=1+0=1,\ b_2=-d$ . つまり, $A^2=A-dE$ でなければならない．一方 $A^2-A+dE=O$ より, $A^2=A-dE=O$ なので成立.
   $n,\ n+1$ で成立するとする.
   $A^2-A+dE=O$ より, $A^{n+2}-A^{n+1}+dA^n=O$ ．よって

   $$\begin{eqnarray*} A^{n+2}&=&A^{n+1}-dA^n\ =\ a_{n+1}A+b_{n+1}E-d(a_nA+b_nE)\\ &... ...n+b_n)E\ =\ (a_{n+1}+b_{n+1})A-da_{n+1}E\\ &=&a_{n+2}A+b_{n+2}E \end{eqnarray*}$$
   
   
   よって, 帰納法により自然数 $n$ に対して, $A^n=a_nA+b_nE$

   別解2

   $(aA^n)(bA^m)=abA^{n+m}$ なので行列 $A$ の多項式の積は文字の場合の展開と同様にできる.
   よって，恒等式 $f(x)=g(x)$ に対して $f(A)=g(A)$ が成り立つ.
   したがって, $x^n=(x^2-x+d)Q_n(x)+a_nx+b_n$ より
   

   $$A^n=a_nA+b_nE$$
   
   

3. ケイレイ・ハミルトンの定理から
   
   $$A^2-(1+0)A+(1\cdot0-2\cdot3)E=A^2-A-6E=O$$
   
   
   
   
   $$x^n=(x^2-x-6)Q_n(x)+a_nx+b_n=(x-3)(x+2)Q_n(x)+a_nx+b_n$$
   
   
   ここで, $x=3,\ x=-2$ を代入する.
   
   $$3^n=a_n\cdot3+b_n,\quad(-2)^n=a_n\cdot(-2)+b_n$$
   
   
   これから
   
   $$a_n=\dfrac{3^n-(-2)^n}{5},\quad b_n=\dfrac{2\cdot3^n+3(-2)^n}{5}$$
   
   
   よって, (2)から
   $$\begin{eqnarray*} A^n&=&a_nA+b_nE\\ &=&\dfrac{3^n-(-2)^n}{5}\matrix{1}{2}{3}{0}... ...n}{5}}{\dfrac{2\cdot3^n+3(-2)^n}{5}}\\ &&(n=1,\,2,\,3,\,\cdots) \end{eqnarray*}$$
   
   

解答 3   問題3

1. $\vecarray{f_n}{f_{n+1}}=\matrix{0}{1}{2}{1}\vecarray{f_{n-1}}{f_n}$ より, $A=\matrix{0}{1}{2}{1}$ とすればよい.
2. $\matrix{0}{1}{2}{1}\vecarray{1}{x}=k\vecarray{1}{x}$ とおく.
   $\matrix{-k}{1}{2}{1-k}\vecarray{1}{x}=O$ が $\vecarray{1}{x}=O$ 以外の解をもつので
   
   $$\Delta\matrix{-k}{1}{2}{1-k}=0\quad\Rightarrow\quad k^2-k-2=0\qquad∴\quad k=2,\ -1$$
   
   
   
   
   $$\left\{\begin{array}{lll} k=2のとき &\matrix{-2}{1}{2}{-1}\v... ...ix{1}{1}{2}{2}\vecarray{1}{x}=O\,より,&x=-1 \end{array}\right.$$
   
   
   
   
   $$∴\quad a=2,\ b=-1,\ u=2,\ v=-1$$
   
   

3. $AP=P\matrix{2}{0}{0}{-1}$ となるので
                                            $P^{-1}AP=\matrix{2}{0}{0}{-1}$
4. $\vecarray{f_n}{f_{n+1}}=A\vecarray{f_{n-1}}{f_n}=A^{n-1}\vecarray{f_1}{f_2}$ である．ここで
   
   $$\begin{array}{c} \left(P^{-1}AP\right)^{n-1}=\matrix{2}{0}{0... ...n-1}P\quad\iff\quad A^{n-1}=P(P^{-1}AP)^{n-1}P^{-1} \end{array}$$
   
   
   $$\begin{eqnarray*} ∴\quad\vecarray{f_n}{f_{n+1}} &=&A^{n-1}\vecarray{f_1}{f_2}\ ... ...ix{1}{1}{2}{-1}\vecarray{2^{n-1}(f_1+f_2)}{(-1)^{n-1}(2f_1-f_2)} \end{eqnarray*}$$
   
   
   よって
   
   $$f_n=\dfrac{1}{3}\{2^{n-1}+2\cdot(-1)^{n-1}\}f_1+\dfrac{1}{3}\{2^{n-1}-(-1)^{n-1}\}f_2$$
   
   

解答 4   問題4

1. $$\begin{eqnarray*} \alpha u_{n+3}+\beta v_{n+3} &=&\alpha(u_n+u_{n+1}+u_{n+2})+... ...(\alpha u_{n+1}+\beta v_{n+1}) +(\alpha u_{n+2}+\beta v_{n+2}) \end{eqnarray*}$$
   
   
   つまり，数列 $\{ \alpha u_n+\beta v_n \}$ は性質 (F) を持つ.
2. 
   
   $$\alpha=y_1,\ \beta=y_2,\ \gamma=y_3$$
   
   
   とおく．このとき
   
   $$y_n=\alpha a_n+\beta b_n+\gamma c_n$$
   
   
   となることを数学的帰納法で示す．

   $n=1,\ 2,\ 3$ については 数列 $\{ a_n \},\ \{b_n\},\ \{c_n\}$ の条件から成立する．

   $n,\ n+1,\ n+2$ で成立したとする．

   $$\begin{eqnarray*} y_{n+3}&=&y_n+y_{n+1}+y_{n+2}\\ &=&(\alpha a_n+\beta b_n+\g... ...+1}+c_{n+2})\\ &=&\alpha a_{n+3}+\beta b_{n+3}+\gamma c_{n+3} \end{eqnarray*}$$
   
   
   ゆえに $n+3$ でも成立し，帰納法によってすべての $n$ で成立する．
3. ある実数 $\alpha,\ \beta,\ \gamma$ を選んで
   
   $$h_n=\alpha d_n+\beta e_n+\gamma f_n$$
   
   
   と表すことができたとする．
   $$\begin{eqnarray*} (h_1,\ h_2,\ h_3) &=&(\alpha d_1+\beta e_1+\gamma f_1,\ \alp... ...d_1,\ d_2,\ d_3)+\beta(e_1,\ e_2,\ e_3)+\gamma(f_1,\ f_2,\ f_3) \end{eqnarray*}$$
   
   
   つまり空間ベクトルの間に
   
   $$(1,\ 1,\ 1)=\alpha(0,\ 1,\ 1)+\beta(1,\ 1,\ 0)+\gamma(1,\ 0,\ -1)$$
   
   
   という関係がある． ところが $(1,\ 0,\ -1)=(1,\ 1,\ 0)-(0,\ 1,\ 1)$ なので
   
   $$(1,\ 1,\ 1)=(\alpha-\gamma)(0,\ 1,\ 1)+(\beta+\gamma)(1,\ 1,\ 0)$$
   
   
   つまり
   
   $$1=\beta+\gamma,\ 1=\alpha+\beta,\ 1=\alpha-\gamma$$
   
   
   ところが第1式と第3式から $2=\alpha+\beta$ となり，第2式と矛盾した．

   ゆえにどのように $\alpha,\ \beta,\ \gamma$ を選んでも 数列 $\{ h_n \}$ を 題意のように表すことはできない

解答 5   問題5

1. 行列 $xE-A=\matrix{x-4}{-3}{-2}{x+1}$が逆行列をもたないので
   
   $${\it\Delta}(xE-A)=(x-4)(x+1)-6=x^2-3x-10=(x-5)(x+2)=0$$
   
   
   したがって $\alpha=5,\ \beta=-2$である．よって
   
   $$P=\dfrac{1}{7}\matrix{6}{3}{2}{1},\ Q=-\dfrac{1}{7}\matrix{-1}{3}{2}{-6}$$
   
   
   $$\begin{eqnarray*} PQ&=&-\dfrac{1}{49}\matrix{6}{3}{2}{1}\matrix{-1}{3}{2}{-6}\\ &=&-\dfrac{1}{49}\matrix{0}{0}{0}{0}=\matrix{0}{0}{0}{0} \end{eqnarray*}$$
   
   

2. $$\begin{eqnarray*} P^2&=&\dfrac{1}{7^2}\matrix{6}{3}{2}{1}^2\\ &=&\dfrac{1}{49}\matrix{42}{21}{14}{7}=P \end{eqnarray*}$$
   
   
   この等式の両辺に$P^n$を乗じて
   
   $$P^{n+1}=P^n$$
   
   
   
   
   $$∴\quad P^n=P=\dfrac{1}{7}\matrix{6}{3}{2}{1}$$
   
   

3. 
   
   $$A^n=\alpha^nP+\beta^nQ$$
   
   
   を数学的帰納法で示す．

   $n=1$のとき．

   $$\begin{eqnarray*} \alpha P+\beta Q&=&\dfrac{5}{7}\matrix{6}{3}{2}{1}+ \dfrac{2... ...trix{-1}{3}{2}{-6}\\ &=&\dfrac{1}{7}\matrix{28}{21}{14}{-7}=A \end{eqnarray*}$$
   
   
   より成立．

   $n=k$のとき $A^k=\alpha^kP+\beta^kQ$とする．(1)と同様に$QP=O$でもある．

   $$\begin{eqnarray*} ∴\quad A^{k+1}&=&(\alpha^kP+\beta^kQ)(\alpha P+\beta Q)\\ ... ...alpha\beta^kQP+\beta^{k+1}Q^2\\ &=&\alpha^{k+1}P+\beta^{k+1}Q \end{eqnarray*}$$
   
   
   よって$n=k+1$でも成立し，題意が示された．

別解

※上の計算では単に計算するだけなので，もう少しなぜこのようになるのかわかるように証明しておく． 冒頭の部分は同じ．

1. 解と係数の関係から $\alpha+\beta=3,\ \alpha\beta=-10$である．
   $$\begin{eqnarray*} PQ&=&-\dfrac{1}{\beta^2-\alpha^2}\matrix{\alpha+1}{3}{2}{\alp... ...rac{1}{\beta^2-\alpha^2}\matrix{0}{0}{0}{0}=\matrix{0}{0}{0}{0} \end{eqnarray*}$$
   
   

2. $$\begin{eqnarray*} P+Q&=& \dfrac{1}{\alpha-\beta}\matrix{\alpha+1}{3}{2}{\alpha... ...rac{1}{\beta-\alpha}\matrix{\beta-\alpha}{0}{0}{\beta-\alpha}=E \end{eqnarray*}$$
   
   
   である．したがって
   
   $$P^2=P(E-Q)=P-PQ=P$$
   
   

   ゆえに本解と同様に$P^n=P$である．

3. 
   
   $$QP=(E-P)P=P-P^2=O$$
   
   
   も同様である．

   ここで

   $$\begin{eqnarray*} \alpha P+\beta Q&=&\dfrac{\alpha}{\alpha-\beta}\matrix{\alpha... ...4\alpha}\\ &=&\matrix{\beta+\alpha+1}{3}{2}{\beta+\alpha-4}=A \end{eqnarray*}$$
   
   
   $PQ=QP=O$なので
   $$\begin{eqnarray*} A^n&=&(\alpha P+\beta Q)^n\\ &=&(\alpha P+\beta Q)(\alpha P... ... Q)\\ &=&\alpha^n P^n+\beta^n Q^n\\ &=&\alpha^n P+\beta^n Q \end{eqnarray*}$$
   
   

解答 6       問題6 $f$はベクトル $x\mathrm{\bf e}_1+y\mathrm{\bf e}_2$を

$$f\left(x\mathrm{\bf e}_1+y\mathrm{\bf e}_2\right)= x\vecarray{3}{4}+y\vecarray{2}{1}=\vecarray{3x+2y}{4x+y}$$

に写す．$f$は成分の変換としては行列 $\left( \begin{array}{cc} 3&2\\ 4&1 \end{array}\right)$ で表される．よって$f^{-1}$は成分の変換としては

$$\left( \begin{array}{cc} 3&2\\ 4&1 \end{array}\right)^{... ...} \left( \begin{array}{cc} 1&-2\\ -4&3 \end{array}\right)$$

で表される．つまり，$f^{-1}$は

$$f(\mathrm{\bf e}_1)=\dfrac{-1}{5}\vecarray{1}{-4},\ f(\mathrm{\bf e}_2)=\dfrac{-1}{5}\vecarray{-2}{3}$$

で定まる線型写像である．

解答 7       問題7

(1) $A=\matrix{1}{-1}{2}{4}$とおく．

$$\left(\mathrm{\bf e}_1,\ \mathrm{\bf e}_2 \right) \left( \b... ...{array}\right) =\left(\vecarray{1}{2},\ \vecarray{1}{1}\right)$$

より $P=\left( \begin{array}{cc} 1&1\\ 2&1 \end{array}\right)$である．よって$f$をこの基底で表すと対応する行列は

$$P^{-1}AP=-\matrix{1}{-1}{-2}{1}\matrix{1}{-1}{2}{4}\matrix{1}{1}{2}{1} =\matrix{11}{6}{-8}{-6}$$

(2) $P=\left( \begin{array}{cc} 1&1\\ -1&-2 \end{array}\right)$である．よって$f$をこの基底で表すと対応する行列は

$$P^{-1}AP=-\matrix{2}{1}{-1}{-1}\matrix{1}{-1}{2}{4} \matrix{2}{1}{-1}{-1} =\matrix{3}{9}{0}{-9}$$

解答 8       問題8

(1) $P=\left( \begin{array}{cccc} 1&0&0&0\\ 0&0&1&0\\ 0&1&0&0\\ 0&0&0&1 \end{array}\right)$で$P^2=E$なので，求める行列は

$$\left( \begin{array}{cccc} 1&0&0&0\\ 0&0&1&0\\ 0&1&0&0... ...&2&2\\ 2&3&1&-1\\ -1&3&0&1\\ 1&3&1&1 \end{array}\right)$$

(2) $P=\left( \begin{array}{cccc} 1&1&1&1\\ 0&1&1&1\\ 0&0&1&1\\ 0&0&0&1 \end{array}\right)$である． $P^{-1}=\left( \begin{array}{cccc} 1&-1&0&0\\ 0&1&-1&0\\ 0&0&1&-1\\ 0&0&0&1 \end{array}\right)$なので，求める行列は

$$\left( \begin{array}{cccc} 1&-1&0&0\\ 0&1&-1&0\\ 0&0&1... ...5&6\\ -3&-1&0&2\\ 1&0&0&-4\\ 1&2&5&8 \end{array}\right)$$

解答 9       問題9

1. 
   
   $$\begin{array}{ll} \quad \left\vert \begin{array}{ccc} a_... ...t\vert&\\ =a_1b_3(a_2b_1-a_1b_2)(a_3b_2-a_2b_3) \end{array}$$
   
   
   一般化
   
   $$\left\vert \begin{array}{ccccc} a_1b_1&a_1b_2&a_1b_3&…&a... ...rray} \right\vert=a_1b_n\prod_{i=2}^n(a_i2b_{i-1}-a_{i-1}b_i)$$
   
   

2. $$\begin{eqnarray*} &&\left\vert \begin{array}{ccc} 1&1&1\\ {}_1\mathrm{C}_1&... ...0\\ 0&1&1\\ 0&1&{}_2\mathrm{C}_1 \end{array} \right\vert=1 \end{eqnarray*}$$
   
   
   一般化
   
   $$\left\vert \begin{array}{ccccc} 1&1&1&…&1\\ {}_1\mathr... ...hrm{C}_n &…&{}_{2n} \mathrm{C}_n \end{array} \right\vert=1$$
   
   
   ※    この式の値を$D_n$とすると， $D_n=D_{n-1}$となり示せる．
3. 左辺の$x_i$に$x_j$を代入すれば行列式は0になる． よって左辺は$x_i-x_j$で割りきれる． 左辺は $(x_1-x_2)(x_2-x_3)(x_1-x_3)$で割りきれる． $x_1^2x_2$の係数比較から
   
   $$左辺=-(x_1-x_2)(x_2-x_3)(x_1-x_3)$$
   
   
   一般化
   
   $$\left\vert \begin{array}{ccccc} 1&x_1&{x_1}^2&…&{x_1}^{n... ...rray} \right\vert=(-1)^{\frac{n(n-1)}{2}}\prod_{i<j}(x_i-x_j)$$
   
   
   これを「Vandermonde の行列式」という．

解答 10       問題10

（１）     最小多項式は

$$t^2-4t-1$$

である．$t^2-4t-1=0$の2根は$2\pm\sqrt{5}$である． $t^8$を最小多項式で割った余りを$pt+q$とする．

$$t^8=(t^2-4t-1)Q(t)+pt+q$$

とおく．

$$(2\pm\sqrt{5})^8=p(2\pm\sqrt{5})+q$$

より

$$p=\dfrac{(2+\sqrt{5})^8-(2-\sqrt{5})^8}{2\sqrt{5}},\ \quad q=\dfrac{(2+\sqrt{5})^7-(2-\sqrt{5})^7}{2\sqrt{5}}$$

$$A^8=pA+qE=\dfrac{(2+\sqrt{5})^8-(2-\sqrt{5})^8}{2\sqrt{5}} \... ...{5}} \left( \begin{array}{cc} 1&0\\ 0&1 \end{array}\right)$$

（２）     最小多項式は$t^3-2t^2+t$．

$$t^8=(t^3-2t^2+t)Q(t)+pt^2+qt+r$$

とおく． $t^3-2t^2+t=t(t-1)^2$から$t=0,\ 1$を代入し， さらに微分して$t=1$を代入することにより，余りは$7t^2-6t$である．

$$B^8=7B^2-6B=(7B-6E)B=\left( \begin{array}{ccc} 24&45&66\\ -22&-41&-60\\ 7&13&19 \end{array}\right)$$

解答 11       問題11

（１）     特性方程式は

$$(t-1)(t^2+1)=0$$

となり，固有値は$1,\ i,\ -i$である．それぞれ固有ベクトルを求める．

$t=1$のとき，

$$A-E=\left( \begin{array}{ccc} 0&2&2\\ 1&-2&1\\ 4&-12&0 \end{array}\right)$$

これから

$$\left\{ \begin{array}{l} 2y+2z=0\\ x-2y+z=0\\ 4x-12y=0 \end{array}\right.$$

$x$と$y$について解いて

$$x=-3z,\ y=-z$$

対応する固有ベクトル次のもにとる．

$$\mathrm{\bf u}_1= \left( \begin{array}{c} 3\\ 1\\ -1 \end{array}\right)$$

$t=\pm i$のとき，

$$A \mp iE=\left( \begin{array}{ccc} 1\mp i&2&2\\ 1&-1\mp i&1\\ 4&-12&1\mp i \end{array}\right)$$

これから

$$\left\{ \begin{array}{l} (1\mp i)x+2y+2z=0\\ x-(1\pm i)y+z=0\\ 4x-12y+(1\mp i)z=0 \end{array}\right.$$

$x$と$y$について解いて

$$x=\dfrac{-2\mp i}{2}z,\ y=\dfrac{-1\mp i}{4}z$$

対応する固有ベクトル次のもにとる．

$$\mathrm{\bf u}_2,\ \mathrm{\bf u}_3= \left( \begin{array}{c} 4\pm 2i\\ 1 \pm i\\ -4 \end{array}\right)$$

変換行列として

$$P=\left(\mathrm{\bf u}_1,\ \mathrm{\bf u}_2,\ \mathrm{\bf u}... ...c} 3&4+2i&4-2i\\ 1&1+i&1-i\\ -1&-4&-4 \end{array}\right)$$

このとき標準形は

$$P^{-1}AP= \left( \begin{array}{ccc} 1&0&0\\ 0&i&0\\ 0&0&-i \end{array}\right)$$

である．

（２）     特性方程式を Asir で因数分解すると

	[0] B-tE=newmat(3,3,[[-4-t,9,-4],[-9,18-t,-8],[-15,29,-13-t]]);
	[ -t-4 9 -4 ][ -9 -t+18 -8 ][ -15 29 -t-13 ]
	[1] fctr(det(B));
	[[-1,1],[t-1,2],[t+1,]]

特性方程式は

$$(t-1)^2(t+1)=0$$

となり，固有値は $1\ (重根),\ -1$である．

$t=-1$のとき． $B+E= \left( \begin{array}{ccc} -3&9&-4\\ -9&19&-8\\ -15&29&-12 \end{array}\right)$である． 対応する固有ベクトルを次のもにとる．

$$\mathrm{\bf u}_1= \left( \begin{array}{c} 1\\ 3\\ 6 \end{array}\right)$$

$t=1$のとき． $B-E= \left( \begin{array}{ccc} -5&9&-4\\ -9&17&-8\\ -15&29&-14 \end{array}\right)$で，また Asir で計算すると， $(B-E)^2= \left( \begin{array}{ccc} 4&-8&4\\ 12&-24&12\\ 24&-48&24 \end{array}\right)$である．これから

$$\mathrm{\bf u}_2= \left( \begin{array}{c} 1\\ 1\\ 1 \... ...= \left( \begin{array}{c} a\\ 0\\ -a \end{array}\right)$$

としてみる．

$$Q=\left(\mathrm{\bf u}_1,\ \mathrm{\bf u}_2,\ \mathrm{\bf u}... ...in{array}{ccc} 1&1&a\\ 3&1&0\\ 6&1&-a \end{array}\right)$$

とする．

$$Q^{-1}=\dfrac{1}{a}\left( \begin{array}{ccc} a&-2a&a\\ -3a&7a&-3a\\ 3&-5&2 \end{array}\right)$$

となる．

$$Q^{-1}BQ= \left( \begin{array}{ccc} -1&0&0\\ 0&1&-a\\ 0&0&1 \end{array}\right)$$

となるので，$a=-1$にとる．つまり変換行列を $Q=\left( \begin{array}{ccc} 1&1&-1\\ 3&1&0\\ 6&1&1 \end{array}\right)$とするとき標準形は次のものになる．

$$Q^{-1}BQ=\left( \begin{array}{ccc} -1&0&0\\ 0&1&1\\ 0&0&1 \end{array}\right)$$

上: 数列と行列 前: 直交変換と直交行列