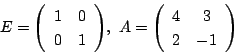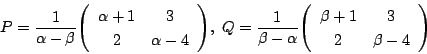行列
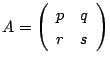 に対して,
に対して,
![]() とおく.このとき,次の問いに答えよ.ただし,
とおく.このとき,次の問いに答えよ.ただし, ![]() は二次の単位行列であり,
は二次の単位行列であり, ![]() となる実数
となる実数 ![]() は存在しないものとする.
は存在しないものとする.
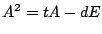 となることを示せ.
となることを示せ.
-
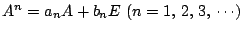 とする
とき,
とする
とき,
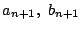 を
を
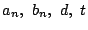 を用いて表せ.
を用いて表せ.
-
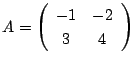 のとき,
のとき,
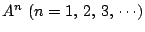 を求めよ.
を求めよ.
行列
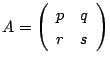 に対して,
に対して,
![]() とおく.このとき,次の問いに答えよ.ただし,
とおく.このとき,次の問いに答えよ.ただし, ![]() は二次の単位行列であり,
は二次の単位行列であり, ![]() となる実数
となる実数 ![]() は存在しないものとする.
は存在しないものとする.
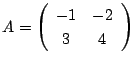 のとき,
のとき,
実数 ![]() を定数とし, 二次の正方行列
を定数とし, 二次の正方行列 ![]() は
は ![]() をみたすとする.また,自然数
をみたすとする.また,自然数
![]() に対して,
に対して, ![]() についての整式の
についての整式の ![]() を
を ![]() で割ったときの商を
で割ったときの商を ![]() , 余りを
, 余りを ![]() とする. すなわち,
とする. すなわち,
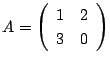 とする.このとき,
とする.このとき,
数列 ![]() は,
は,
![]() となる関係がある.
このとき,次の問いに答えよ.
となる関係がある.
このとき,次の問いに答えよ.
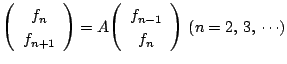 を
みたす行列
を
みたす行列 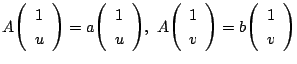 をみたす
をみたす 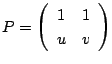 とする.
とする.
数列 ![]() が
が
行列 ![]() と
と![]() を
を