

 次: 整式と見るか整数と見るか
上: 整式と見るか関数と見るか
前: 関数値の符号[01慶応理工]
次: 整式と見るか整数と見るか
上: 整式と見るか関数と見るか
前: 関数値の符号[01慶応理工]
問題
次の実数係数の三次式を 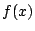 とする.
とする.
いま,二つの実数係数の整式 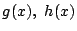 が次を満たすものとする.
が次を満たすものとする.
このとき次のいずれかが成り立つことを示せ.
-
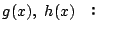 恒等的に等しい.
恒等的に等しい.
- 二つの整式
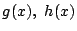 はともに定数である.
はともに定数である.
方針

解1
これがすべての 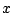 で成立するので,
で成立するので, 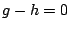 か
か
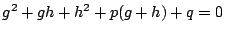 かのいずれかは無数の
かのいずれかは無数の 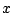 で成立する.
で成立する.
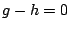 が無数の
が無数の 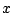 で成立するとすれば,
で成立するとすれば, 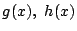 が
が 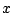 の整式なので
の整式なので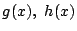 は恒等的に等しい.
同様に
は恒等的に等しい.
同様に
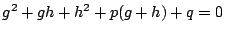 が無数の
が無数の 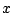 で成立し,したがって恒等的に成立するとする.
で成立し,したがって恒等的に成立するとする.
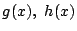 の次数が異なる場合,大きい方の次数を
の次数が異なる場合,大きい方の次数を 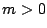 とすると
とすると
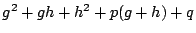 は
は 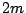 次の整式である.恒等的に0ではあり得ない.
次の整式である.恒等的に0ではあり得ない.
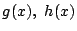 の次数が等しい場合,それを
の次数が等しい場合,それを 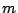 次として
次として
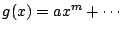 ,
,
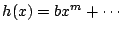 と置く.このとき
と置く.このとき
となる.
実数 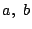 に対して
に対して 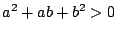 であるからもし
であるからもし 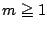 なら
これが恒等的に0になることはない.
なら
これが恒等的に0になることはない.
ゆえに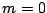 で,
で,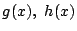 はともに定数である.□
はともに定数である.□
解2
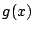 が定数でないとする.
が定数でないとする. 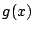 は実数係数の整式なので,
は実数係数の整式なので,
である.
これが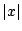 が十分大きいすべての
が十分大きいすべての 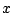 で成立する.
で成立する. 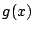 は整式なので,恒等的に成立する.
は整式なので,恒等的に成立する.
次に
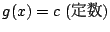 とする.
とする.
したがって 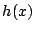 はすべての
はすべての 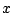 に対して
に対して
 次方程式
次方程式
の解にいずれかに一致しなければならない.実数解は有限個なので
少なくとの一つの解で,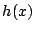 が一致するような
が一致するような 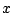 が無数にあるものがある.
が無数にあるものがある.
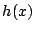 は整式なので,恒等的にこの解に等しい,つまり
は整式なので,恒等的にこの解に等しい,つまり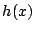 も定数である.□
も定数である.□
吟味
解2のように考えると,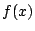 は任意の実数係数の整式で成立することがわかる.大切なことなので,恒等式の定義を書いておこう.
は任意の実数係数の整式で成立することがわかる.大切なことなので,恒等式の定義を書いておこう.
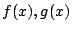 が
が 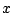 についての整式であるとき,次の3つの命題は同値である.
またこのとき,等式
についての整式であるとき,次の3つの命題は同値である.
またこのとき,等式 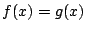 は 恒等式 であるという.
2式の次数の小さくない方を
は 恒等式 であるという.
2式の次数の小さくない方を とする.
とする.
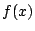 と
と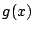 は同一の式である.つまり,次数が等しくかつ同じ次数の項の係数が等しい.
は同一の式である.つまり,次数が等しくかつ同じ次数の項の係数が等しい.
- 任意の
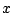 の値に対して
の値に対して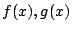 は同一の値をとる.
は同一の値をとる.
- 等式
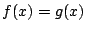 が異なる
が異なる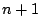 個の
個の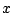 の値に対して成り立つ.
の値に対して成り立つ.
証明
-
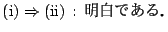
-
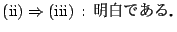
-
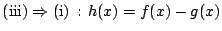 は
は
 次以下の整式である.
次以下の整式である.
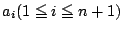 のあい異なる
のあい異なる 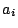 に対して,
に対して,
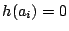 であるから,因数定理より,
であるから,因数定理より,
と因数分解される.
もし 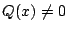 なら,左辺の次数は
なら,左辺の次数は  以下であり,
右辺の次数は
以下であり,
右辺の次数は 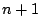 以上となる.よって矛盾が起こる.
従って
以上となる.よって矛盾が起こる.
従って 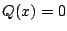 となり
となり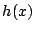 は式として0である.
は式として0である.
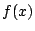 と
と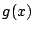 は同一の式である.
は同一の式である.
3つの条件は互いに他の2つの必要十分条件になっていることが示されているので,
題意が示された.□



次: 整式と見るか整数と見るか
上: 整式と見るか関数と見るか
前: 関数値の符号[01慶応理工]
Aozora Gakuen
![]() とする.
とする.

![]() の次数が異なる場合,大きい方の次数を
の次数が異なる場合,大きい方の次数を ![]() とすると
とすると
![]() は
は ![]() 次の整式である.恒等的に0ではあり得ない.
次の整式である.恒等的に0ではあり得ない.
![]() の次数が等しい場合,それを
の次数が等しい場合,それを ![]() 次として
次として
![]() ,
,
![]() と置く.このとき
と置く.このとき
![]() で,
で,![]() はともに定数である.□
はともに定数である.□
![]() が定数でないとする.
が定数でないとする. ![]() は実数係数の整式なので,
は実数係数の整式なので,

![]() とする.
とする.
![]() は整式なので,恒等的にこの解に等しい,つまり
は整式なので,恒等的にこの解に等しい,つまり![]() も定数である.□
も定数である.□
![]() は任意の実数係数の整式で成立することがわかる.大切なことなので,恒等式の定義を書いておこう.
は任意の実数係数の整式で成立することがわかる.大切なことなので,恒等式の定義を書いておこう.
![]() が
が ![]() についての整式であるとき,次の3つの命題は同値である.
またこのとき,等式
についての整式であるとき,次の3つの命題は同値である.
またこのとき,等式 ![]() は 恒等式 であるという.
2式の次数の小さくない方を
は 恒等式 であるという.
2式の次数の小さくない方を![]() とする.
とする.