次: 塗り分け［99京大文系］ 上: 直接計算か漸化式か 前: 階段の昇り方［07京大理系］

一筆がき［08京大文系］

このような別解はさらに複雑な場合にも可能である．

問題     

正$n$角形とその外接円を合わせた図形を$F$とする，$F$上の点Pに対して， 始点と終点がともにPであるような，図形$F$の一筆がきの経路の数を$N(\mathrm{P})$で表す． 正$n$角形の頂点をひとつとってAとし， $a=N(\mathrm{A})$とおく． また正$n$角形の辺をひとつとってその中点をBとし， $b=N(\mathrm{B})$とおく．このとき$a$と$b$を求めよ．

注：一筆がきとは，図形を，かき始めから終わりまで，筆を紙からはなさず， また同じ線上を通らずにかくことである．

方針

1.

直接数える． 直接数えるときは， $b=N(\mathrm{B})$は $a=N(\mathrm{A})$との関係を見極めるようにしよう．

2.

$n$のときの場合の数を$a_n$や$b_n$とおいて，漸化式を立てる．

解1
$a=N(\mathrm{A})$について． 一筆がきの経路に関する場合分けは次の様に起こる．

1. 頂点から隣りあう頂点への移動は$n$カ所あり， それぞれ移り方は辺と弧のいずれを先に通るかの2通り． したがって，頂点の間の移動の順を決めれば，それに対して経路は$2^n$通りできる．
2. 点の間の移動順では，右回りから始めるか，左回りから始めるかが場合分けされる． これは対称性からたがいに同数あるので，左回りからはじめる場合で考えその2倍ある．
3. 左回りからはじめるときで考える． 点の間の移動順では，途中で折り返さないか途中で折り返すか場合に分けられる． 折り返さない場合は1通り． 折り返す場合．2回折り返すのはA以外で折り返すとき．Aで折り返すときは1回折り返す． したがって折り返しなしも含めて，折り返しの仕方は$n+1$通り．

これらはそれぞれ異なる一筆がきを作り，場合分けは他にはない．

$$∴\quad a=2^n\cdot 2\cdot(n+1)=(n+1)2^{n+1}$$

$b=N(\mathrm{B})$について．

点Bのある辺をCDとする．反時計回りにC，B，Dと並ぶものとする．

点Bに始まり点Bに終わる一つの一筆がきに対し， 左回りなら最初のBDを書くところを最後に移動することでDから始まる一筆がきで， 最後にDに戻るとき辺を通るものが得られる． 右回りなら最初のBCを書くところを最後に移動することでCから始まる一筆がきで， 最後にCに戻るとき辺を通るものが得られる． 逆にこの操作を逆にたどることで，頂点を始点とする一筆がきで最後に始点に戻るとき辺を通るものから， その辺の中点を始点とする一筆がきが得られ，これは一対一に対応している．

したがって，$b$は頂点から始まる一筆がきで， 最後に始点に戻るとき辺を通ると指定した場合の数に等しい． この条件を付け加えた頂点を始点とする一筆がきは$a$の計算で(i)の部分を$2^{n-1}$としたものである．

$$∴\quad b=(n+1)2^n$$

解2
正$n$角形の代わりに凸な$n$角形で考えても同じことである．

$n$角形のときの$a$を$a_n$とする． $n=3$のとき， 左回りと決めると$a_3$は点の移動の順番の決め方が4通りある． 一つの順番に対し，辺と弧の選び方は$2^3$通りある． 右回りも同数． ゆえに $a_3=2\cdot4\cdot2^3=64$である．

$n$角形に新たに$n+1$番の頂点を加えると， その頂点を挟むもとの$n$角形の2頂点の間の移動の仕方が， 2通りから4通りになる． これによって$n$角形の場合の一つの一筆がきの経路に対し， $n+1$角形の場合の一筆がきの経路が2つ得られる．

さらに新たに付け加わった$n+1$番目の点で折り返す一筆がきの経路が 右回りと左回りも考えて$2\cdot2^{n+1}$個できる． ゆえに

$$a_{n+1}=2a_n+2\cdot2^{n+1}$$

これから

$$\dfrac{a_{n+1}}{2^{n+1}}=\dfrac{a_n}{2^n}+2$$

$$∴\quad \dfrac{a_n}{2^n}=\dfrac{a_3}{2^3}+2(n-3)$$

これを整理して， $a_n=(n+1)2^{n+1}$．

同様に $n$角形のときの$b$を$b_n$とする． $n=3$のとき， 左回りと決めると$b_3$も点の移動の順番の決め方は4通りある． 一つの移動の型に対し，Bのある辺は，一筆がきの最初と最後が辺を通り， 途中では弧を通ることが決まるので，$2^2$通りある． $b_3=2\cdot4\cdot2^2=32$である．

$n$角形に新たに$n+1$番の頂点を加えると， その頂点を挟むもとの$n$角形の2頂点の間の移動の仕方が， 2通りから4通りになる． これによって$n$角形の場合の一つの一筆がきの経路に対し， $n+1$角形の場合の一筆がきの経路が2つ得られる．

さらに新たに付け加わった$n+1$番目の点で折り返す一筆がきの経路が 右回りと左回りも考えて$2\cdot2^n$個できる． ゆえに

$$b_{n+1}=2b_n+2\cdot2^n$$

これから，$b_n=(n+1)2^n$．

吟味
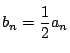$b_n$は解法1と同様に， $b_n=\dfrac{1}{2}a_n$となることを示す方が早いが， 漸化式ではどのようになるかを考えておいた． 数列を求めるときに漸化式が果たす役割は， いわゆる文章題で方程式が果たす役割に相等する．