問題
![]() ,
,![]() は自然数で,
は自然数で,![]() ,
,![]() を満たすものとする.いま,
を満たすものとする.いま,
![]() 角柱の
角柱の ![]() 個の面に 1 から
個の面に 1 から ![]() までの番号が書いてあるものとする.
この
までの番号が書いてあるものとする.
この ![]() 個の面に 1 面 ずつ,異なる
個の面に 1 面 ずつ,異なる ![]() 色の中から 1 色ずつ選んでは塗
っていく.このとき,どの隣り合う面の組も同一色では塗られない塗り方の数を
色の中から 1 色ずつ選んでは塗
っていく.このとき,どの隣り合う面の組も同一色では塗られない塗り方の数を
![]() で表す.
で表す.
方針
解1
(1)
![]() のとき.
ひとつの頂点に少なくとも3つの面がよるので,2色で塗ることは出来ない.
のとき.
ひとつの頂点に少なくとも3つの面がよるので,2色で塗ることは出来ない.
![]() のとき.底に3通りの選択で1色使う.側面は2色でぬらなければならない.
交互に塗るしかない.
のとき.底に3通りの選択で1色使う.側面は2色でぬらなければならない.
交互に塗るしかない.![]() が奇数なら
が奇数なら![]() の面と1の面が同色になる.
よって側面を2色で塗ることは出来ない.
の面と1の面が同色になる.
よって側面を2色で塗ることは出来ない.
![]() が偶数なら,底と側面は1を塗る色を決めれば,すべてきまる.
が偶数なら,底と側面は1を塗る色を決めれば,すべてきまる.

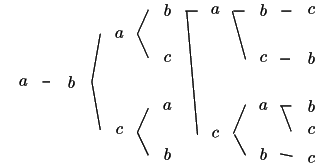
最初に塗る色![]() は7番目には塗れない.
は7番目には塗れない.
5番目に![]() 以外の色を塗れば6,7番の塗り方は3通り,
5番目に
以外の色を塗れば6,7番の塗り方は3通り,
5番目に![]() を塗れば6,7番の塗り方は2通り.
よって,
4番目に
を塗れば6,7番の塗り方は2通り.
よって,
4番目に![]() 以外の色を塗ればその後の塗り方が5通りあり,
4番目に
以外の色を塗ればその後の塗り方が5通りあり,
4番目に![]() を塗ればその後の塗り方が6通りとなる.
を塗ればその後の塗り方が6通りとなる.
あわせて21通りの型がある.
底の色を含めた4色の配置は![]() 通りある.
よって
通りある.
よって![]() のとき
のとき
訂正:「P4=4a3(n)」→「P4=4a3(7)」
![]()
![]()
![]() 次: 回数と確率[08京大理系甲乙]
上: 直接計算か漸化式か
前: 一筆がき[08京大文系]
次: 回数と確率[08京大理系甲乙]
上: 直接計算か漸化式か
前: 一筆がき[08京大文系]