正四面体ABCDを考える.点Pは時刻0では頂点Aに位置し,1秒ごとにある頂点から他の3頂点のいずれかに,等しい確率で動くとする.このとき,時刻0から時刻![]() までの間に,4頂点A,B,C,Dのすべてに点Pが現れる確率を求めよ.ただし
までの間に,4頂点A,B,C,Dのすべてに点Pが現れる確率を求めよ.ただし![]() は1以上の整数とする.
は1以上の整数とする.
方針
解1
時刻0から時刻![]() までの間にBに現れない事象を
までの間にBに現れない事象を![]() のように表す.4頂点A,B,C,Dのすべてに点Pが現れる事象は事象
のように表す.4頂点A,B,C,Dのすべてに点Pが現れる事象は事象
![]() の余事象である.
の余事象である.
事象![]() は点A,C,Dの間を動く事象,
事象
は点A,C,Dの間を動く事象,
事象
![]() は点A,Dの間を動く事象なので,
は点A,Dの間を動く事象なので,
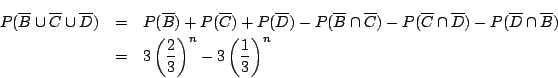
解2
時刻0から時刻![]() までの間に,
点Pが現れた頂点の個数が
までの間に,
点Pが現れた頂点の個数が![]() である状態を
である状態を![]() とおく.
とおく.
![]() のとき
のとき![]() であり,
4頂点A,B,C,Dのすべてに点Pが現れる確率は
であり,
4頂点A,B,C,Dのすべてに点Pが現れる確率は![]() である.
である.
![]() と
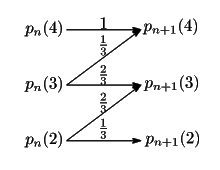
と![]() の間の推移の確率は図のようになる.
ただし状態を指示するところに確率を書きこんでいる.
の間の推移の確率は図のようになる.
ただし状態を指示するところに確率を書きこんでいる.
 これからまず
これからまず
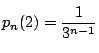 である.
次に
である.
次に
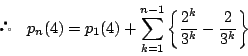
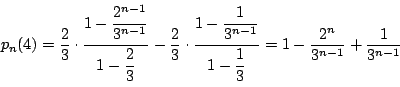
吟味

基本的にはすべての状態を数列に置き漸化式を立てることで解くことができる.