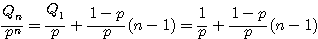![]() 平面上に
平面上に ![]() 個の点
個の点
![]() ,
,
![]() (
(![]() ,2,
,2,![]() ,
,![]() ) がある.
上下に隣り合う2点
) がある.
上下に隣り合う2点 ![]() ,
,![]() を結ぶ線分を「縦辺」(
を結ぶ線分を「縦辺」(![]() ,2,
,2,![]() ,
,![]() ),
左右に隣り合う2点
),
左右に隣り合う2点 ![]() ,
,
![]() および
および ![]() ,
,
![]() を結ぶ線分を「横辺」(
を結ぶ線分を「横辺」(![]() ,2,
,2,![]() ,
,![]() ) と言う.
すべての横辺には,各辺独立に,確率
) と言う.
すべての横辺には,各辺独立に,確率 ![]() で右向きの矢印が,
確率
で右向きの矢印が,
確率 ![]() で
で ![]() 印が描かれている.
またすべての縦辺には常に上向きの矢印が描かれている.
印が描かれている.
またすべての縦辺には常に上向きの矢印が描かれている.
このとき点
![]() から出発して,矢印の描かれている辺だけを通り,矢印の方向に進んで,
点
から出発して,矢印の描かれている辺だけを通り,矢印の方向に進んで,
点
![]() に到達する経路が少なくとも1本存在する確率
に到達する経路が少なくとも1本存在する確率![]() を求めよ.
を求めよ.
方針
解1
辺
![]() で最後の
で最後の![]() の位置で場合に分ける.ただし
の位置で場合に分ける.ただし![]() がない場合も考える.
がない場合も考える.
![]() に対してそれぞれ排反であるから,この場合の確率は
に対してそれぞれ排反であるから,この場合の確率は
![]() である.
である.
解2
![]() と
と![]() の漸化式を求める.
の漸化式を求める.
![]() までの点が合計
までの点が合計![]() 個あるとする.
点
個あるとする.
点
![]() から出発して点
から出発して点
![]() への経路が存在する場合を
2つに分ける.
への経路が存在する場合を
2つに分ける.