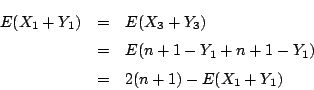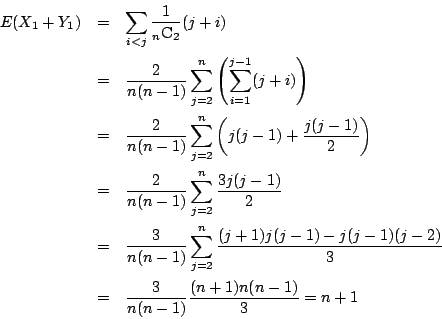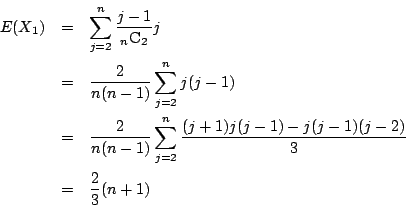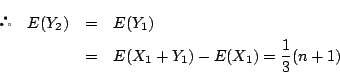次: 図形のとらえ方
上: 確率計算の方法
前: 確率変数の加法性[04年九大文理系]
次: 図形のとらえ方
上: 確率計算の方法
前: 確率変数の加法性[04年九大文理系]
問題
1 から  までの相異なる
までの相異なる  個の自然数(
個の自然数(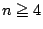 )の中から無作為に2 個を取り出し,
大きい方を
)の中から無作為に2 個を取り出し,
大きい方を 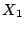 ,小さい方を
,小さい方を 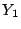 とする.
つぎに残りの
とする.
つぎに残りの 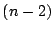 個の自然数の中から無作為に 2 個を取り出し,
大きい方を
個の自然数の中から無作為に 2 個を取り出し,
大きい方を 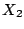 ,小さい方を
,小さい方を 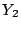 とする.
とする.
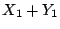 の期待値を求めよ.
の期待値を求めよ.
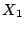 の期待値を求めよ.
の期待値を求めよ.
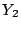 の期待値を求めよ.
の期待値を求めよ.
方針
- 1.
- 小問1を,確率分布が等しい確率変数の期待値は等しいことを用いる.
- 2.
- 小問1を計算で導く.
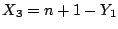 ,
, 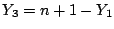 とおく.
とおく.
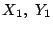 の確率分布と
の確率分布と
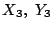 の確率分布は等しいから
の確率分布は等しいから
別解
-
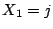 となるのは他の一枚が1から
となるのは他の一枚が1から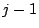 のいずれかのときである.
のいずれかのときである.
- 2回目に
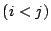 を引くのは,
1回目に
を引くのは,
1回目に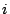 も
も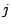 も引かず,2回目に残った
も引かず,2回目に残った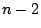 枚から
枚から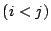 を引く場合であるから
その確率は
を引く場合であるから
その確率は
したがって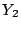 の確率分布と
の確率分布と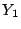 の確率分布は一致する.
の確率分布は一致する.
Aozora Gakuen
![]() までの相異なる
までの相異なる ![]() 個の自然数(
個の自然数(![]() )の中から無作為に2 個を取り出し,
大きい方を
)の中から無作為に2 個を取り出し,
大きい方を ![]() ,小さい方を
,小さい方を ![]() とする.
つぎに残りの
とする.
つぎに残りの ![]() 個の自然数の中から無作為に 2 個を取り出し,
大きい方を
個の自然数の中から無作為に 2 個を取り出し,
大きい方を ![]() ,小さい方を
,小さい方を ![]() とする.
とする.